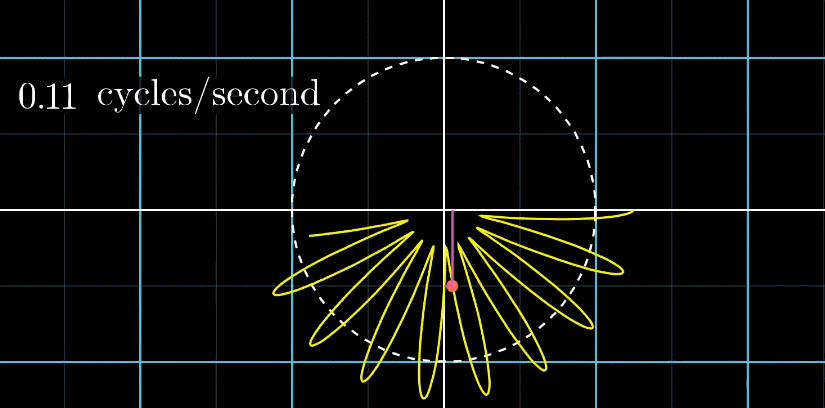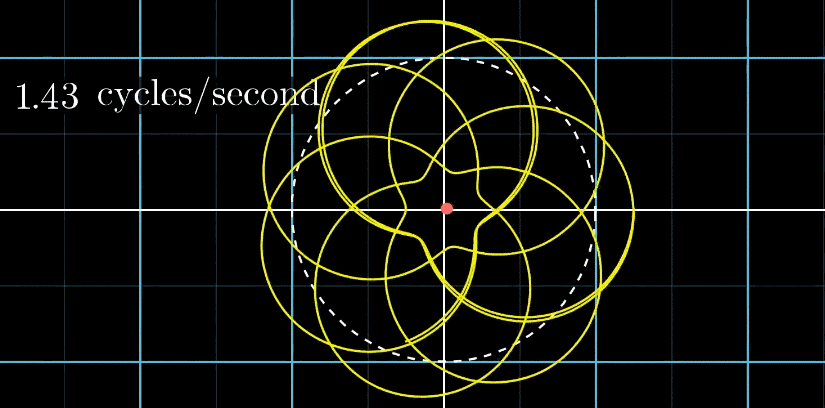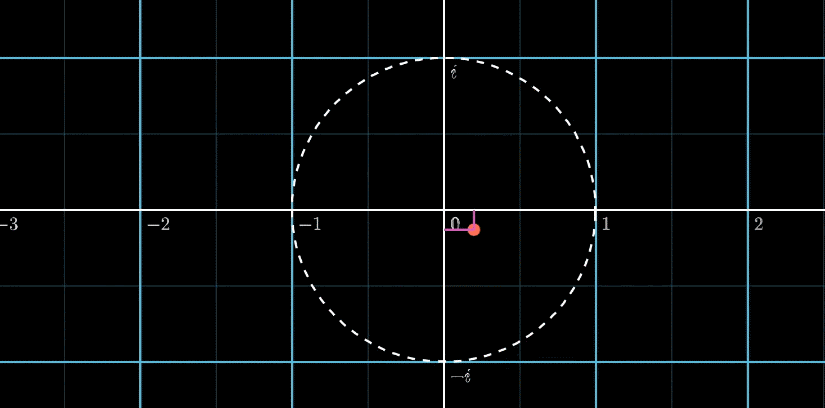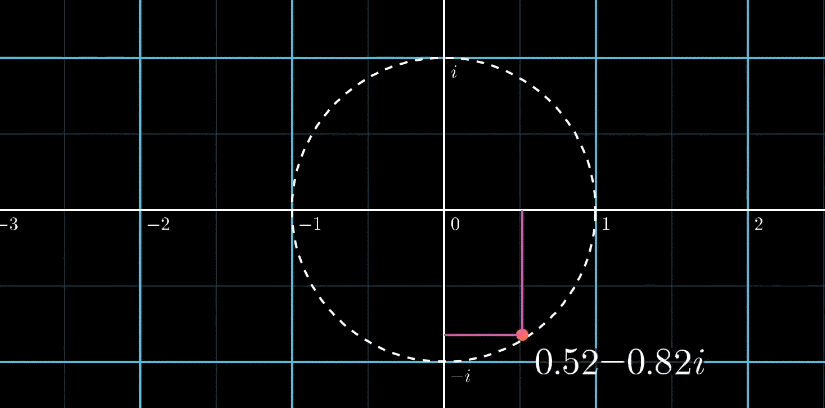
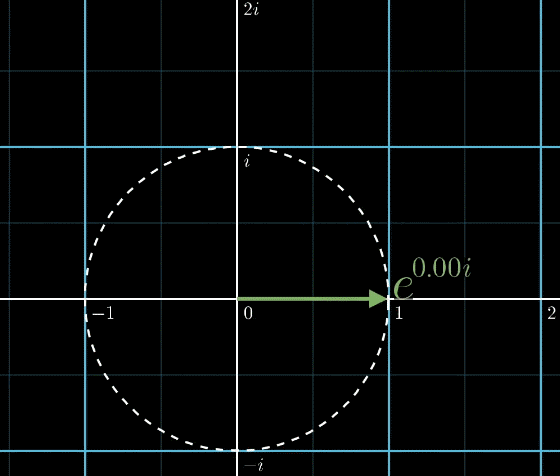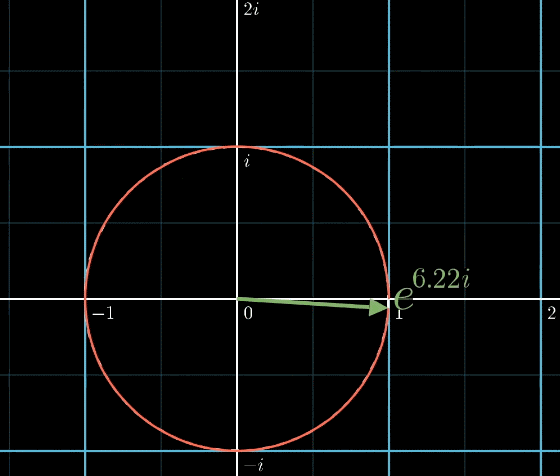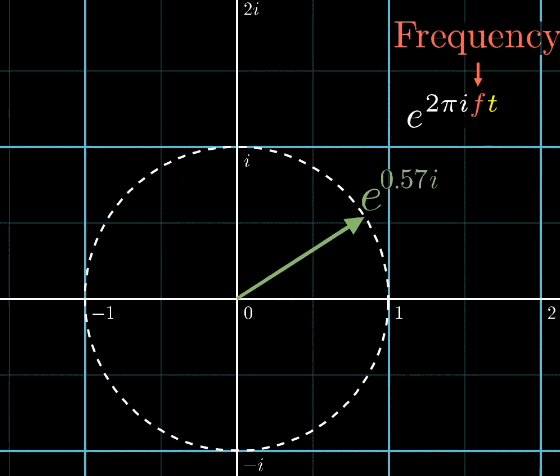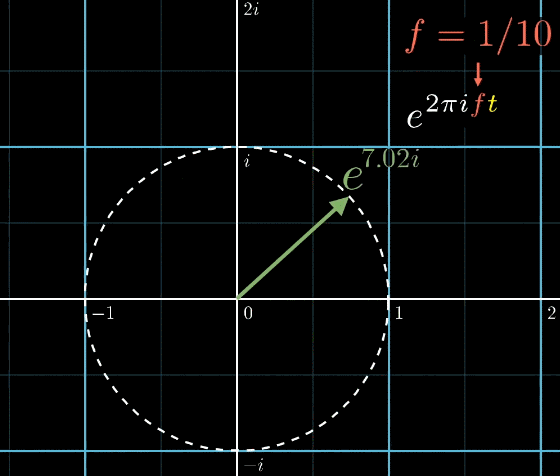
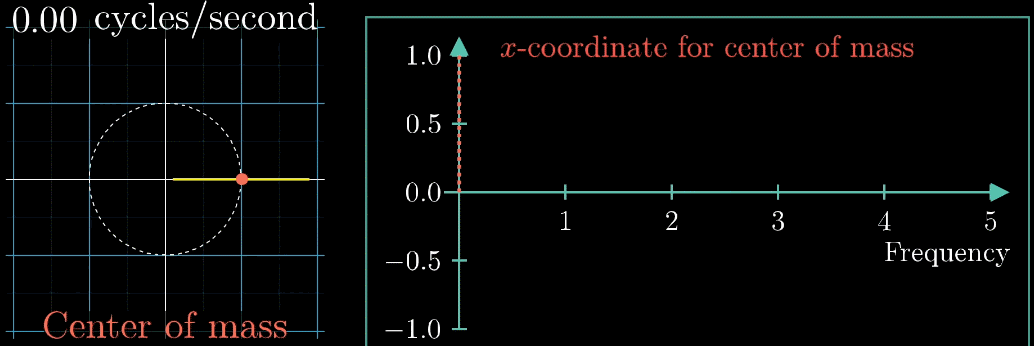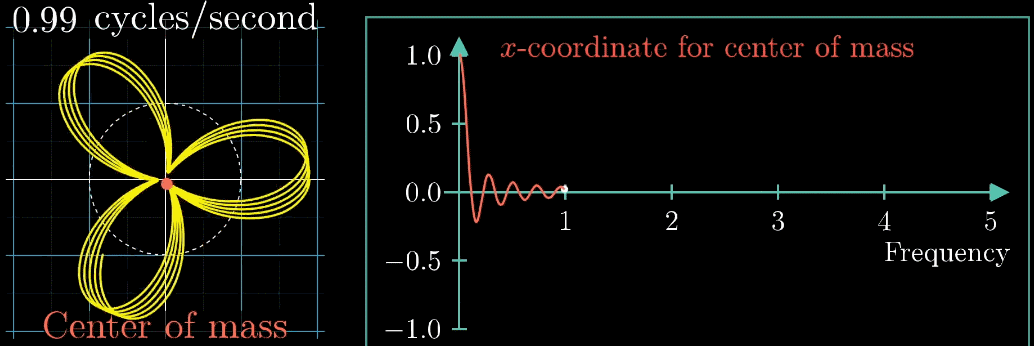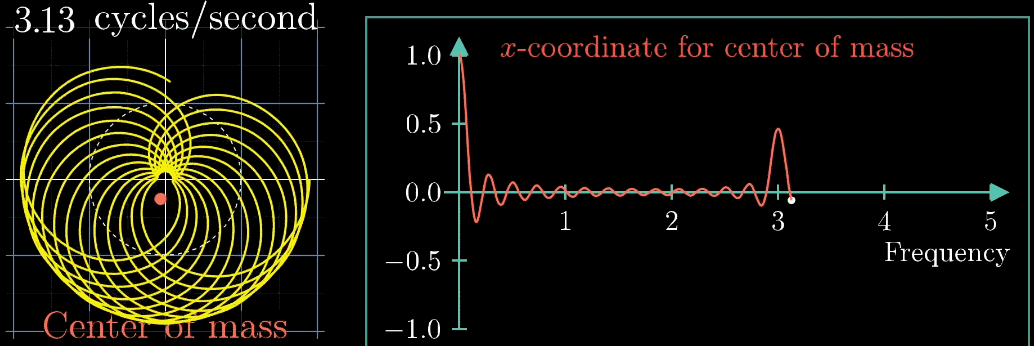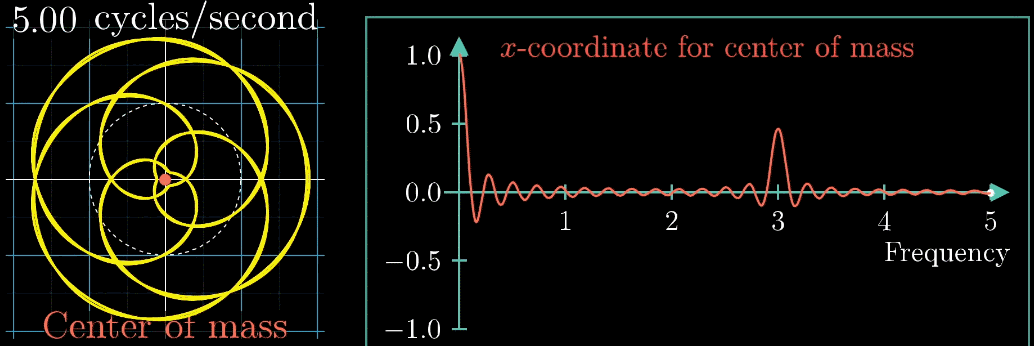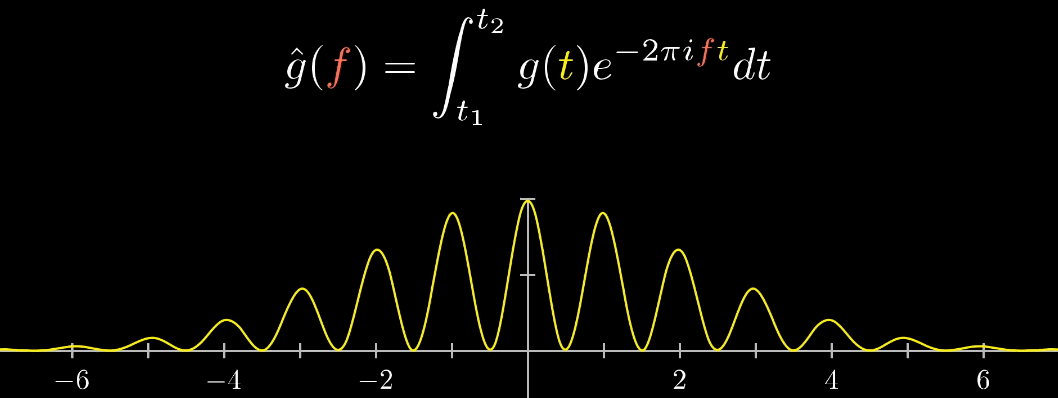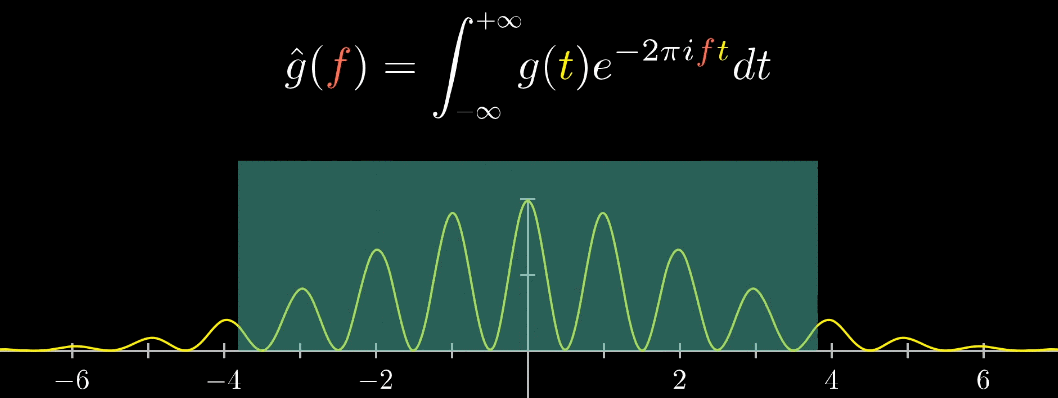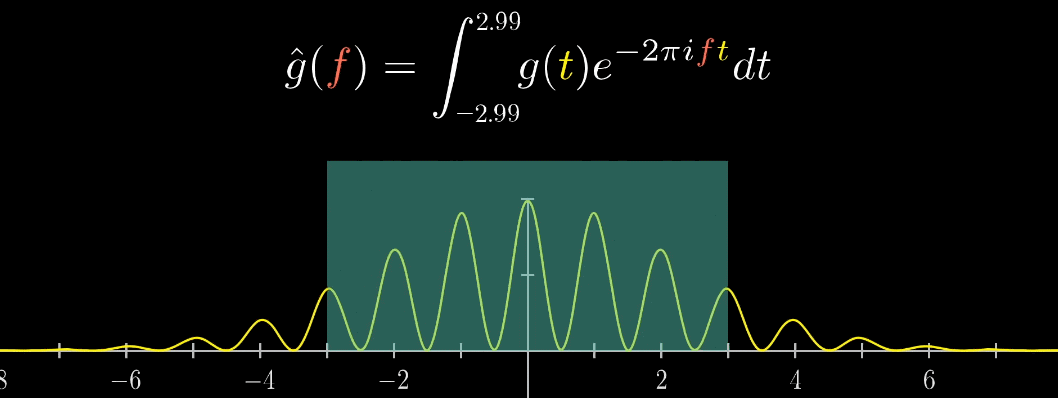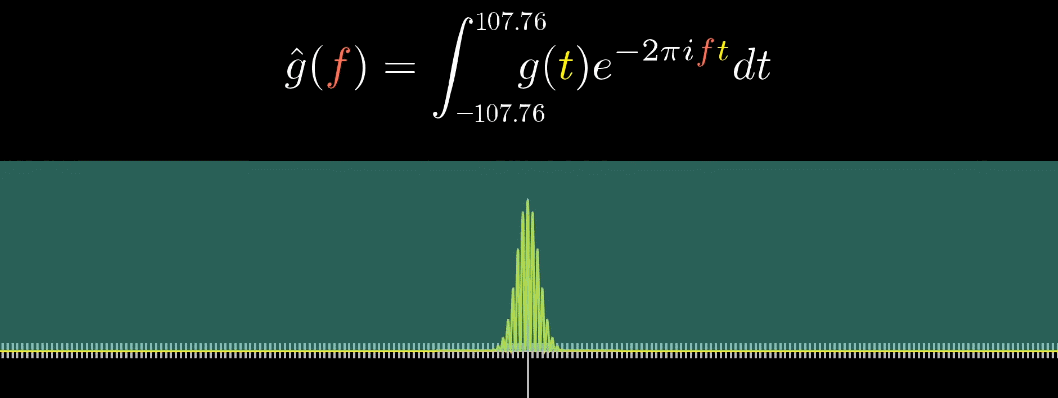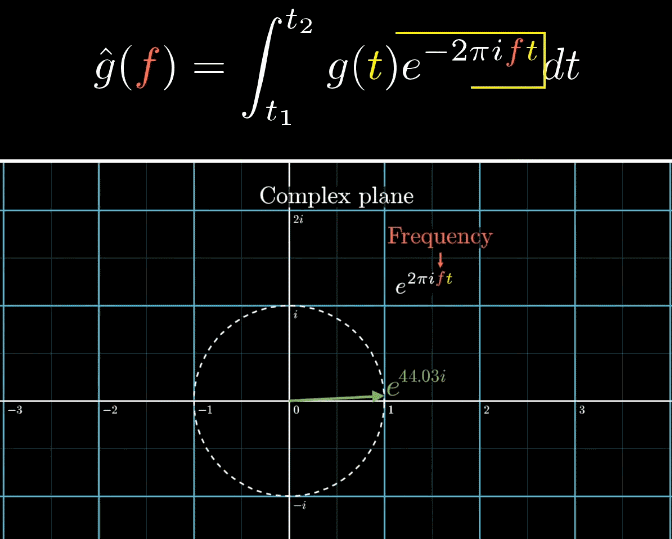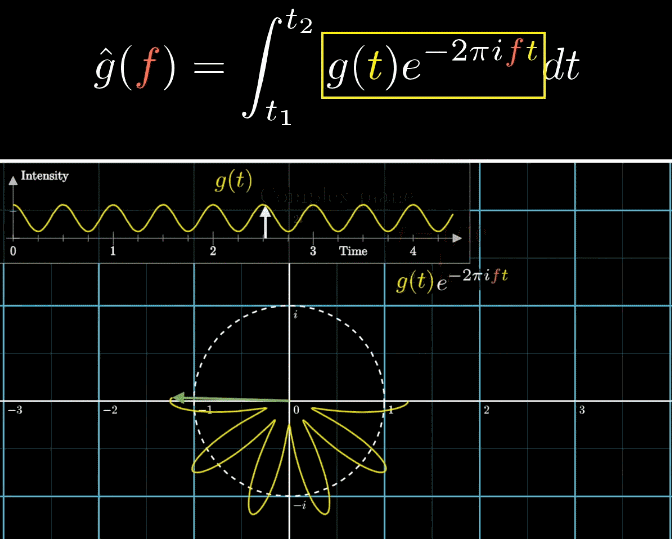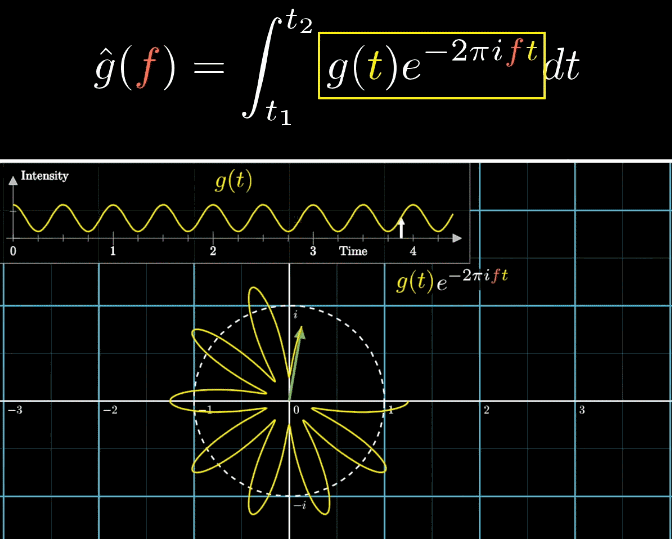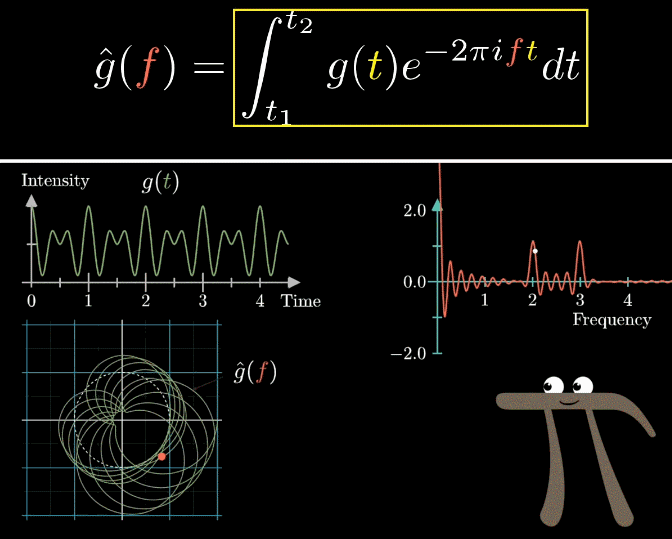But What's a convolution?

卷积

先提出了个投色子问题，投两次色子，两次色子的点数相加一共有多少种可能，每种可能对应的概率分为是多少？

下面是第一种可视化的方案，将两组色子按行、列进行组合，将一共得到36种结果，再将结果相同的点数进行累加

下面是第二种可视化的方案

将第二行的色子反转，对应位置与第一行的色子进行匹配，匹配结果：两行点数相加为7，并且一共有6种可能，$P(7)=6 \div 36$

而将第二行的色子左移，直到让第二行最后一个色子与第一行第一个色子匹配，匹配结果：两行点数相加为2，并且有1种可能

继续将第二行色子不断右移，则可以分别匹配到不同的相加后点数，以及对应的概率

---

然而，上面的概率是建立在每个色子都有相同的概率（1/6)基础上得到的，如果每个色子的概率不同呢？比如红色3的概率是0.24，而红色4的概率是0.1 ，如下图所示

那么，此时两组点数相加为3的概率就会发生变化，比如 $P(3)=0.16 \times 0.22 + 0.21 \times 0.11$

当然，计算的方式还是和之前相同的，只用把相加为3的两组色子的概率进行相乘，随后将相加数为3的很多概率相乘的结果再相加

---

将上面的概率抽像出来，第一组变成$a_1, a_2……$第二组变成$b_1,b_2……$

下面的同样如此

下面将引入“卷积”概念

$\begin{gathered}(a*b)_n=\sum_{i,j}a_i\cdot b_j\\i+j=n\end{gathered}$

---

下面是个举例，$(1,2,3)* (4,5,6)$，先将$(4,5,6)$反转，再逐个和$(1,2,3)$匹配相乘

如果使用python进行运算

import numpy as np
np.convolve((1,2,3),(4,5,6))
#将得到
array([4,13,28,27,18])

---

如果第一组很长，第二组很短，也可以进行计算

---

如果使用二维矩阵作为第二组，将图片作为第一组，那么可以得到**“模糊”**效果的结果图

如果放大来看，会发现第二组的矩阵，每个值都$1 / 9$，它代表将附近9个像素值进行加权运算，最终得到一个像素值

当然，如果原像素值是RGB（三通道），那么需要将三个通道中对应通道的值进行计算。

而将上述的行为，我们称作：卷积

---

高斯模糊图

如果“第二组”的矩阵分成$5 \times 5$的形式，而且，矩阵最中心的值是最大的，其它地方的值是离中心越远就越小，这样的数据分布特征是符合“高斯分布”

如果我们使用高斯分布矩阵对这$5 \times 5$格子内像素进行卷积操作，矩阵最中心的像素会有更大的权重，而越边缘的像素会有更小的权重，对原图进行这样的“高斯矩阵”卷积，将得到高斯模糊图

---

下面的矩阵更特殊，其左侧边缘为正权，右边缘为负权

如果对一张灰度图片进行操作（只有一个通道），比如下面的情况，最左边一列全黑（对应像素值为0），最右边一列全白（对应像素值为1），那么，对这片区域进行“卷积”操作后，会得到一个负值，我们将**“卷积”操作后的结果的“负值”**定义为红色，**结果的“正值”**定义为蓝色。

如果一片区域里面都是相同的颜色，那么这个区域进行“卷积”操作的结果就是“零”，非正非负定义成黑色

对整个图片进行了“卷积”操作后的结果如下图所示，可以看到，只有在边缘的地方才有颜色，而且左边缘是红色，右边缘是蓝色

那么，这种矩阵就可以用来找到图片的**“左右”边缘**（对图片是先从上到下逐个行，再对每行从左到右扫描）

---

如果将上面的矩阵进行调整，最上层是正权，最下层是负权，那么对图片卷积操作后，将得到**“上下”边缘的图**

其实，这个矩阵有个正式的名字：Kernel，核

---

卷积求解

快速卷积

fftconvolution(快速卷积)

虽然卷积的计算方法很简单，但是当x和h都很长的时候，卷积计算是非常耗费时间的。直接卷积运算的复杂度为$\mathcal{O}[N^2]$，因此有必要找到比直接计算卷积更快的办法。

举例：如下图所示，如果两个多项式都是有100项的系系数，如果通过相乘系数的方法来展开多项式，需要做10000次乘积计算，随后还需要“沿着对角线合并同类项”【卷积操作】，那么还需要10000次操作，于是直接卷积运算的复杂度为$\mathcal{O}[N^2]$

如果只考虑多项式的函数输出值，只对少数几个输入值进行采样计算，那么简洁运算的执行次数就等于样本数量。对于多项式来说，只需拥有N个函数输出值，就能确定(n-1)次多项式

比如，两个点（函数输出值）可以唯一确定一个一次多项式($a_0+a_1 \times x$)，三个点（函数输出值）可以唯一确定一个二次多项式($a_0+a_1 \times x +a_2 \times x^2$)，如果知道N个点（函数输出值），就可以唯一确定一个(N-1)次多项式。

假设目前有个多项式$h(x)=c_0+c_1x^1+c_2x^2+c_3x^3+c_4x^4+c_5x^5+c_6x^6+c_7x^7$，$h(x)$假设是$f(x) \times g(x)$的乘积结果，并且系数$c_i$都是未知量

假如，现在知道多项式的输出值，比如$h(1), h(2)…… h(x)$（可以通过$f(1) \times g(1)，f(2) \times g(2)……f(x) \times g(x)$求出来），而且提供了 与未知系数的个数相同数量的方程式，从原理上来说，这些方程式可以用来还原出来系数值

例如，现在有A(x)和B(x)两个多项式，而$C(x)=A(x) \times B(x)$，那么C(x)将是4维（degree 4)需要5个点才能唯一确定一个四维的多项式

所以，需要分别在A(x)和B(x)上取各自取5个点，将这5个点对应的函数值$A(x_i)、B(x_i)$相乘，从而得到$C(x_i), i \in {(0,4)}$，如下图所示

上面这小部分，讲述的是将通过A(x)和B(x)相乘(Mulitiply)得到C(x)，然后，这只是"快速卷积"中的一小步，如下图所示

然后，让我们看下宏观图（big piture），快速卷积的大致流程如下

1. 拥有两个多项式A(x)和B(x)
2. 将Coeff转成Value，这部分就是FFT
3. 对A(x)和B(x)使用相乘(Multiplay)操作得到C(x)的Value
4. 将C(x)从Value转成Coeff，从而得到具体的C(x)函数

---

时域的卷积等于频域的乘积这个定理，因此要计算时域的卷积，可以将时域信号转换为频域信号，进行乘积运算之后再将结果转换为时域信号，实现快速卷积。

经过优化的FFT其运算的复杂度为$\mathcal{O}[NlogN]$，显然通过FFT计算卷积要比直接计算快速得多。

不过由于FFT运算假设其所计算的信号为周期信号，因此通过FFT计算出的结果实际上是两个信号的循环卷积，而不是线性卷积。
使用numpy的fft来计算卷积：

import numpy as np

x = [5,6,7,8]
h = [1,2,3,4]

X = np.fft.rfft(x)
H = np.fft.rfft(h)
y = np.fft.irfft(X*H)

print('fft计算卷积结果为:')
print(y)
1234567891011

输出为：

fft计算卷积结果为:
[66. 68. 66. 60.]
12

可以看到，将x和h变换到频域相乘，然后变换回时域的结果与循环卷积的结果一致。
如果需要使用FFT计算线性卷积，就需要对信号进行补零扩展，使得其长度长于线性卷积结果的长度。
对x和h进行补零，然后再进行fft：

import numpy as np

x = [5,6,7,8]
h = [1,2,3,4]

X = np.fft.rfft(x,n=7)
H = np.fft.rfft(h,n=7)
y = np.fft.irfft(X*H,n=7)

print('fft计算卷积结果为:')
print(y)
1234567891011

输出为：

fft计算卷积结果为:
[ 5. 16. 34. 60. 61. 52. 32.]
12

可以看到，结果与线性卷积结果一致

傅里叶变换

傅里叶变换的核心，是“换个角度看待问题”

比如，对于一时间段内的声音信号，不是看每时每刻的强度，而是看信号内不同频率的强度

傅里叶变换FT（fourier transform）用于将时域信号x(t)和频域信号X(f)之间变换，公式如下所示：

$\hat{f}\left(\xi\right)=\int_{-\infty}^{\infty}f(x)e^{-2\pi ix\xi}dx\quad\xi\text{ 为任意实数}$

很多时候，这里的$\hat{f}\left(\xi\right)$会写成 $F(w)$或$F(f)$ 表示角速度或者频率，当然后面的公式的量纲也需要对应的修改；后面的自变量 x大多数时候都是写成t表示时间。当然，他们表示的都是同一个东西

联想链条

既然是为了【理解】和【记忆】，那么我们还是需要定义一个联想链条：

傅立叶变换 ➜ 分解声音的过程

建议使用分解声音这个例子来理解傅立叶变换，非常好用

声音的表示

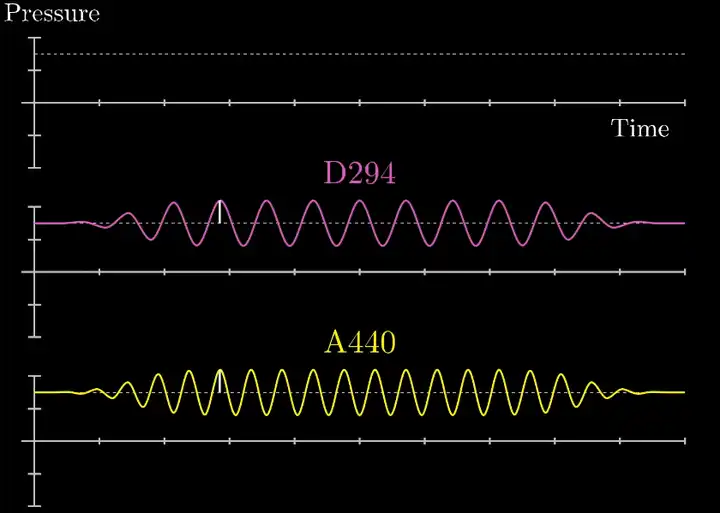
我们是如何记录声音的呢？如果你测量的是扬声器旁的气压，那么它会是一个随时间以正弦函数形态不断震荡的图像。

一个标准音 A（下图黄色），它的频率是440Hz，表示每秒钟振动440次

一个比标准音 A 低一些的 D（下图紫红），它的频率是294Hz，表示每秒钟振动294次，振动的慢一些。

如果这两个音同时发出，产生的气压随时间曲线怎么决定呢？如下动图，其实就是把所有时间点的振幅加起来，下图中最上层的一条曲线

那么如果给你随意一段随时间变化的气压曲线，你如何找到这些原有的组成音符呢？这就是我们的目的，参考下面的动图，感觉有点像是把一盘混好的原料分成组成它的单独的颜色，感觉不那么容易吧？

下面就需要一步一步把这件事情做出来

可视化方法

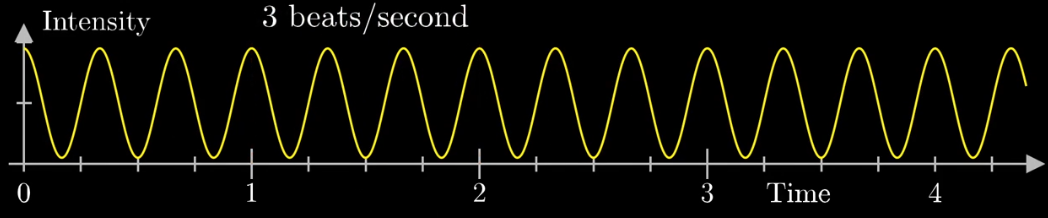
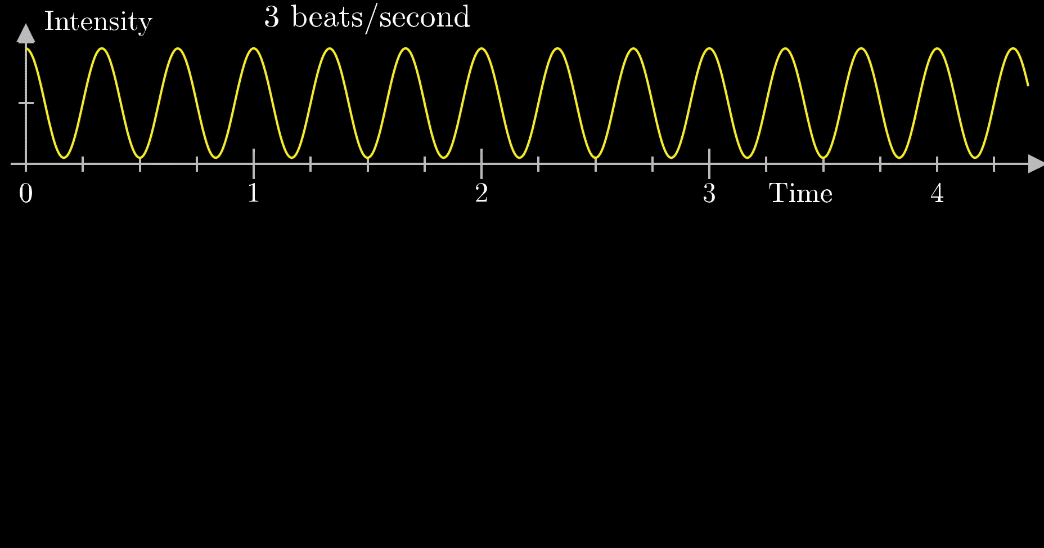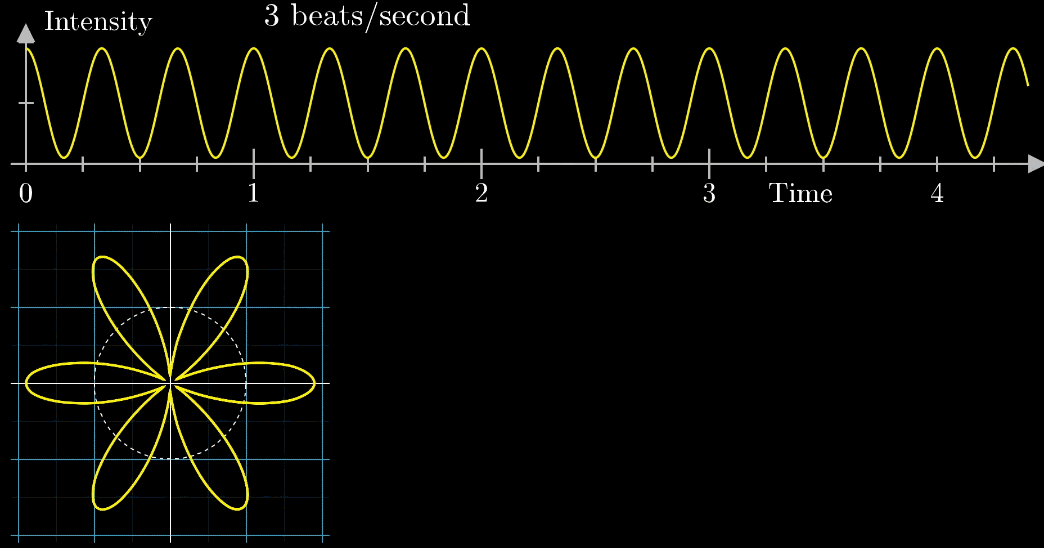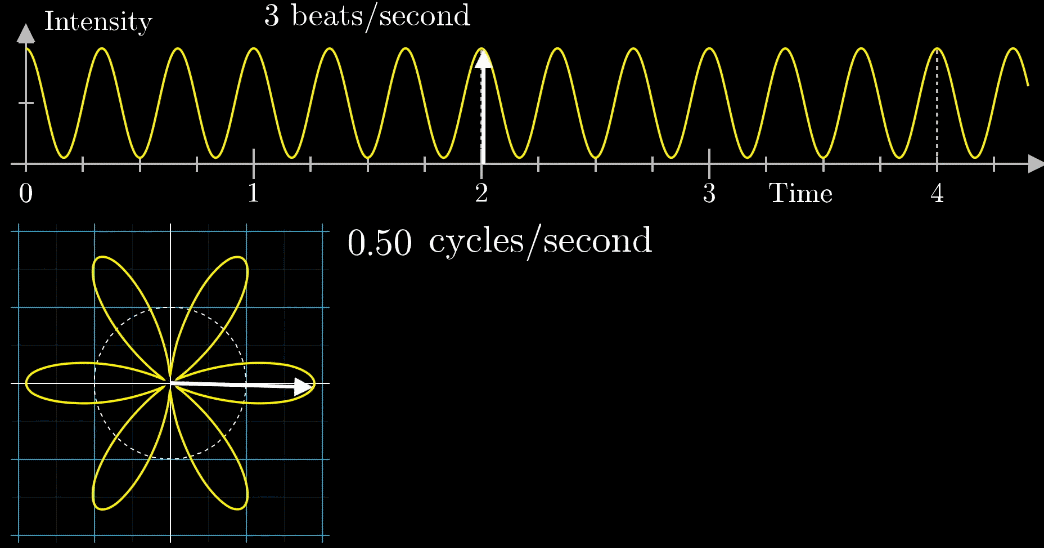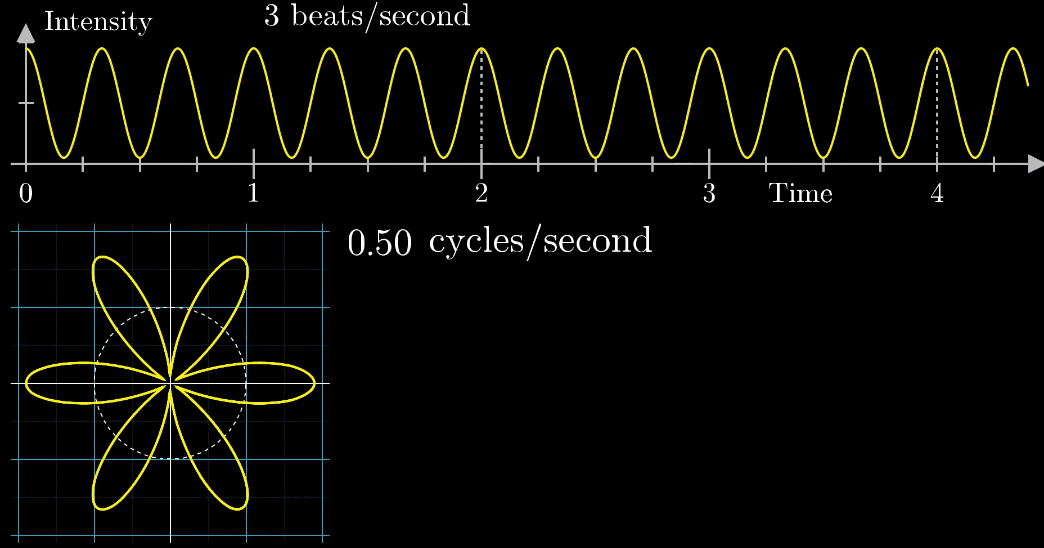
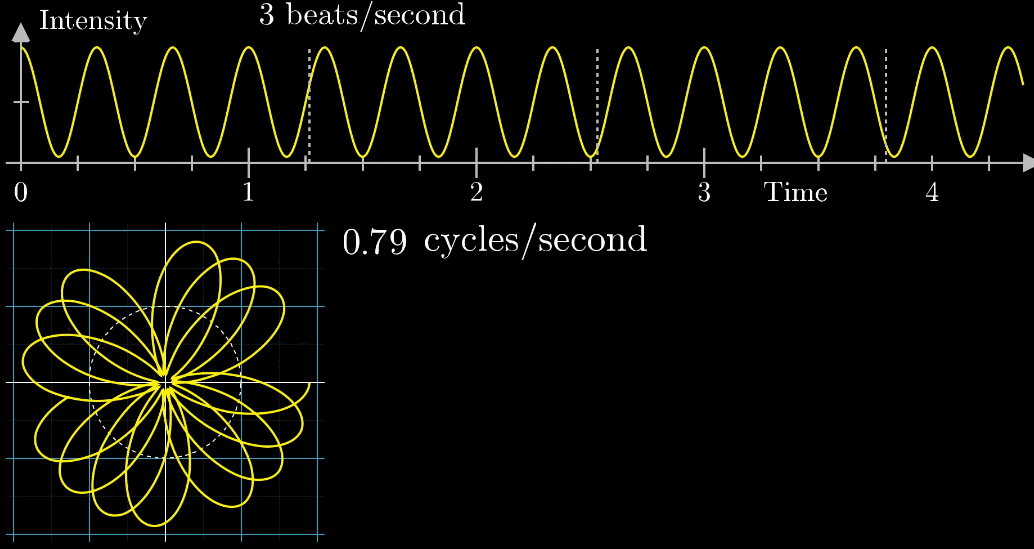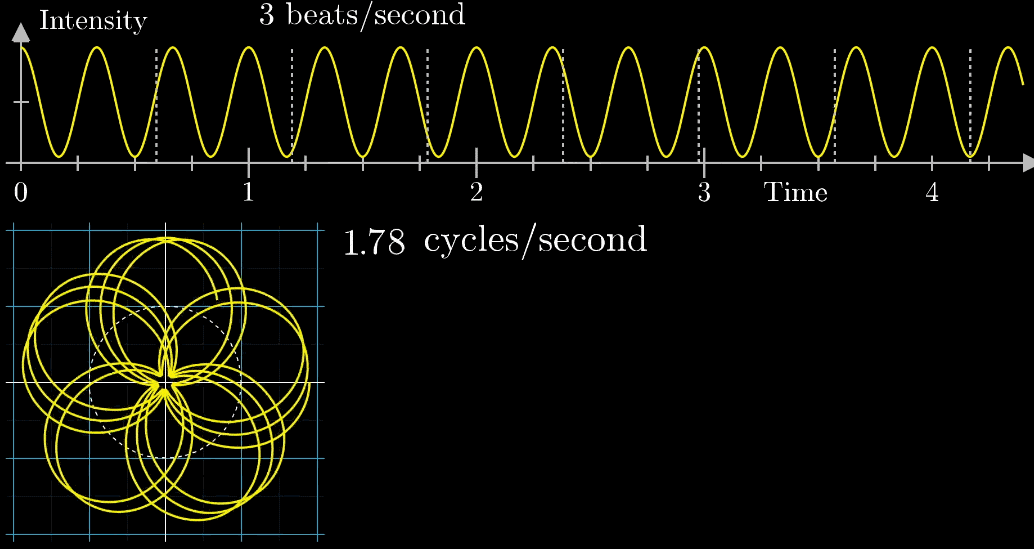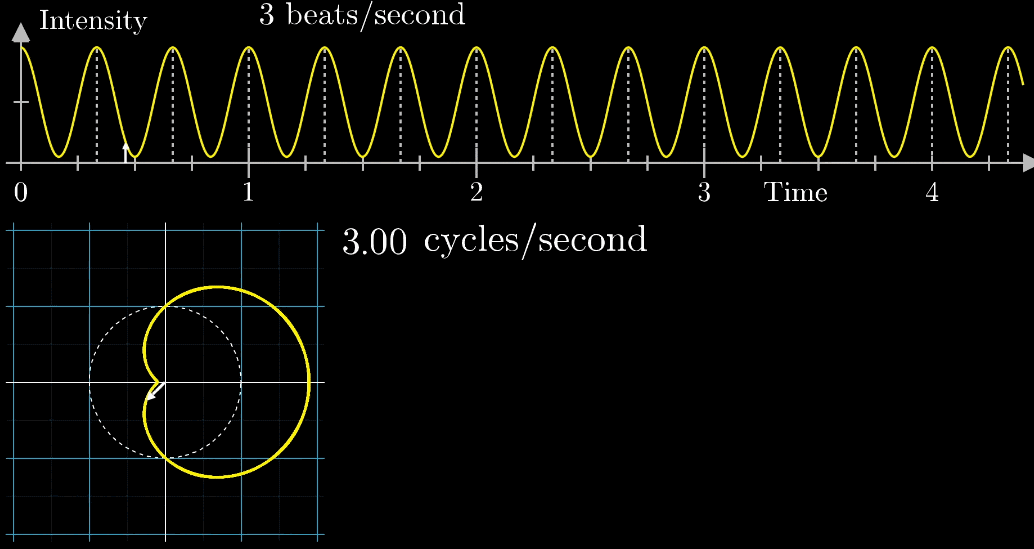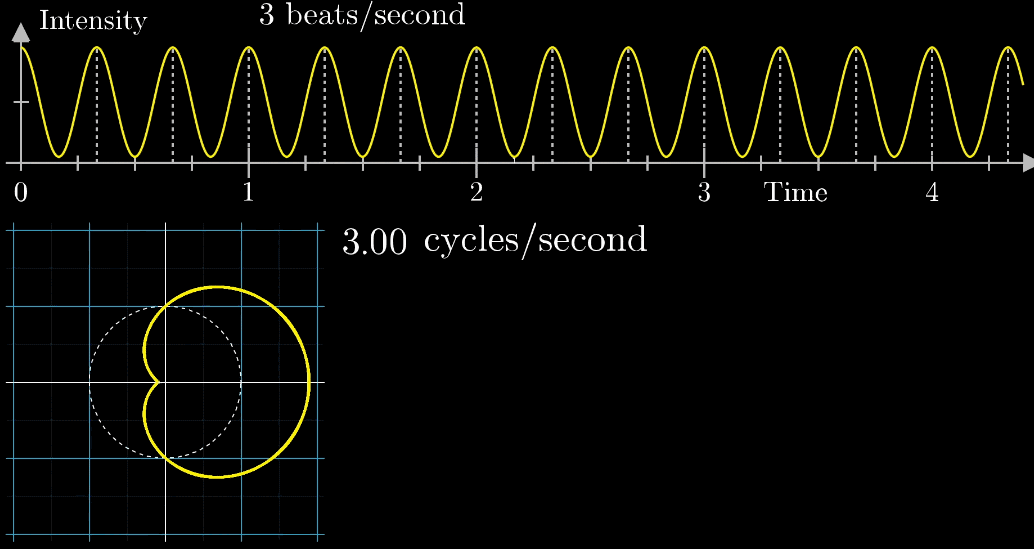
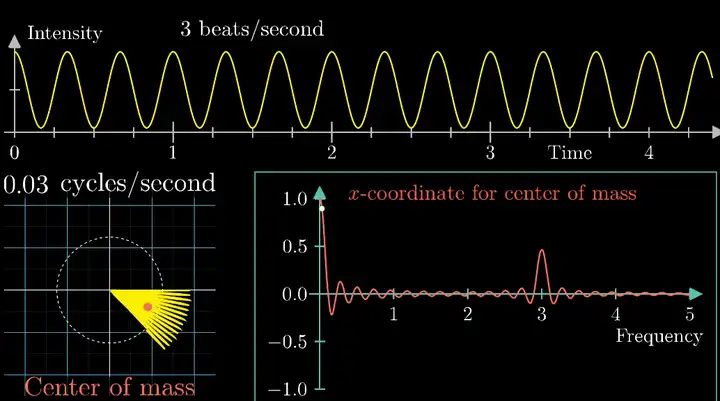
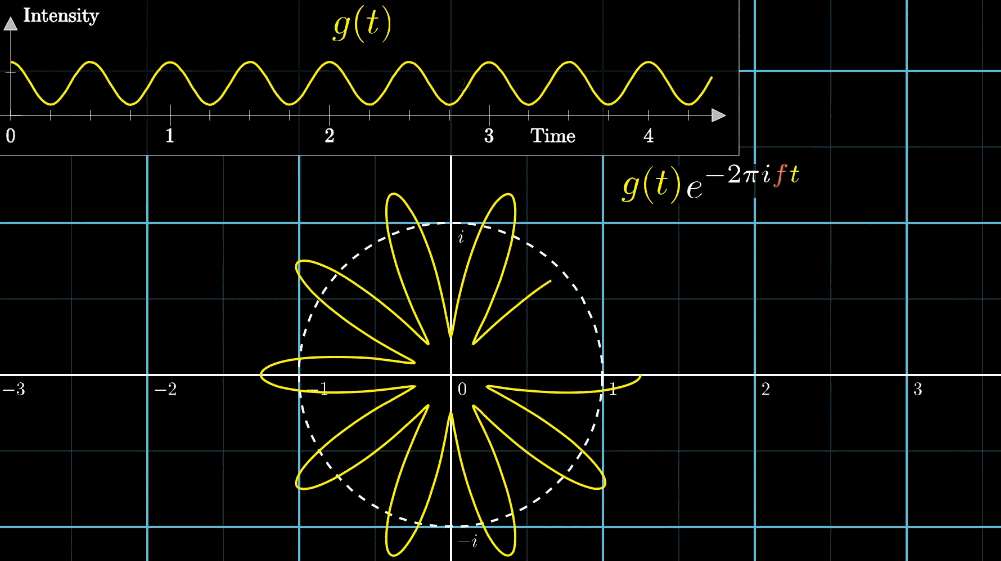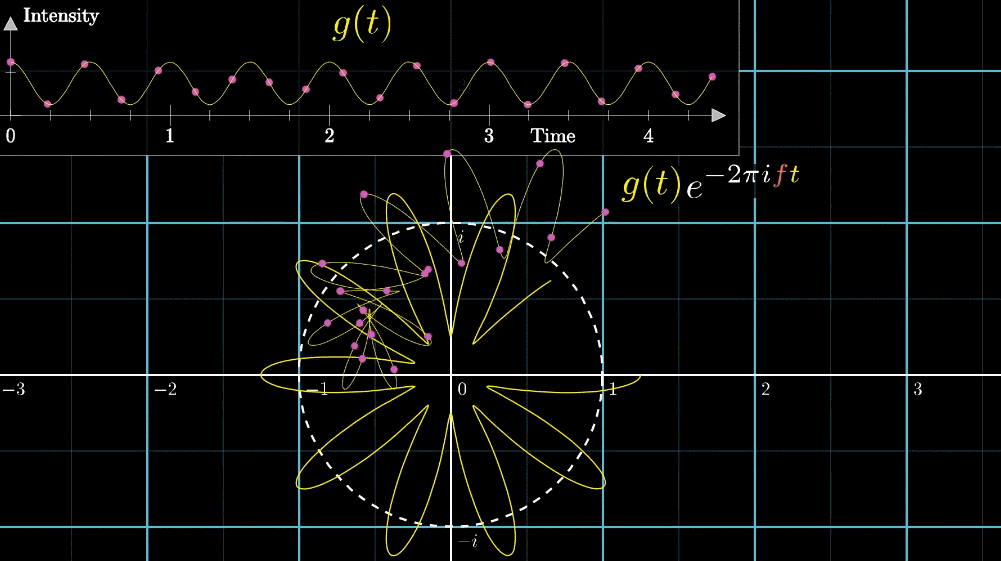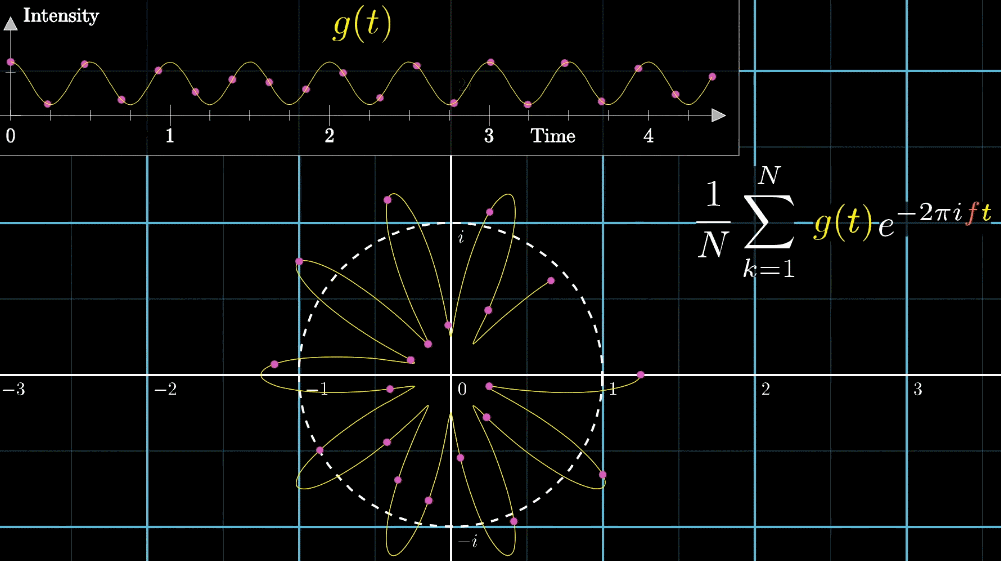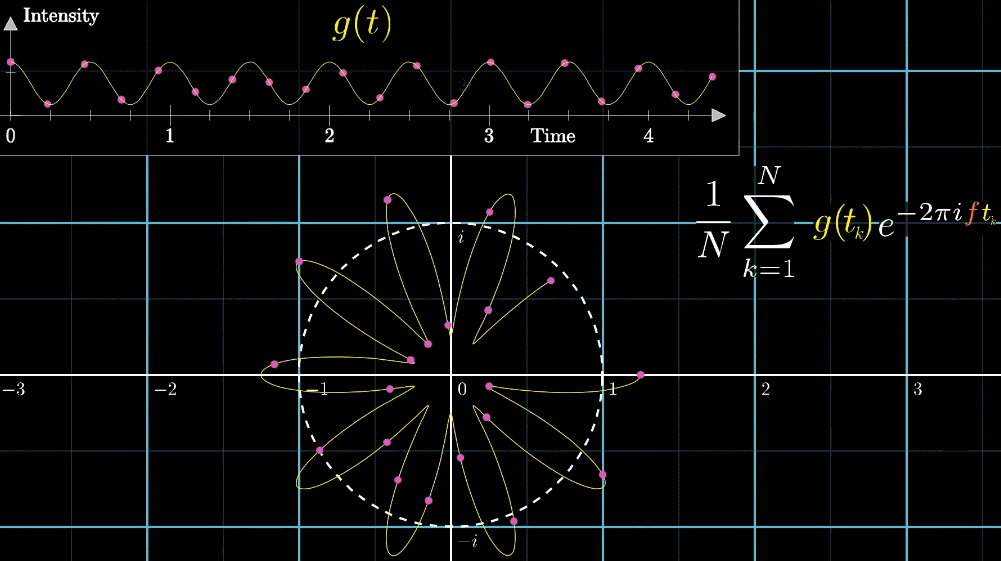
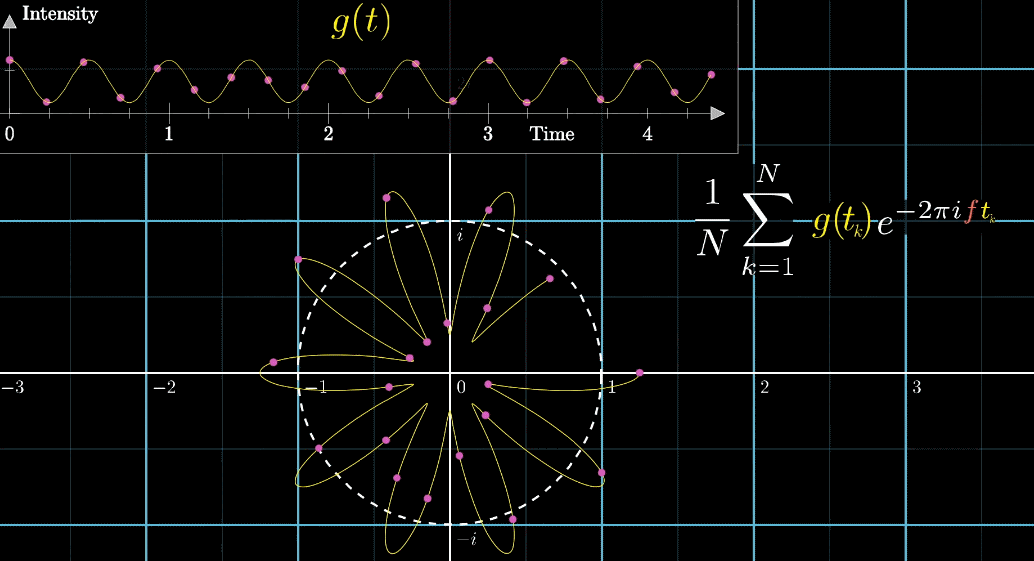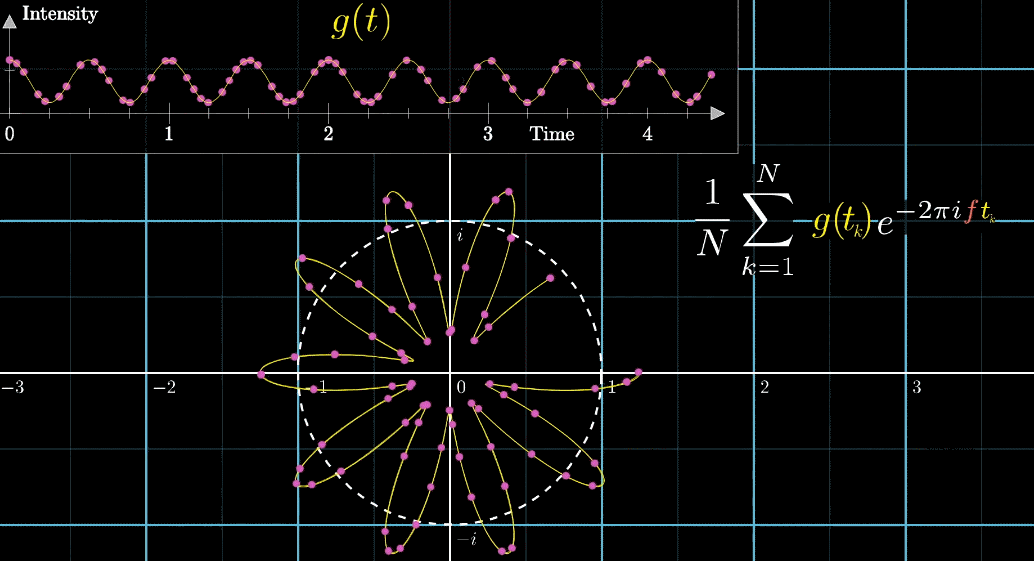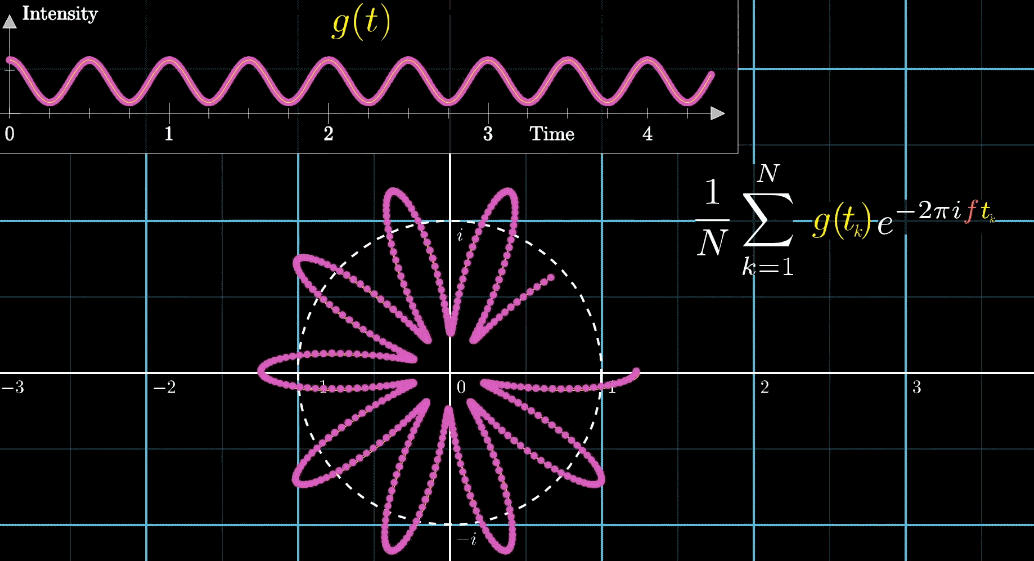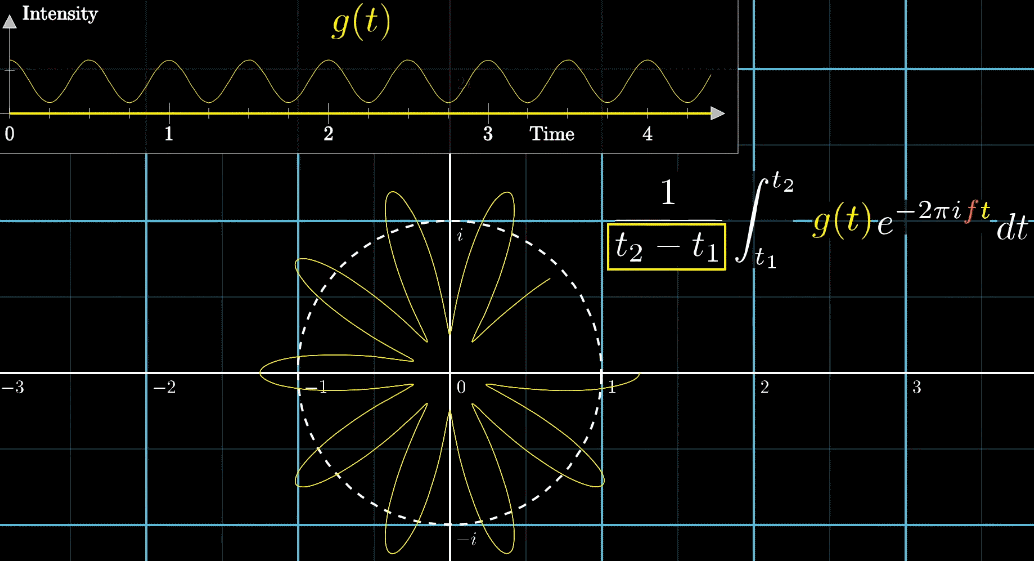
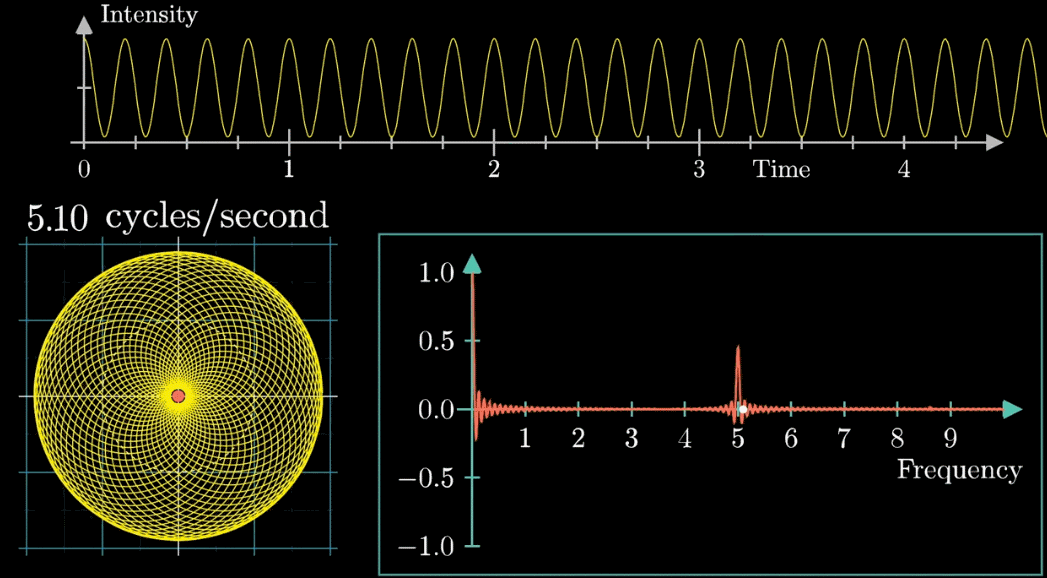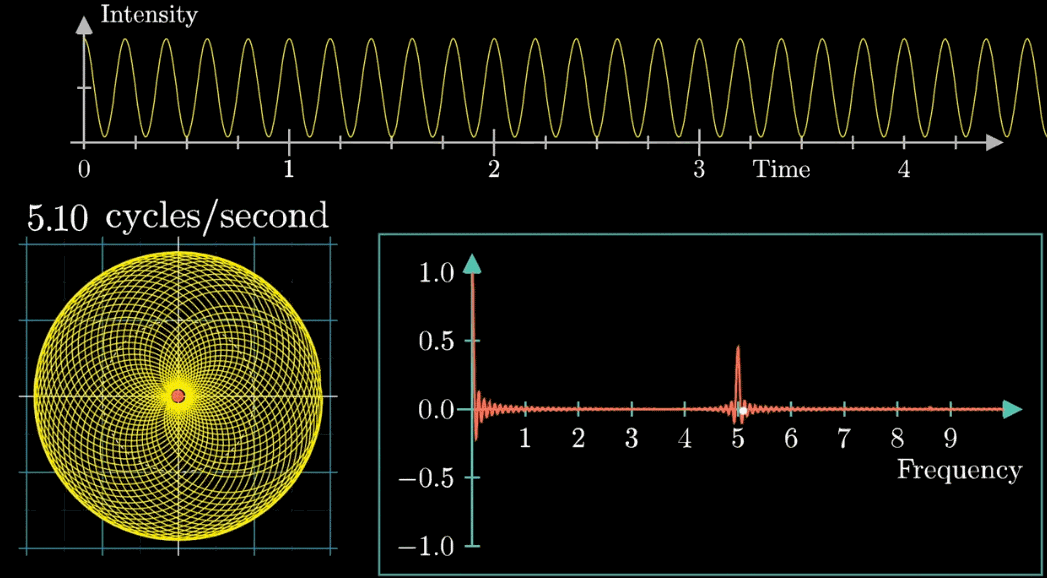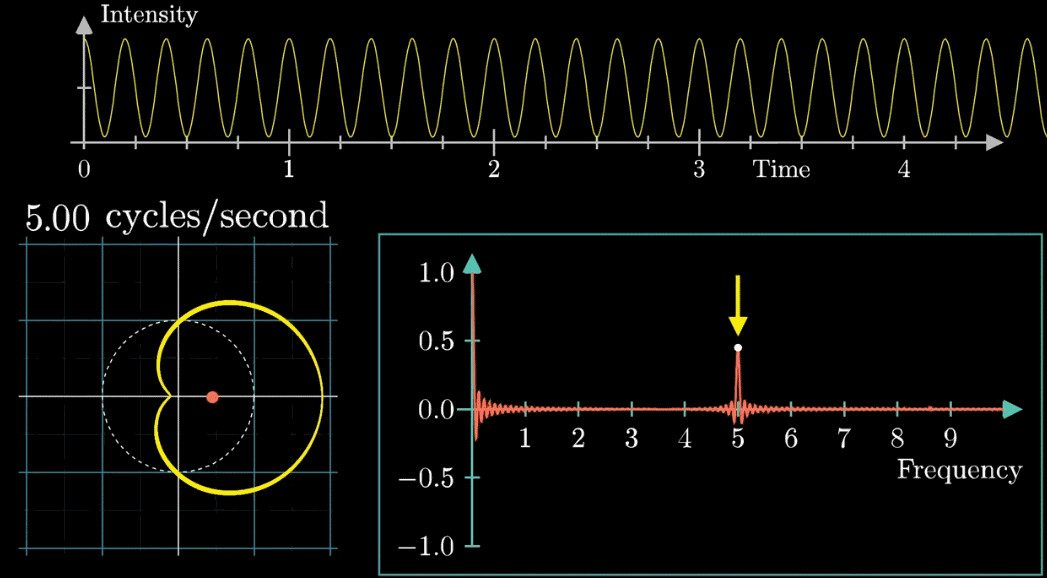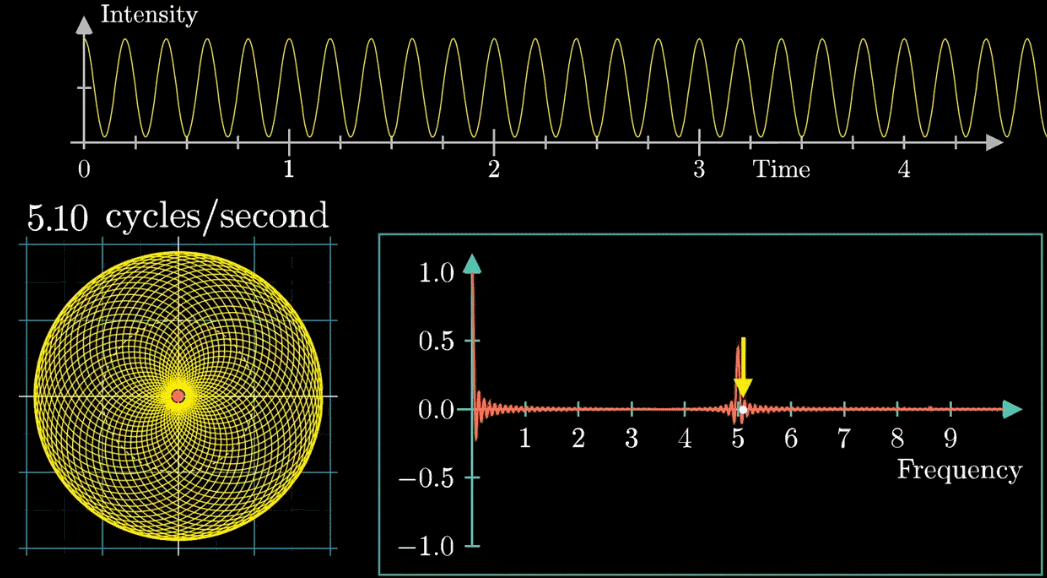
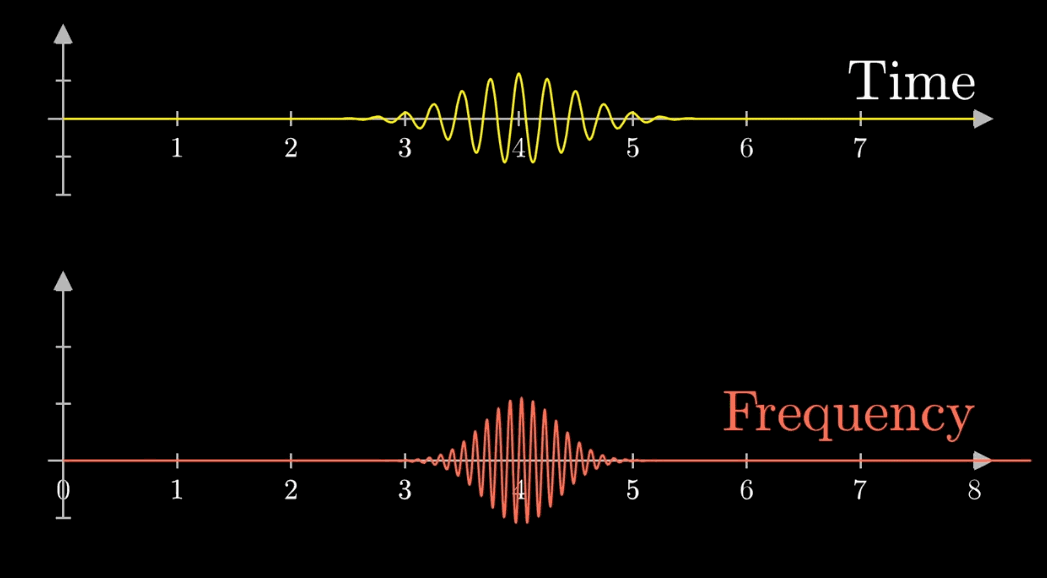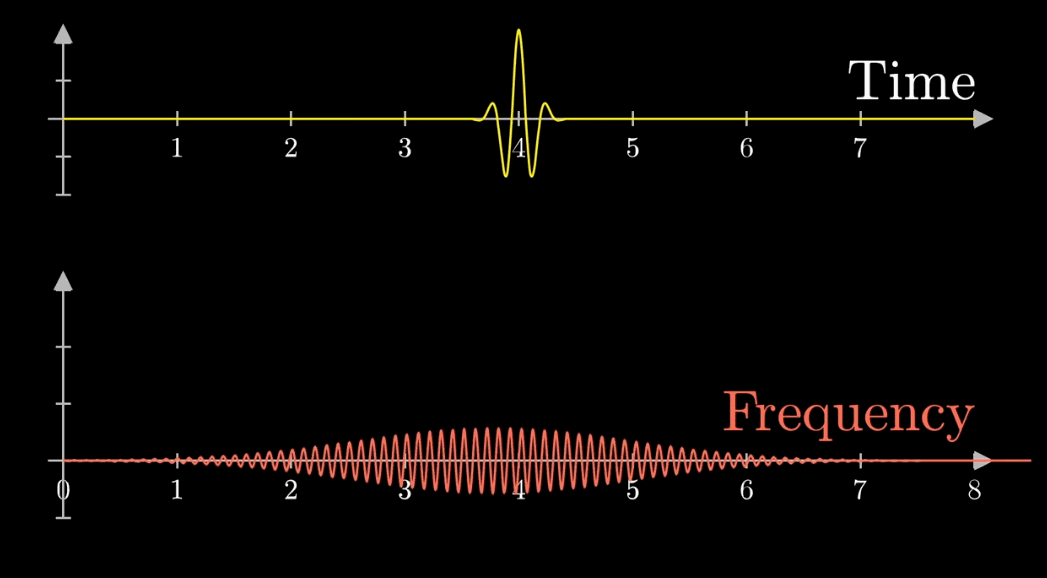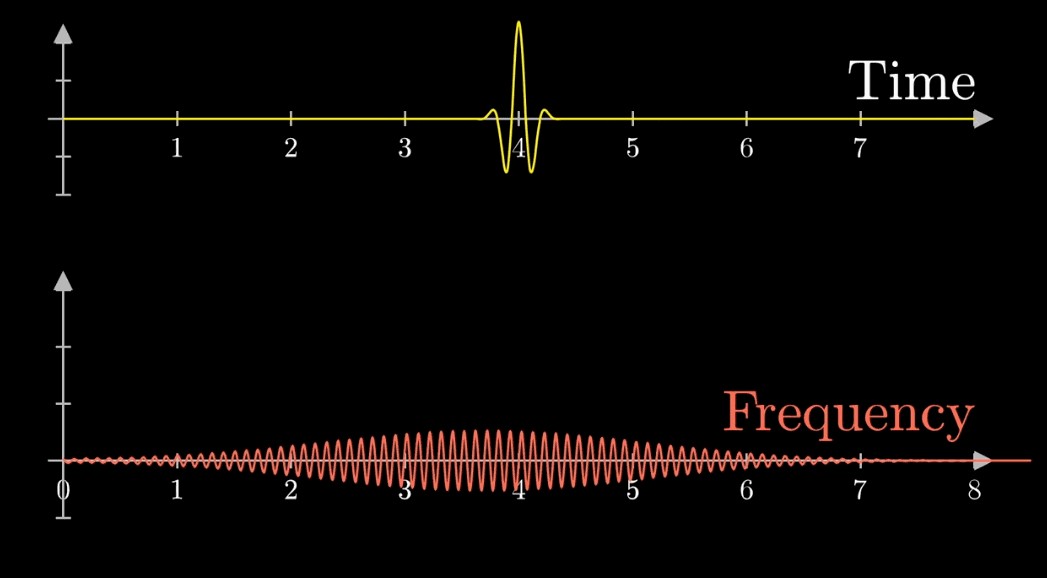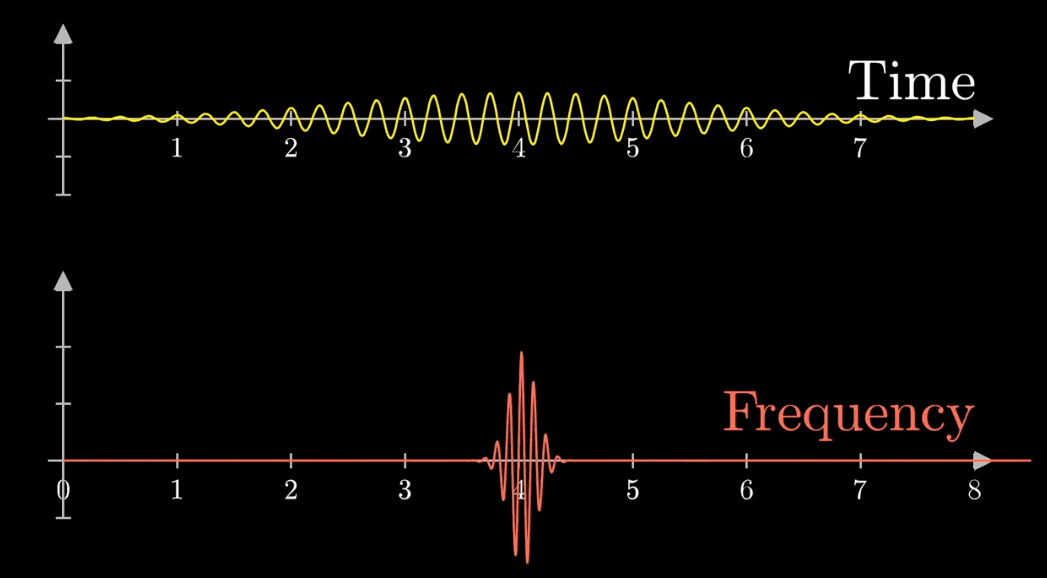
首先，假设我们有一个每秒钟振动3次的声音信号（440Hz实在太快啦），它的图像如下（Intensity为强度，可以同理成气压），并且，我们只关注前面的4.5秒（即图像中画出来的部分）

绕圈记录法：同一事物的不同角度

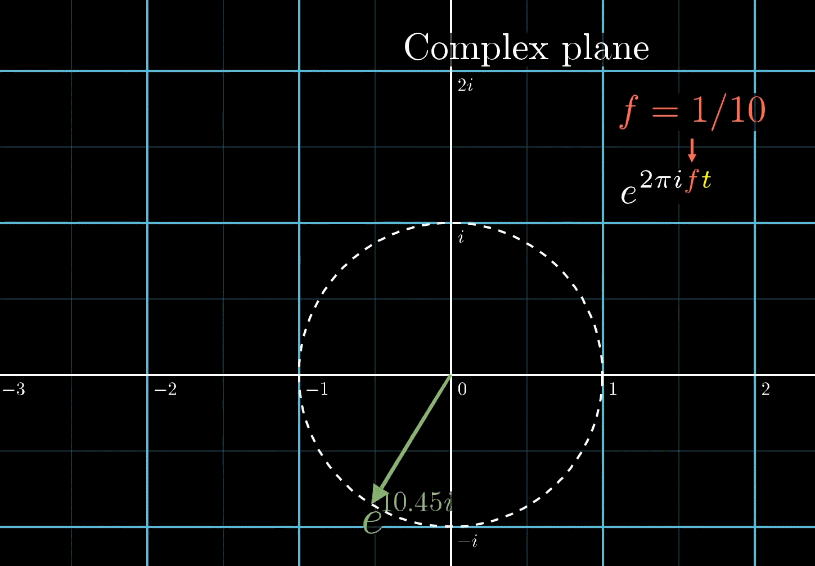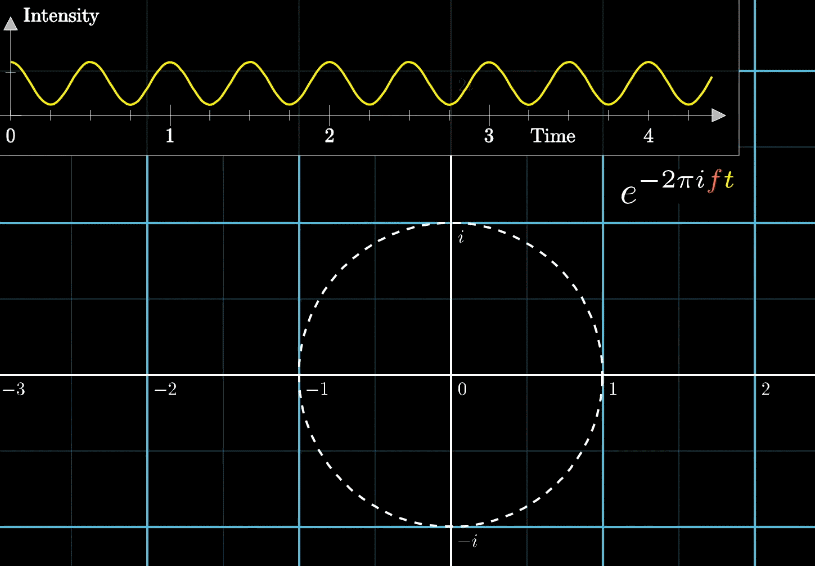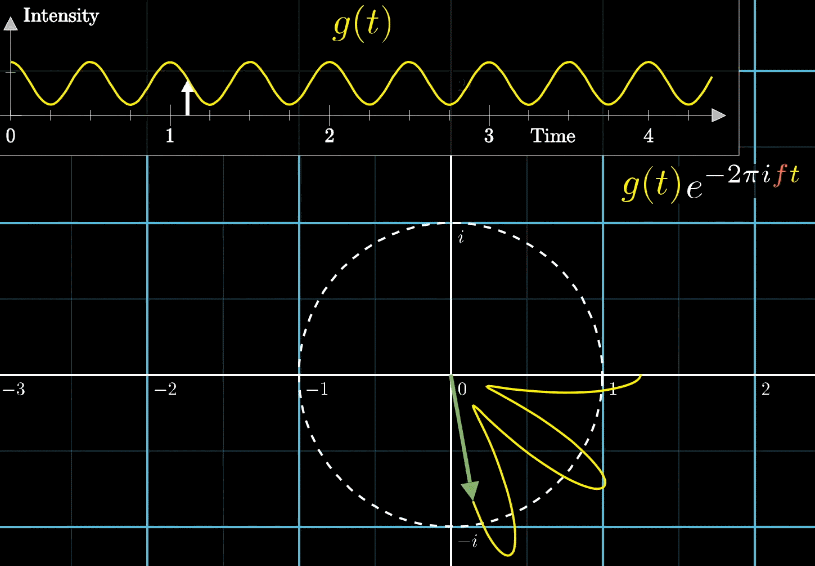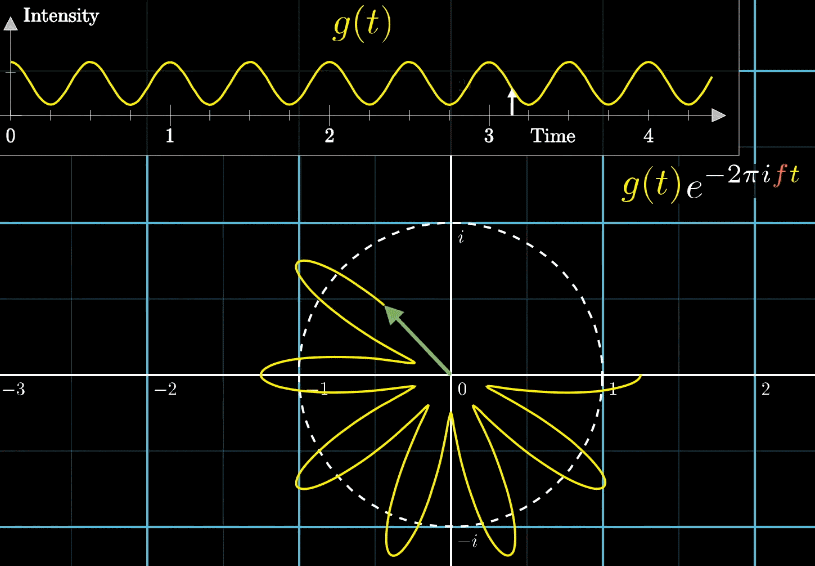
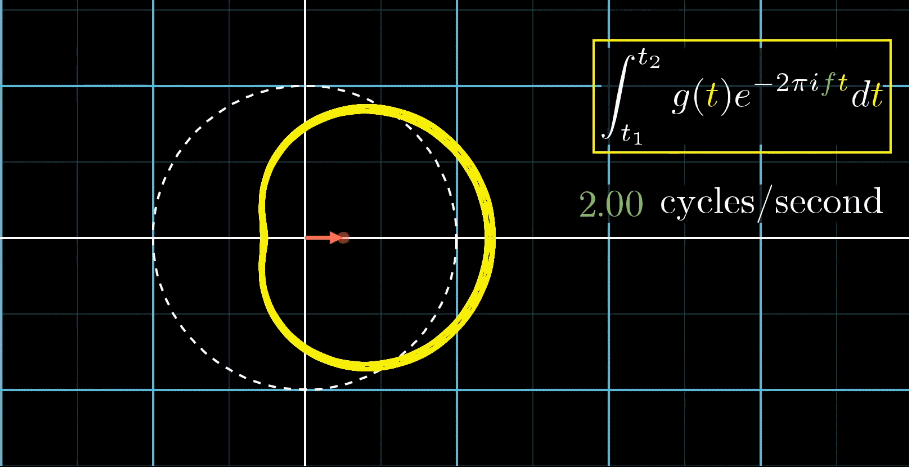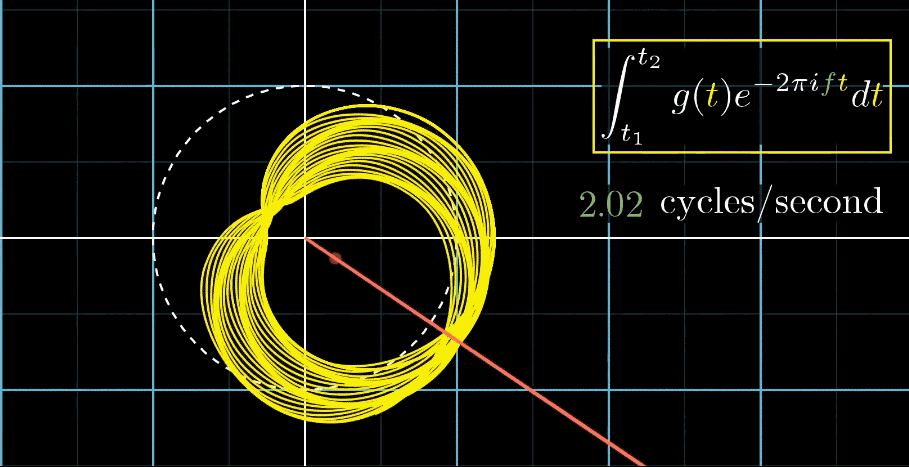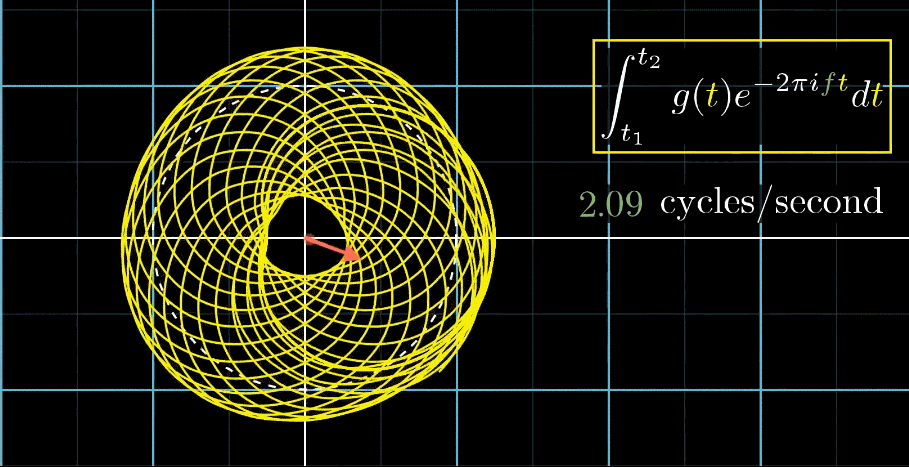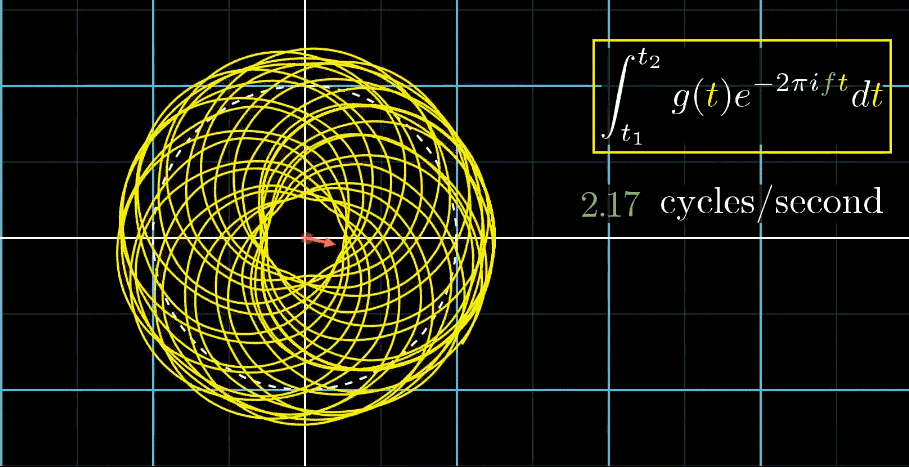
千万不要眨眼！下面是最关键的一步，是【看到】傅立叶变换的核心部分，如下面动图所示

• 首先把黄色曲线缠绕到一个圆上，大小就是原本信号的振幅
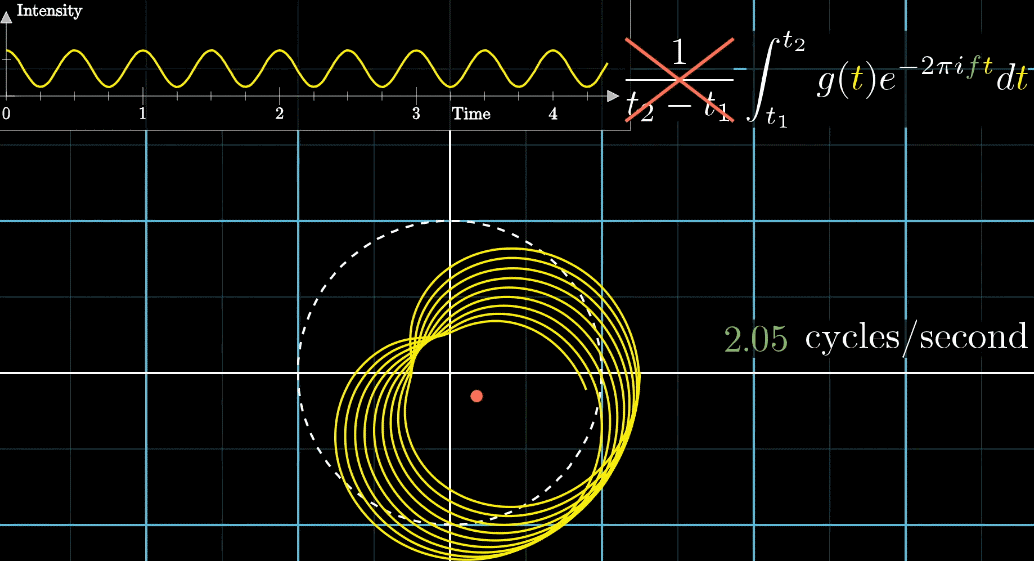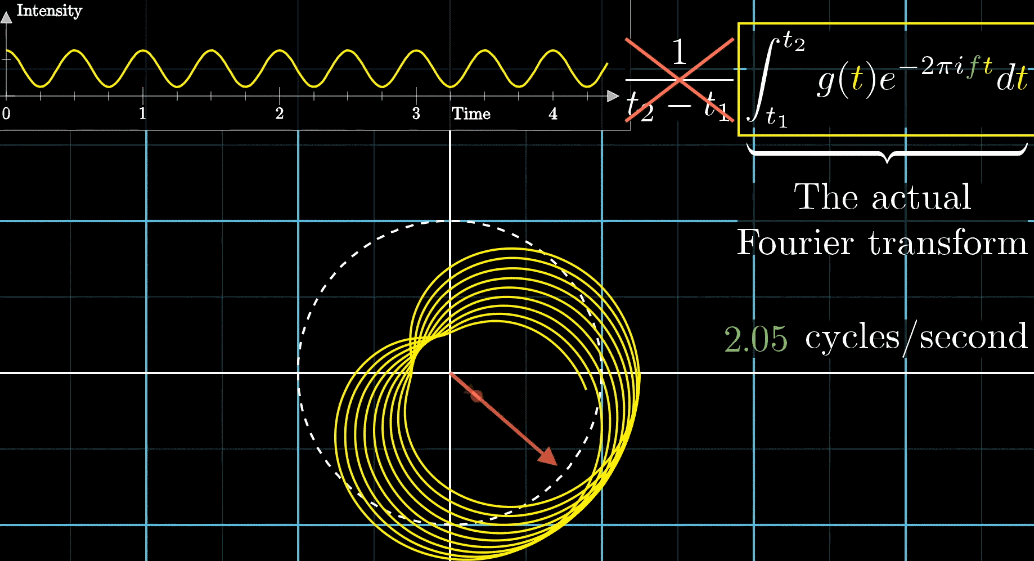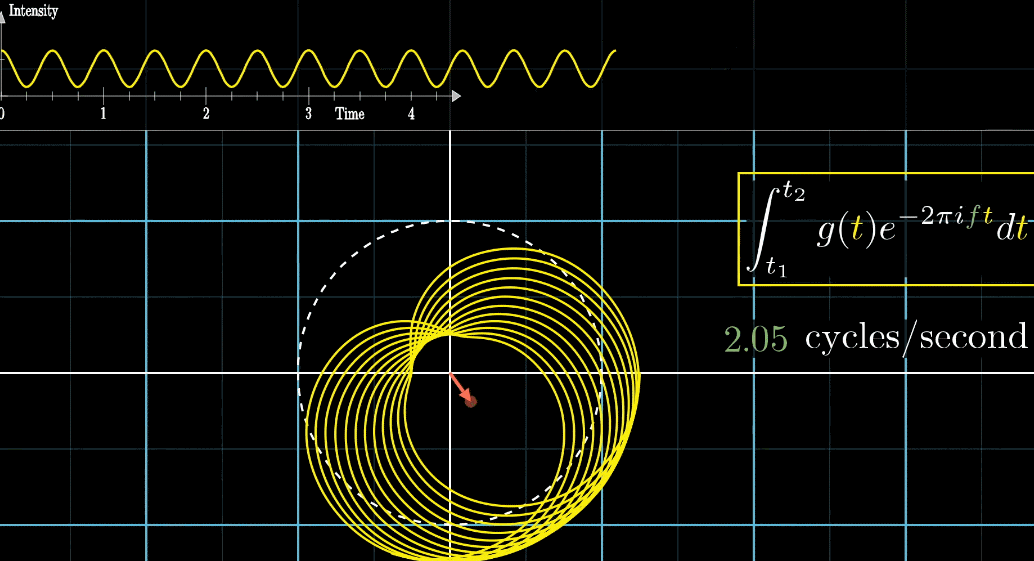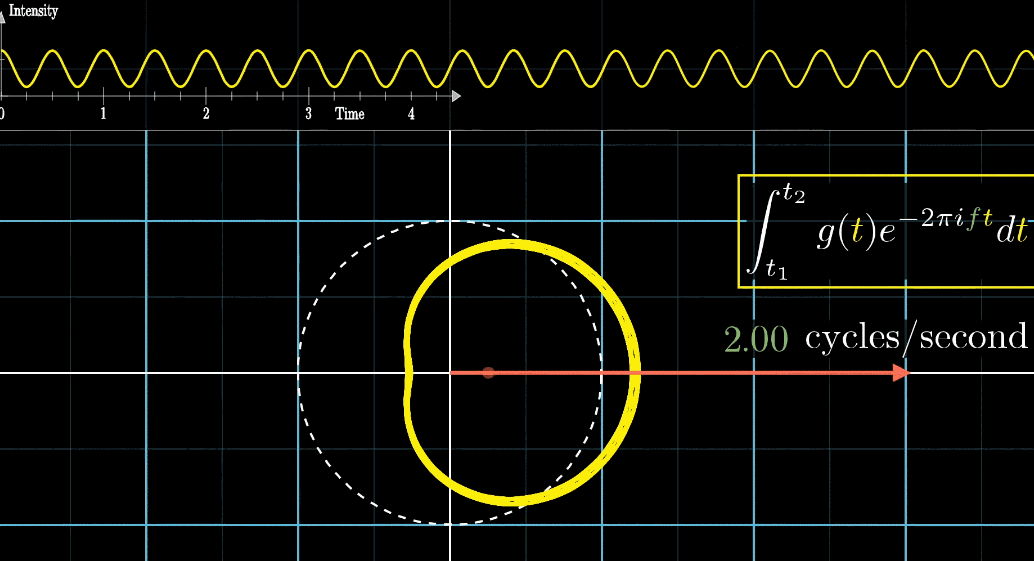
• 圆周围的图像由白色的箭头绘制而成，速度可变，上图中的白色箭头移动速度是每秒钟转过白色虚线半圈（这个速度是对于下面的圆形图像来说，每秒钟在白色虚线圆形图像中转半圈），对应上面的则是虚线表示一圈走到的位置，0.5拍子/秒。

注意看，在上面的坐标轴，白色虚线画在Time=2秒的位置，表示：下面的白色虚线圆形图像中，转完一圈完成需要2秒

• 此时，有两个频率在起作用，一个是信号的频率：3次震荡/秒，另一个是图像缠绕中心圆（白色虚线圆形）的频率，为0.5圈/秒。第二个频率可以自由改变，相当于一个变量，下面的动图直观的展现了缠绕速度变化时（上面的白色虚线）的可视化表现

从最开始的下面的白色虚线圆形0.79圈/秒（注意这里的速度是指绕白色虚线单位圆的【白色箭头】的滑动速度）一直变化到1.55圈/秒，到最后的恰好让缠绕中心圆的频率3圈/秒，和信号的频率3拍/秒相同，此时会出现一个非常稳定的图像，我们可以理解成：同步。这个绕圈图像记录了原信号的幅值变化并且每一圈都相同（周期性）

在这个特殊的情况下，当坐标轴上面的白色实线箭头到达高峰时，下面的白色实线箭头会同步地达到黄色的最右端

而当坐标轴上面的白色实线箭头到达波谷时，下面的白色实线箭头会同步地达到黄色的最左端，如下图所示

其实，我们只是把一个水平的轴缠绕到一个单位圆上，并用另一个速度的记录标尺（白色箭头）来画图。想当于**从另一个角度（维度）**来看我们的信号

---

质心记录法：新维度的特征提取

虽然新图像挺好看的，但是现在感觉并没法从中看出什么。也不尽然，我们直观的发现，当白色箭头记录的速度在某些特定的值时，画出来的图形非常稳定，形态清晰。那如何表现这个特征呢？

从两个角度来思考

（1）自变量是什么？（输入特征）

输入是一个可变化的转圈速度，既然可变，不妨把它看作自变量，即$f(x)$中的$x$

（2）输出（新的圆圈图）有什么特征？（输出特征）

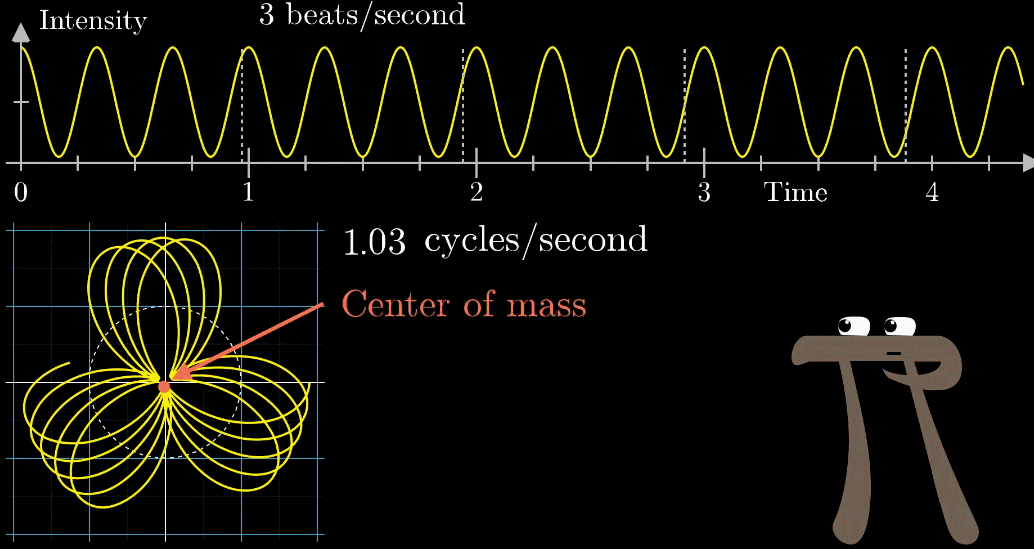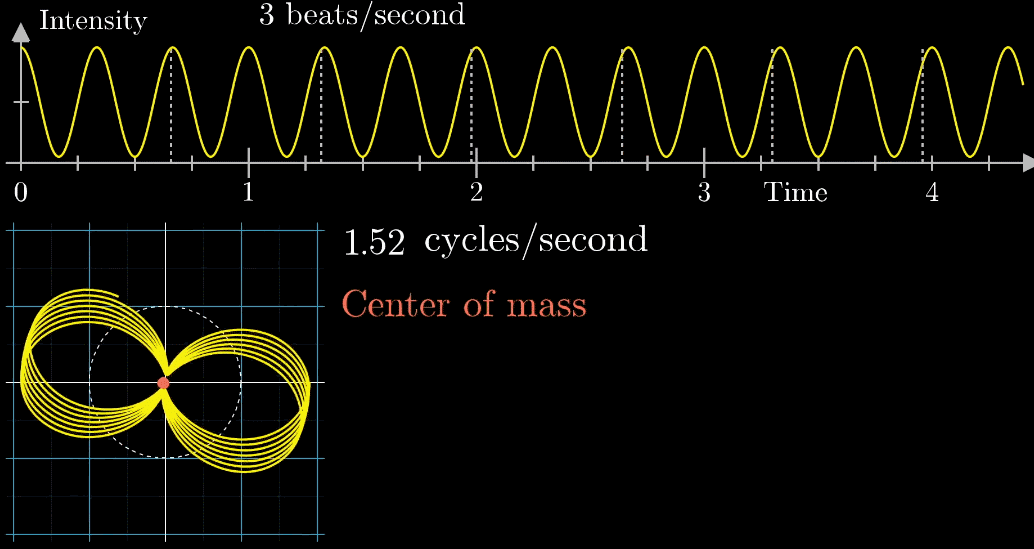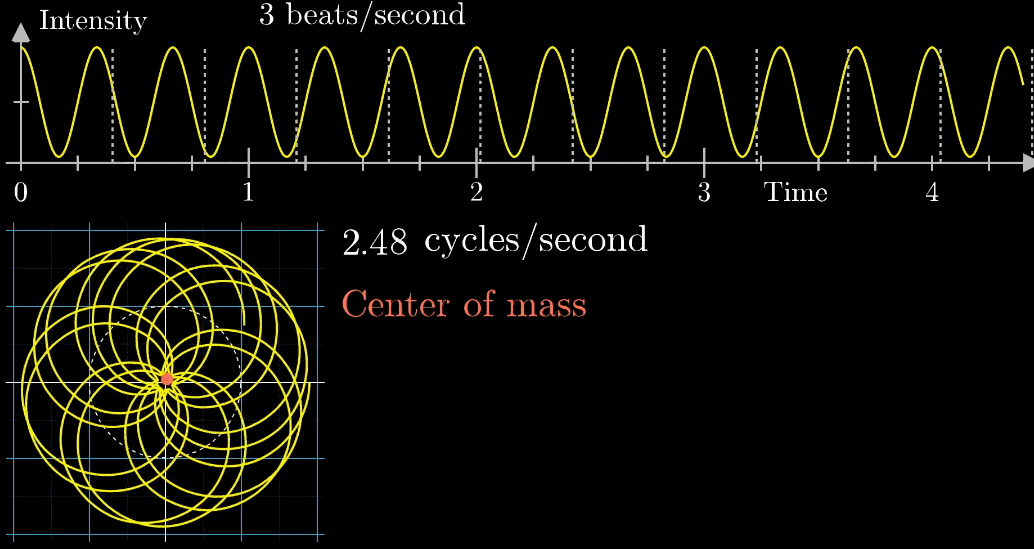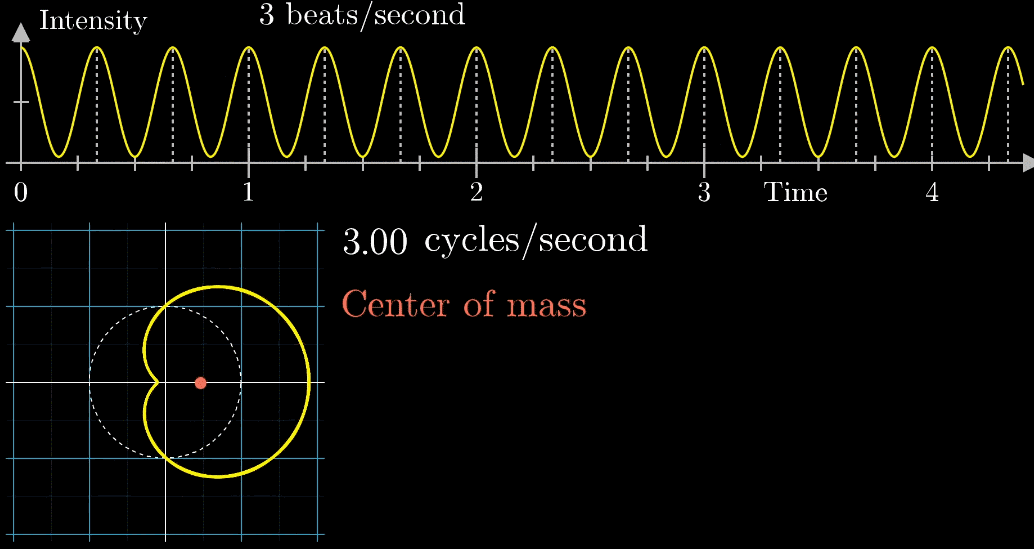
观察到，当**图像很混沌（没有规律，混乱的）**时候，图像基本关于原点对称；稳定时，其实是“头重脚轻”的。描述“头重脚轻”最好的方法当然是用【质心】（它描述了物体的空间分布特征） ，下面的动图直观展现了质心特征对图像特征的描述能力（红色点为质心）

考虑到质心其实是一个二维坐标，这里为了简洁和直观，取质心的横坐标来表示质心的特征

那么新图像的横坐标和纵坐标表示什么如下所示：

【输入（横坐标）】➜【进行采样的（白色箭头）的绕圈速度】

【输出（纵坐标）】➜【圆圈图的质心位置的横坐标】

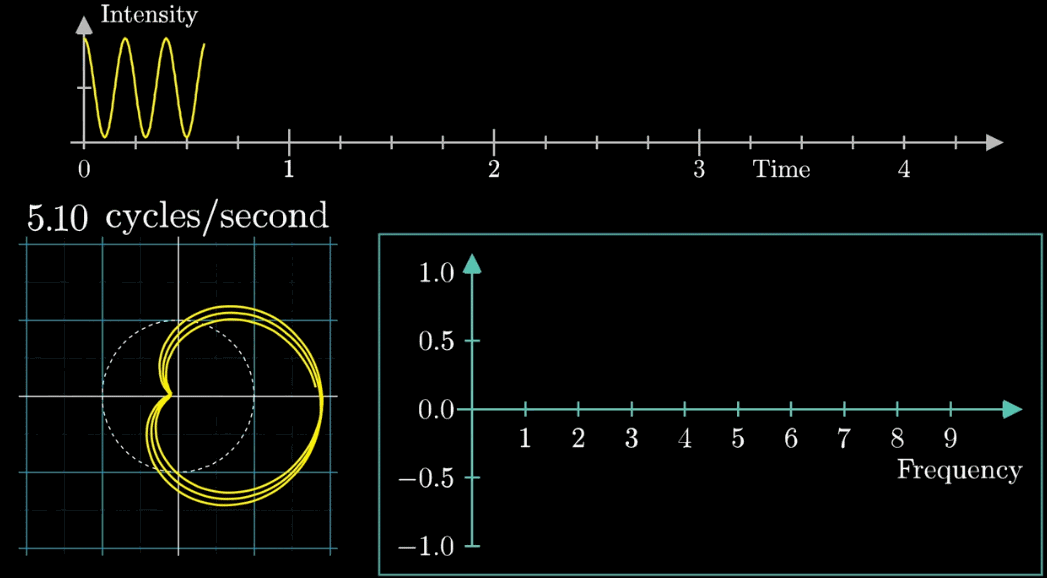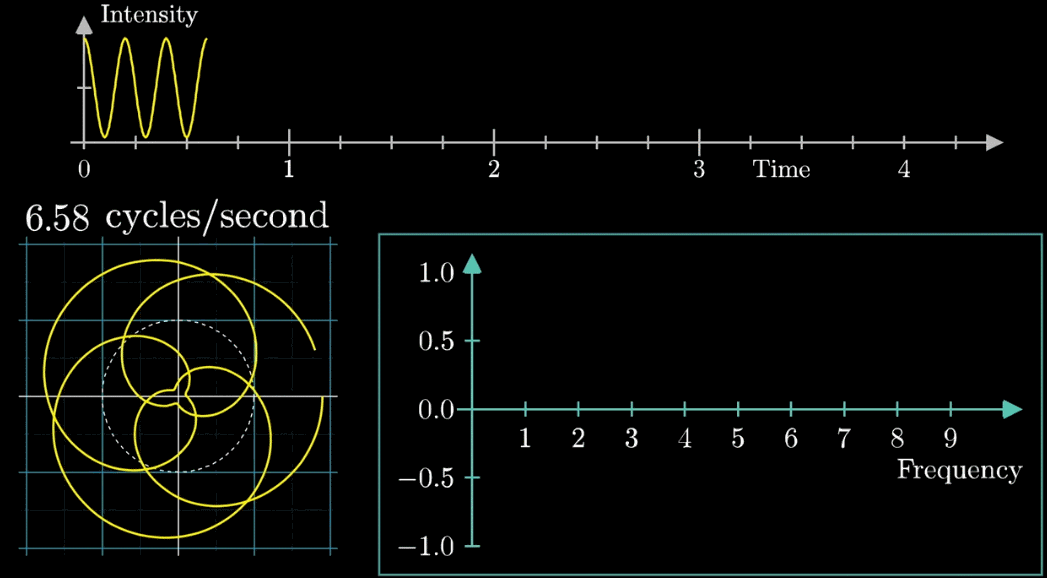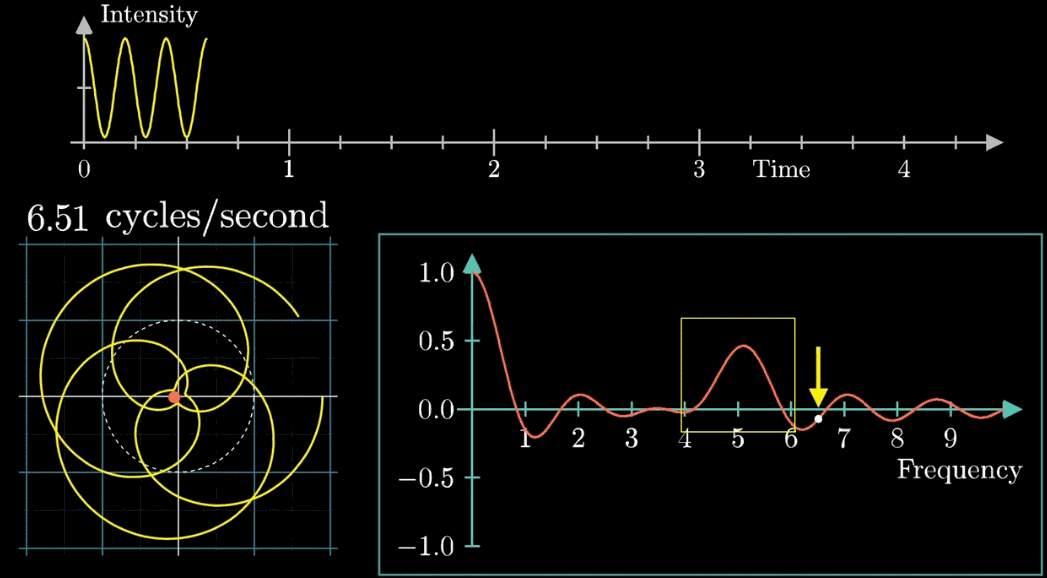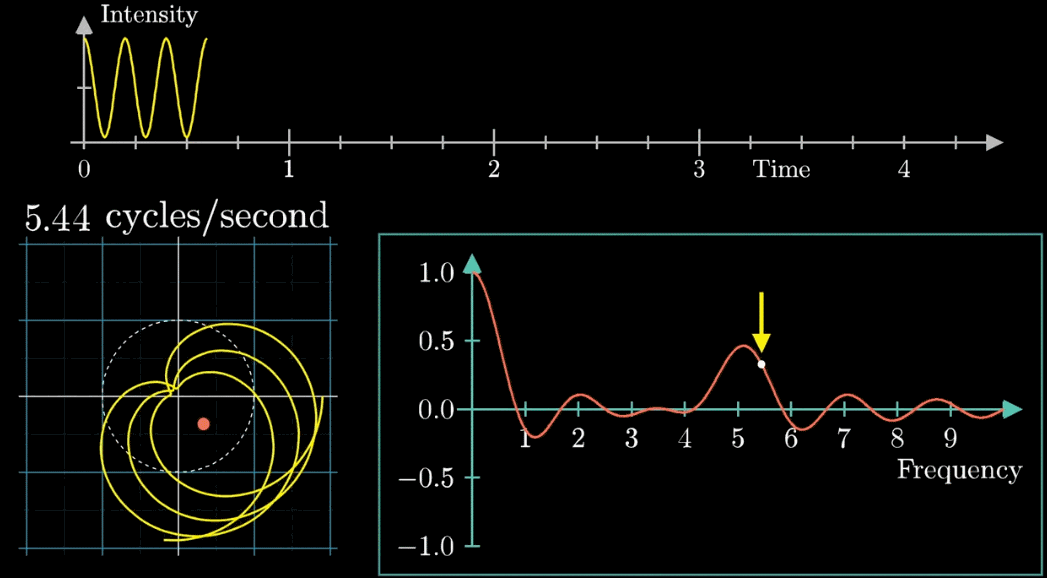
按照上面的说明来记录绘出图像，记录每个缠绕频率（速度）对应的质心位置，参看下列动图，随着图像的绘制到3圈/秒这个位置的时候，是不是感到似曾相识呢？

补充一点，在横坐标等于零点处有一个很大的值，只是因为原来的图像没有关于横轴对称，有一个偏移量，直观参看下面动图，如果把偏移量去除，其实就变成了个$cos(x)$函数

关注点是当频率为3时的凸起，当缠绕频率和信号频率相等时，就出现了一个尖峰，这个图是“近似傅里叶变换”

当缠绕频率和信号频率相等时，“质心”会离坐标轴中心很远，而傅里叶变换的核心就是，如果注意图像质心和频率的变化关系，质心位置能反映出原信号中频率强度，而质心和原点的距离就表示了频率强度，质心与横轴夹角的角度对应着频率的相位

我们可以看到，新图像的横坐标写的是【频率 Frequency】，即缠绕圆圈的记录速度，所以强烈建议看到频率，想起速度，并且抽象为围着圆圈跑的速度（个人感受，对理解【频率】的概念有助益）

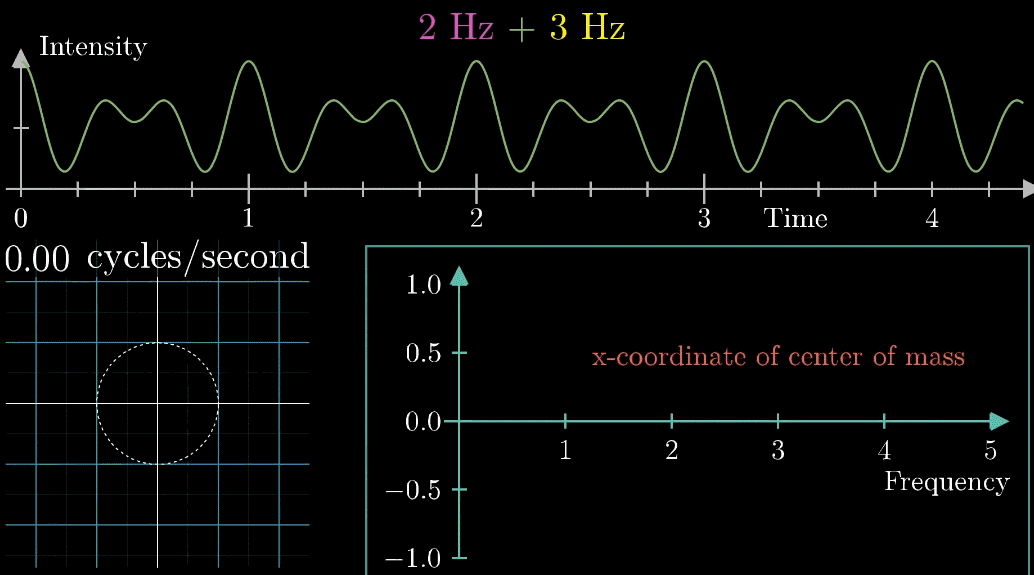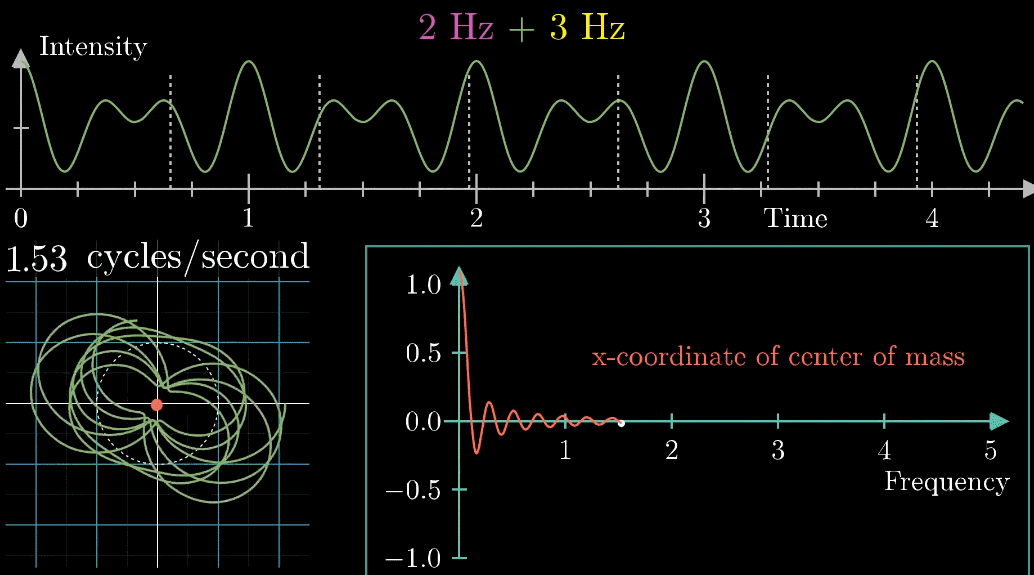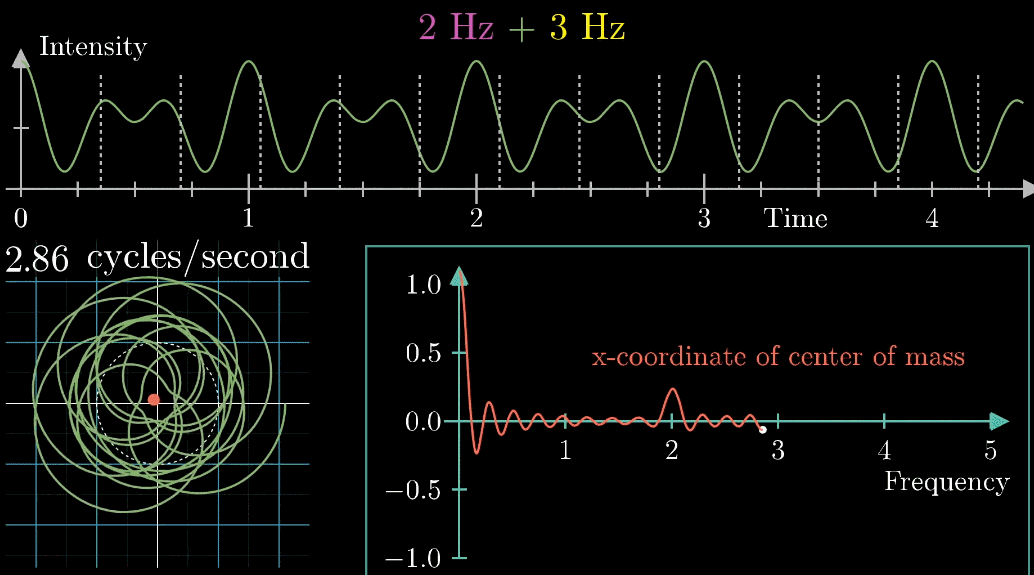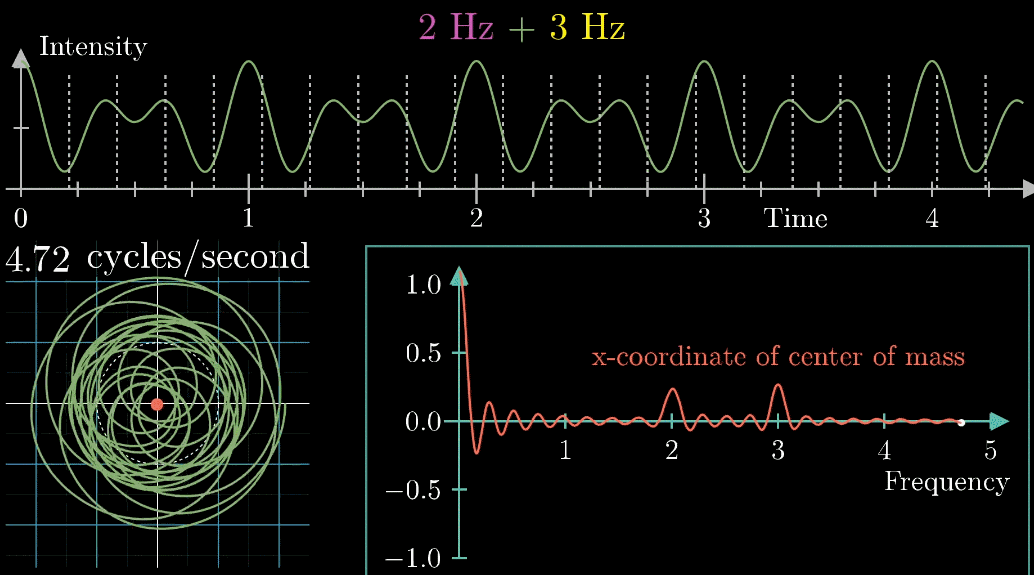
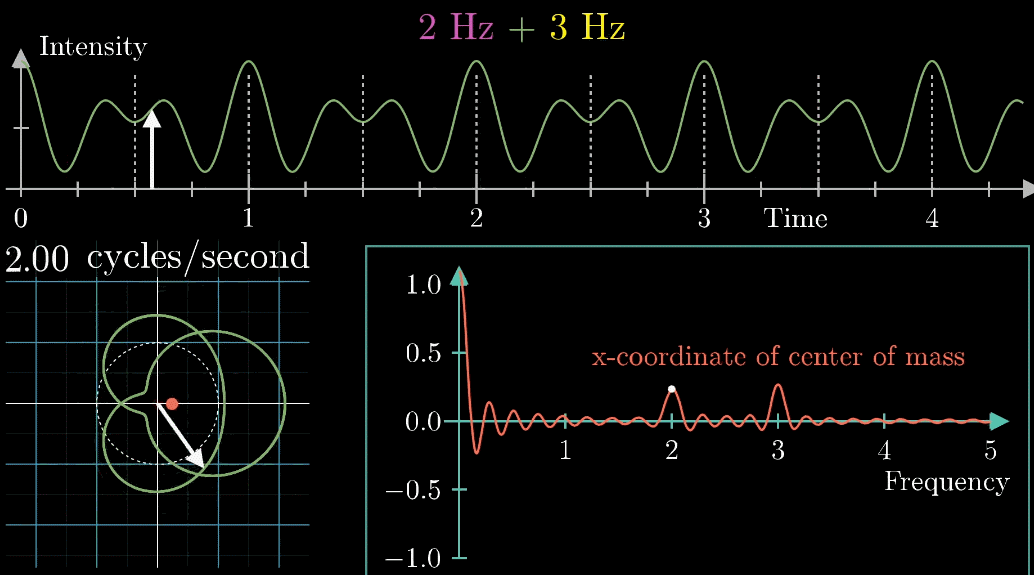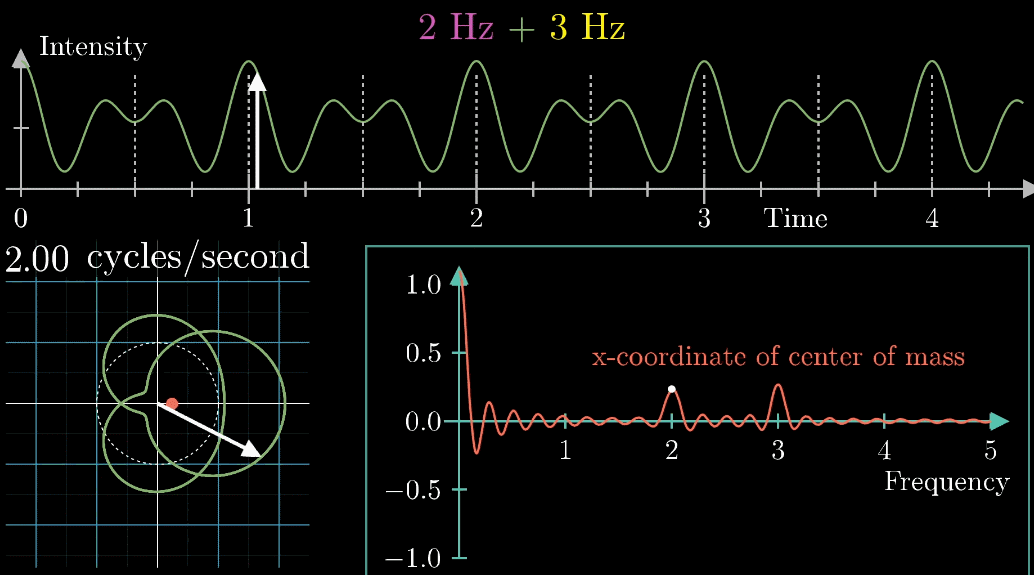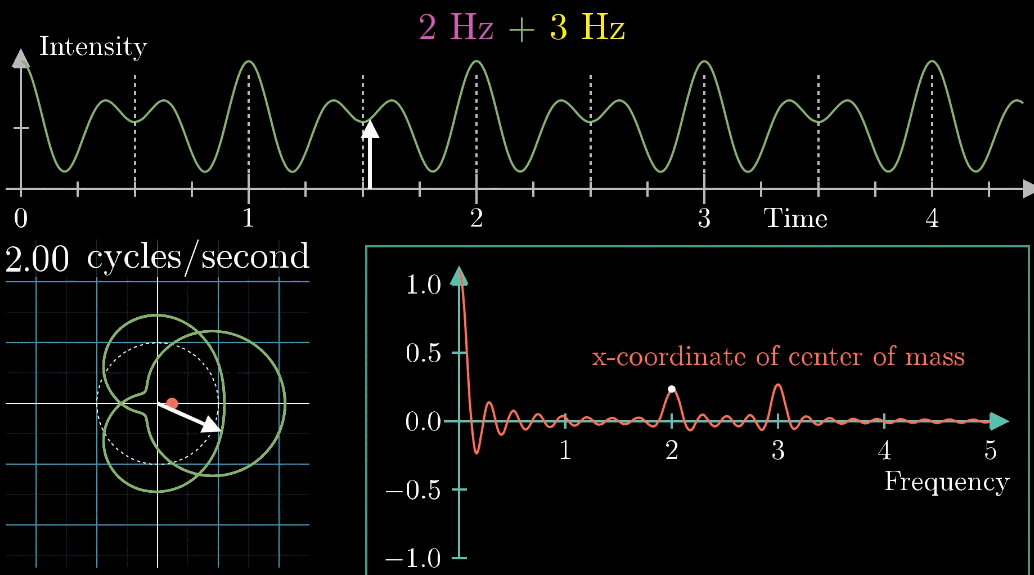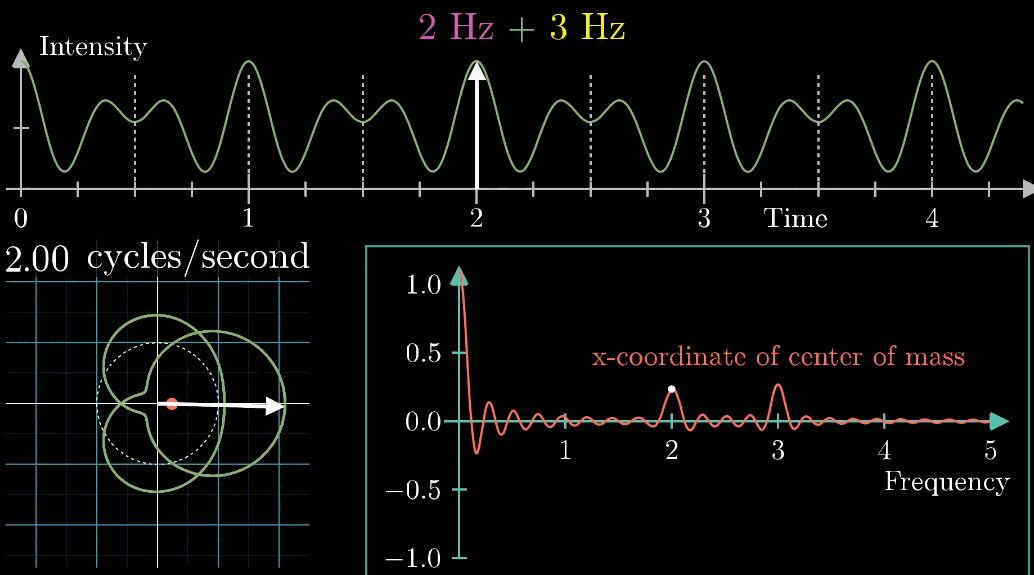
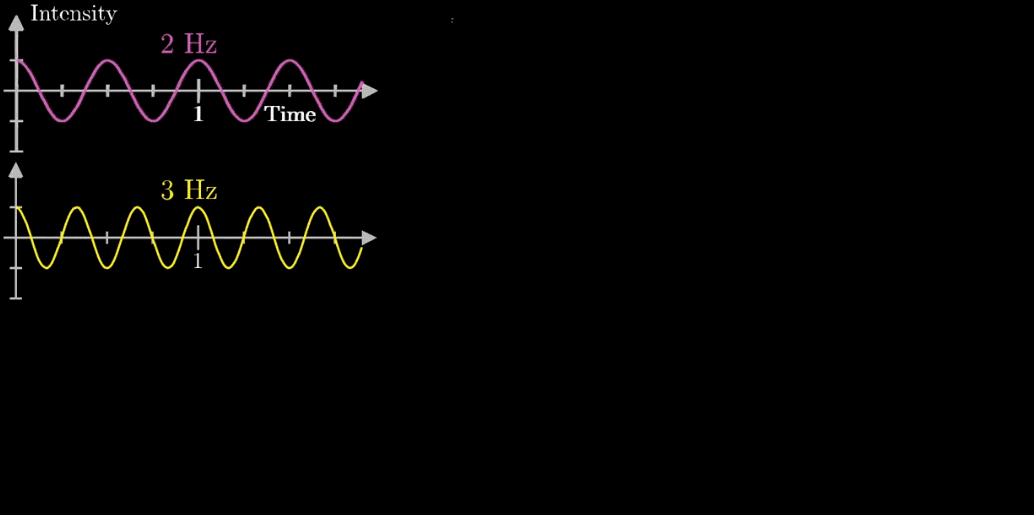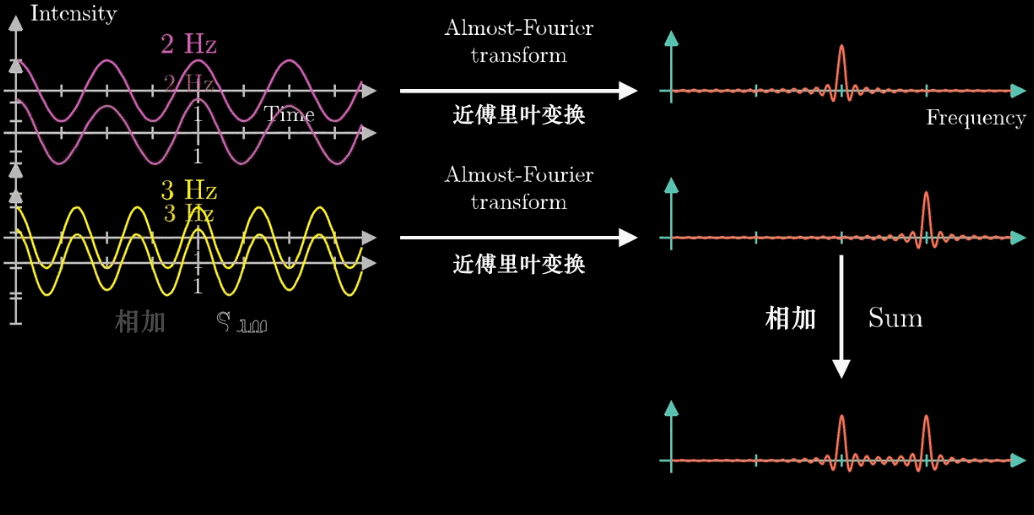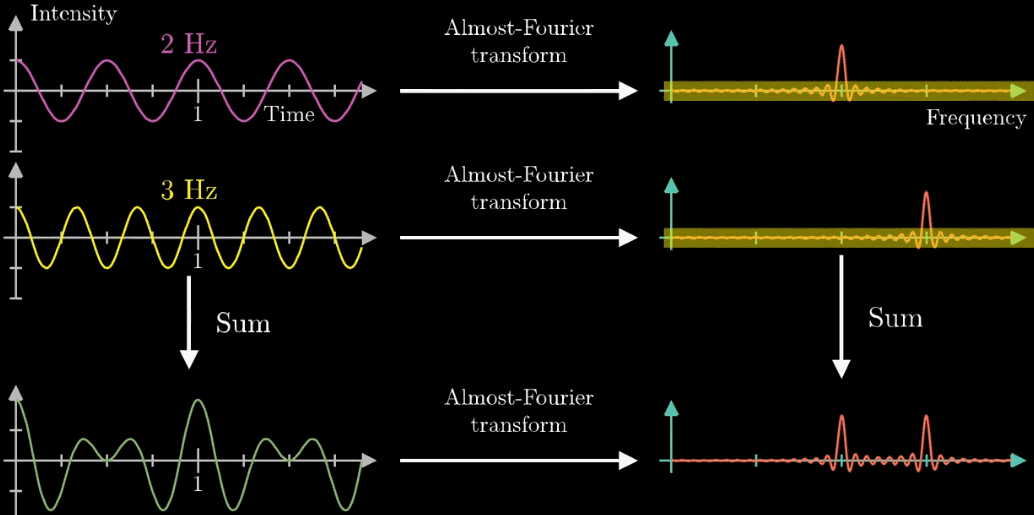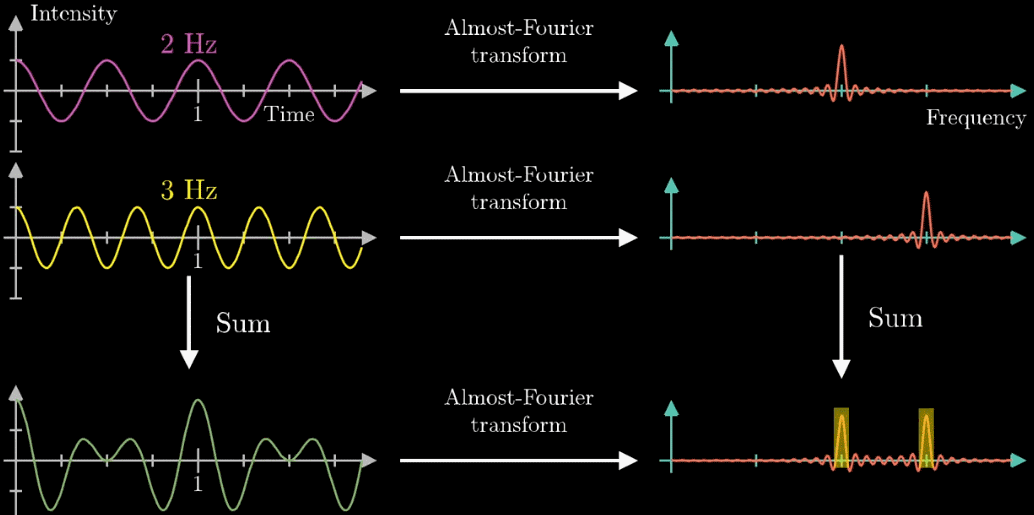
好！有了这个工具，先把它应用到两个声音的组合图像中看看效果：（这是我最喜欢的一张动图）

对于将2Hz和3Hz组成在一起的声音，当缠绕频率和信号频率都等于2转/秒时，右下角的图出现了一个峰值，并且质心处于x轴并离原心最远，而且左下角的图片变得不是那么“混乱”，以上的几个“特征”都说明了当缠绕频率=信号频率=2转/秒时的特殊性

同理，当缠绕频率=信号频率=3转/秒时，也发生了相似的特征

什么？还是没看清上面的振动图像如何变成圆圈图的？看下面的动图，缠绕圆圈速度为2圈/秒的白色箭头将时间信息映射到圆圈图中的的可视化。再次重复，白色箭头以一定的速度（频率，一秒几圈）在上图中向右横移，同时，在下面的单位圆内被转换成类似钟表指针移动的圆圈运动，并记录振幅，画出图像【左下角的图中，白色箭头实际上是沿着“绿色”线逆时针地移动，如果把白色箭头抽像出来，它还是按着白色虚线进行旋转的】

BTW，图形的一部分有点像动画EVA中某个使徒的脸，带给人一种诡异的仪式感。数学之令人敬畏，可能在这一刻熠熠生辉，刺的人睁不开眼

---

公式表示

大家也发现了，我们已经通过这样一个缠绕机器完成了时域到频域的转换，总得来说，参看下面的动图

在下面这个图中，

一种是先将2Hz和3Hz频率转成对应的“近似傅里叶变换”图，再将两个“近似傅里叶变换”图叠加起来

另一种是，先将2Hz和3Hz频率叠加起来，再转成换“近似傅里叶变换”图

这两种在最终得到的“近似傅里叶变换”图都是一样的

这就为我们的“分离”工作带来的最重要的工具，因为我们发现了“可分离”的工具

这是一种【近傅立叶变换】，为什么是【近】，后面会提到。先考虑，那如何数学语言表达这个【转圈记录机制（工具 or 机器）】呢？

第一步：旋转的表示

如下面的动图所示，在这个工具中，非常关键的就是转圈，即表达旋转这种运动，根据第一大部分，这个桥梁，就是复平面，其背后的原理是幂函数结合泰勒公式

著名的欧拉公式说明，在复平面(comples plane)上，$e^{ix}=cos(x)+isin(x)$，当$x=\pi$时，欧拉公式变成$e^{\pi i}=-1$

而咱们这儿，使用公式$e^{ni}$，表示：从单位圆最右边开始，沿着半径为1的单位圆“逆时针”走到n个单位长度的点上，按照这样的理解，$e^{\pi i}=-1$就是在单位圆沿着半径为1的单位圆逆时针走了$\pi$个长度，最终到达了x轴-1的位置

---

更进一步，幂函数中，以$e$为底的函数有着特殊的性质，如下面动图所示，$\pi$单位的 $e^{6.28i}$就表示一个单位圆的360°旋转，则$e^{2\pi it}$表示的就是一秒钟一圈的旋转方程(因为对于单位圆来说，$2\pi$就是一圈的长度），但旋转的速度感觉有点太快了

所以，再加一个$f$频率，从而控制旋转的速度不那么快，图中$f$是$\frac{1}{10}$，合起来表示一秒钟十分之一圈

第二步：缠绕的表示

首先，依据下面的动图所示，在傅立叶变换中，我们规定旋转是顺时针的（规定只是为了统一标准，并且有时候也会考虑书写简洁和方便计算），所以，需要对$e^{2\pi it}$先加一个负号【因为原始$e^{2\pi it}$是逆时针旋转】。假设原来的函数是$g(t)$ ，将两者的幅值相乘就能得到缠绕图像，$g(t)e^{-2\pi ift}$ ，可以说是相当机智了！

从原来的沿着白色虚线滑动，到沿着黄色实线滑动

而这样的转变，只是简单的将$e^{2\pi it}$乘以g(t)，让其依照函数值大小被缩放。这样就能将这个长度不断变化的旋转向量，看作为“缠绕图像”

当然，得到“缠绕图像”还只是中间的一个过程，重点是为了得到“缠绕图像的质心”是怎样变化的

第三步：质心的表示

那如何表示质心这一概念呢？粗略想一下感觉挺难的，但是看起来很难的问题，有一种解决问题的途径是【演绎推理】，先从简单的特例出发，推广到一般，最后证明正确性即可

考虑如何求一个正方形的质心位置，我们只需在边框上取n个等距离分布的点，并且算这几个点的位置的平均值。那么推广到一般情况，也使用类似的采样点的方式解决，如下面动图所示（紫红色的点即采样点），得到

$\frac{1}{N} \sum_{k=1}^{N} g(t_k) e^{-2\pi i f t_k}$

随着采样点的增加，假设增加到无穷个点，需要使用积分来求解这个问题，如下面动图所示，得到

$\frac{1}{t_2-t_1} \int_{t_1}^{t_2} g(t) e^{-2\pi i f t} dt$

这个公式的结果，是缠绕图像的质心

最终步：整理积分限和系数

然而，真.傅里叶公式是没有常数系数$\frac{1}{t_2-t_1}$的，只是$\int_{t_1}^{t_2} g(t) e^{-2\pi i f t} dt$，如果忽略表达倍数关系的系数$\frac{1}{t_2-t_1}$，对应的含义也会发生变化，不再是质心，而是信号存在的时间越久，位置是质心位置乘以一个倍数，它的值就越大。

参看下面的动图，如果原波形持续时长为3秒，那么新的位置就是原来质心位置的3倍；

如果原波形持续时长为6秒，那么新的位置就是原来质心位置的6倍

如果某个频率持续了很长时间，这个频率的傅里叶变换的模长就被放得很大

而去掉常数系数$\frac{1}{t_2-t_1}$的几何直观动图变为（红色箭头为去掉系数后的长度表示），最本质的区别是：可以使得最后绘制的图像更集中在对应的频率的附近，或者说在对应的频率位置的值更大

$\hat g(f)=\int_{t_1}^{t_2} g(t) e^{-2\pi i f t} dt$

对于傅里叶置换求出来的值，我们使用$\hat g(f)$来表示，$\hat g(f)$表示了对应原信号中某一频率的强度

这里的自变量是频率f，因为只有当对频率进行改变，才能找到“凸起”

如下图，$\hat g(2) $和$\hat g(3)$的值明显大于其它频率值

这里的t1是频率开始时刻，t2时频率结束时刻

继续考虑上下限。我们知道，一般傅立叶变换公式的上下限是正负无穷，那它的几何直观是什么呢？参看下面动图，其实就是看看信号持续时间无穷大是什么样子的

说实话，这个动图解答了我大学时代的一个疑惑，音乐文件不都是有时间长度的嘛，我就一直不懂，凭什么对负无穷到正无穷做傅立叶变换？原来真实情况是，从负无穷到0，音乐结尾到正无穷，就像上面的动图，其实都没有振动幅值（电信号幅值）与之对应，再结合缠绕圆圈的思想：原来，从音乐开始到结束做傅立叶变换和从负无穷到正无穷做傅立叶变换，是特么的一回事啊！（吐槽完毕）

$\hat g(f)=\int_{-\infty}^\infty g(t) e^{-2\pi i f t} dt$

$t$是时间

$f$是频率

$2\pi i$是欧拉公式的一部分

---

尾巴

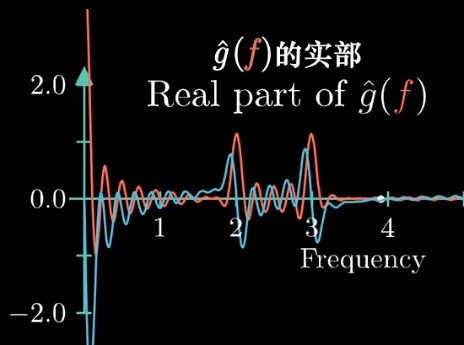
还有一个坑，即在表示质心的时候，我们只取用了x轴坐标，下面的图中的蓝色曲线就是纵坐标（y轴 or 虚部）的可视化,红色曲线是横坐标（x轴 or 实部）

原信号的长度

再追根究底一些，因为之前已经提到过，假设我们的信号有4.5s，并且真实的频率是5拍/秒

那么考虑原信号的长度的变化呢？首先，假设时域中信号的长度很长，那么缠绕圆上的线就会更多，每次接近稳定图像质心的变化速度更快（即频域图像更加密集），能把质心运动刻画得越细致？参看下面动图

如果一个时域信号持续时间很长，哪怕缠绕频率偏离了真实频率（5拍/秒）一点点，整个信号也能绕足够多的圈子，变得很均匀对称。当缠绕频率偏离真实频率一点儿时，使得质心的变化速度很快，对应的图像会有一个很大的落差。

那么对应的，如果时域原信号的长度缩短呢？如下面动图所示，频域图像会更加稀疏。原因同理，当缠绕的内容少的时候，重心变化的速度也相应的变慢了。只有当缠绕频率和真实频率相差很大时，才能显示出**“对称性”**

或者说，观察的时间越短，对具体频率的把握就越差

比如，当两辆车都开着双闪，乍一看，感觉两辆车是“同步”地双闪，但看的时间一长了，两辆车就不那么同步了，因为两辆车有各自的闪频率

但如果观察的时间越长，对具体频率的把握就越好

还是，当两辆车都开着双闪，如果持续观察了几分钟，感觉两辆车是“同步”地双闪，那么就有更大的把握说明，两辆车是“同步”的

这里的观察时间长，就对应时域中信号的长度很长，反之也是

总得来说，基本就上述内容就详细解释了下面的现象：

时域的信号周期越长，那么频域的范围越小，就越集中（越能找到“同步”的频率），越不容易发生混叠，越容易抽象出时间信号的周期性重复信息，此时自然而然的，周期性这个词就出现了。

时域的信号周期越短，就对应傅里叶变换就越广，越广范的频率

只有0.05秒的同一个频率音频，让人判断是音频的范围，那只能把从低音到高音都纳入进去

但如果是10秒的同一个频率音频，就能很准确地判断是什么频率

另外，可以自己思索一下，比如无穷时间的周期时域信号呢？又比如一个恒定振幅（一个电平）的时域信号呢？其实这里就给出了一个提示有关为什么傅立叶变换有那么多需要考虑的变形了，因为在缠绕这件事情发生的过程中，有几种情况是特别的（这部分3B1B视频并没有讲解，可能需要未来再更新了）

傅里叶的引申应用

在雷达探测中，经常使用傅里叶转换，由上面我们知道，短脉冲对应的傅里叶变换一定很广范围，长脉冲对应的傅里叶变换是短范围。

如果雷达向外面发送的是短脉冲，在时域里面，很容易将多个不同速度的物体进行区分开，但在频域里面

如果想得到精确的速度，那就一定需要一个频率范围很窄的回波（对应时域中需要长脉冲），这就是“傅里叶不可兼得”效应，不能同时准确地获得两个变量

总结

讲了这么长，至此全部结束。估计读者都已经晕了，那么，在这里为【看到】傅立叶变换做一个总结，就来总得说说我们从头到尾都干了些啥？参看下面动图

• （1）$e^{2\pi i}$表示单位圆，添加自变量即可表示旋转
• （2）与原函数相乘缠绕到单位圆上
• （3）为求质心的特征，进行积分计算

一步一步写出傅立叶变换公式的联想链条（如何记忆）

• 一个逆时针旋转360°画成的圆 ➜ $e^{2\pi i}$

  • $2\pi i$ 用来表示：从圆最右侧开始，绕着圆逆时针的距离，$e^{2\pi i}$是单位圆上的一个位置点

• 表示运动，需要原函数的自变量：时间 t ➜$e^{2\pi i t}$

  • 随着时间t变化，$e^{2\pi i t}$在单位圆上的不同位置点

• 表示旋转速度，需要自变量，频率 f➜ $e^{2\pi i t f}$

  • $f$单纯用来控制旋转速度

• 规定变换的采样方向为顺时针，加负号 ➜ $e^{-2\pi i t f}$

• 乘以原函数缠绕到单位圆并记录 ➜ $g(t) e^{-2\pi i t f}$（此处使用g符号标识原函数是为了和频率符号区分）

  • $g(t)$相当于用来改变幅度，让上面的绿色箭头，沿着黄色实线进行滑动。【原来是沿着白色虚线滑动】

• 为了计算质心特征，积分 ➜ $\int_{-\infin}^{\infin} g(t) e^{-2\pi i t f}$

• 自变量为频率 ，写出函数表达式 ➜ $\hat g(f)=\int_{-\infin}^{\infin} g(t) e^{-2\pi i t f}$

傅里叶的本质

当缠绕频率和信号频率相等时，“质心”会离坐标轴中心很远，而傅里叶变换的核心就是，如果注意图像质心和频率的变化关系，质心位置能反映出原信号中频率强度

质心和原点的距离就表示了频率强度

质心与横轴夹角的角度对应着频率的相位

质心和原点的距离就表示了频率强度，如图所示

质心与横轴夹角的角度对应着频率的相位

而在峰值（比如是5拍/秒）时有一点分散的原因是，那些接近5拍/秒的纯正弦波，几乎也匹配这个信号

参考

https://www.zhihu.com/question/19714540/answer/325895339

https://www.bilibili.com/video/av19141078/

https://charlesliuyx.github.io/2018/02/18/【直观详解】让你永远忘不了的傅里叶变换解析/

https://www.youtube.com/watch?v=spUNpyF58BY

https://www.youtube.com/watch?v=KuXjwB4LzSA

https://www.youtube.com/watch?v=mkGsMWi_j4Q

https://www.youtube.com/watch?v=g8RkArhtCc4

https://www.youtube.com/watch?v=8rrHTtUzyZA

离散傅里叶变换

真.傅里叶变换$\hat g(f)=\int_{-\infty}^\infty g(t) e^{-2\pi i f t} dt$

由于计算机只能处理有限长的离散信号，因此必须建立对应的离散傅里叶变换DFT（Discrete Fourier Transform）：

$\hat g(f) = \sum_{n=0}^{N-1} g(n) e^{-2\pi i f \frac{n}{N}}$

---

我们令$\zeta=e^{-2\pi i m/N}$，如下图所示，这里的$\zeta$是欧拉方程中的$e^{-2\pi i/N}$，用来表示单位圆上不同的位置点

假设例子中，N=8

$\zeta^0=e^{-2\pi 0/8}$

$\zeta^1=e^{-2\pi 1/8}$

……

$\zeta^7=e^{-2\pi 7/8}$

$\zeta^8=e^{-2\pi 8/8}$ ,$\zeta^8$相当于$\zeta^0$逆时针转了一圈

将$\zeta$乘以不同的数，会得到不同的幅度值

简单来说

$\zeta$是单位圆上的位置点，也可以看作为方向(angle)。

而s[0],s[1]这样的系数，是幅度值(length)

$s[0]\times\zeta$ 就成了指向x轴方向幅度是某个值的向量

图中的$\hat s[0]$表示频率$f=0$，当频率等于零时，会得到一个周期($T=\frac{1}{f}$)无限长的正弦波，也就是一条直线。

现在，我们把在图中取的8个点及对应的幅度值相乘并累加起来，得到

$\hat s[1]=s[0]\times\zeta^0+s[1]\times\zeta^1+s[2]\times\zeta^2+....s[7]\times\zeta^7$

这里的$\hat s[1]$就与之前讲到的**“质心”没有除以$\frac{1}{t_2-t_1}$的式子（即真.傅里叶变换）**有点相似

这里的$\hat s[1]$，1代表的是频率$f=1$，此时，左侧的图长得像个cos函数

当频率$f=2$时，左侧的图还是个cos函数，但明显周期变小，频率变大了

而此时，对应右侧的图也发生了变化

$\hat s[2]=s[0]\times\zeta^0+s[1]\times\zeta^2+s[2]\times\zeta^4+....s[7]\times\zeta^{14}$

因为频率变了，$\zeta$ 的位置也会跟着频率发生变化

如果把$\hat s[1]=s[0]\times\zeta^0+s[1]\times\zeta^1+s[2]\times\zeta^2+....s[7]\times\zeta^7$ 公式做个抽像出来

离散傅里叶转换公式

$\hat s[f]=\sum_{n=0}^{N-1}s[n]\zeta^{f n}=\sum_{n=0}^{N-1}s[n]e^{-2\pi i f n/N}$

$f$为频率

$n/N$为离散的时刻，这里$n\in (1,N)$【$n/N$对应连续的t, $t\in (t_1,t_2)$ 】

$2\pi i$是欧拉公式一部分,$i$是虚数根

$N$是多项式维数

和上面的连续傅里叶变换公式其实很相似，我们的关注点还是在同样的时间段内，通过不断改变频率$f$，找到一个$\hat s[f_{p}]$是极大值，那么这个$f_{p}$就是让**“信号频率”和“缠绕频率”相同的频率**

---

将上面的离散傅里叶转换公式写成代码

import numpy as np

def dft(signal):
    N=len(signal)
    zeta = np.exp(-2*np.pi * i /N)
    #f的范围0,1,2,3……N-1  N-1可以取到
    for f in (0,N):
        #n的范围0到N-1
        sum=0
        for n in (0,N):
            #s代表signal
            sum+=s[n]*zeta^(n*f)

上述代码中，有一处可以用来改进：zeta^(n*f)，我们不必在每次计算sum时都算一次$zeta^(n*f)$，因为在离散的情况下，我们的N取得是有限的（比如上面例子中，N=8），那么，我们可以先求出来所有的$\zeta$位置，使用时直接查表，可以加快速度。

import numpy as np

def dft(signal):
    N=len(signal)
    zeta_powers=[np.exp(-2*np.pi * i * n /N) for n in (0,N)]
    #f的范围0,1,2,3……N-1  N-1可以取到
    for f in (0,N):
        #n的范围0到N-1
        sum=0
        for n in (0,N):
            #s代表signal
            #直接查表
            sum+=s[n]*zeta_powers[(n*f)%N]

虽然已经对上述代码进行了改进，但代码的复杂度还是$\mathcal{O}[N^2]$，对于相同规模，使用DFT和使用FFT的差距还是十分明显的

对于N=90000的数量，使用DFT计算需要40s，而使用FFT计算只要14ms

---

由于计算机只能处理有限长的离散信号，因此必须建立对应的离散傅里叶变换DFT（Discrete Fourier Transform）：

$\mathrm{X_k~=~\sum_{n=0}^{N-1}x_n~\cdot e^{-i2\pi k\frac nN}}$

如果我们定义一个矩阵M

$\mathrm{M_{kn}~=e^{-i2\pi k\frac nN}}$

则很明显DFT的公式只是一个简单的线性变换：

$X=x \times M$

因此简单的使用矩阵乘法就能计算出DFT的结果，我们可以很容易的写出DFT的python代码

import numpy as np

def DFT(x):
    N = len(x)
    k,n = np.meshgrid(np.arange(N),np.arange(N))
    W = np.exp(-1j*2*np.pi*k*n/N)   
    return np.dot(x,W)
#1234567

我们以2048点DFT为例，与numpy中内置的FFT做对比，看看速度相差多少

x=np.random.random(2048)
X=np.fft.fft(x)
X=DFT(x)
#123
compute 2048 points dft using np.fft cost: 0.001677 ms
compute 2048 points dft using DFT cost: 0.321912 ms
#12

可以看到，速度相差了差不多2000倍，对于每个值$X(k)$的计算需要N个复数乘法(4N个乘法和2N个加法)和N-1个复数加法(2N-2个加法),因此DFT的总计算量需要$N^2$个复数乘法和$N^2-N$个复数加法，复杂度是$\mathcal{O}[N^2]$ ，是不利于计算机进行实时信号处理的，因此为了优化DFT的计算量，便有了相关FFT算法，下面介绍快速傅里叶变换算法，对于快速傅里叶逆变换其优化方式非常相似，因此不做介绍

快速傅立叶变换

快速傅立叶变换（FFT）是信号处理和数据分析中最重要的算法之一，很多人只是调用现成的库如FFTW，但为了知其所以然，加深对算法的理解，我们有必要搞懂FFT算法是怎么计算的，这里不讨论傅里叶变换的理论和推导，只讨论实际工程中怎样计算，由于python代码的可读性以及计算的方便性，使用python代码展示FFT计算过程

---

FFT有什么用？

如果有多项式$A(x)=a_0+a_1*x+...+a_d*x^d$,$B(x)=b_0+b_1*x+...+b_d*x^d$，我需要求的是他们的卷积，这时，我要在哪使用FFT，对谁使用fft?

要计算两个多项式A(x)和B(x)的卷积，可以使用FFT（快速傅里叶变换）来加速计算。卷积的一般计算方法涉及两个多项式的乘法和求和，而使用FFT可以将卷积计算的复杂度从$O(n^2)$降低到$O(n*log(n))$。

下面是使用FFT计算多项式卷积的步骤：

1. 将多项式A和B分别表示为系数表示形式的数组$(a_0, a_1, ..., a_d)$和$(b_0, b_1, ..., b_d)$。
2. 对两个系数数组进行零填充，使它们的长度都变为2的幂，以便进行FFT计算。
3. 对系数数组A和B分别使用FFT，将它们转换为点值表示形式。
4. 将点值表示的A和B两个多项式相乘，得到点值表示的卷积结果。
5. 对卷积结果使用逆FFT，将其转换回系数表示形式。
6. 去除结果中的零填充部分，得到最终的卷积多项式。

在这个过程中，FFT主要用于将多项式从系数表示转换为点值表示以及从点值表示转换回系数表示。在步骤3和步骤5中使用FFT。

具体代码可能如下所示（假设已经有FFT和逆FFT的函数）：

import numpy as np

def FFT(P):
    n = len(P)

    if n <= 1:
        return P

    omega = np.exp(-2 * np.pi * 1j / n)
    P_even = FFT(P[::2])
    P_odd = FFT(P[1::2])

    factor = omega ** np.arange(n // 2)
    left = P_even + factor * P_odd
    right = P_even - factor * P_odd

    return np.concatenate((left, right))


def IFFT(P):
    n = len(P)

    if n <= 1:
        return P

    omega = np.exp(2 * np.pi * 1j / n)
    P_even = IFFT(P[::2])
    P_odd = IFFT(P[1::2])

    factor = omega ** np.arange(n // 2)
    left = P_even + factor * P_odd
    right = P_even - factor * P_odd

    return np.real(np.concatenate((left, right)))

def convolution(A, B):
    n = 1
    while n < len(A) + len(B):
        n *= 2
    A_padded = np.pad(A, (0, n - len(A)), 'constant')
    B_padded = np.pad(B, (0, n - len(B)), 'constant')
    
    A_fft = FFT(A_padded)
    B_fft = FFT(B_padded)
    
    C_fft = np.multiply(A_fft, B_fft)
    
    C_coeff = np.real(IFFT(C_fft.conj()))
    
    result = C_coeff[:len(A) + len(B) - 1]
    
    return result

# 例子
A = [1, 2, 3]
B = [4, 5, 6]
result = convolution(A, B)
print(result)  # 输出卷积结果

一幅图像A与一个边缘检测滤波器（如Sobel、Prewitt等）的矩阵B进行卷积，可以使用上面提供的卷积函数。

在这种情况下，A代表图像的像素值（将RGB分成三个通道，分别计算），B代表边缘检测滤波器的核矩阵。

首先，需要将图像A和边缘检测矩阵B表示为二维的NumPy数组。

然后，将它们作为输入传递给卷积函数，将返回卷积结果，其中包含了图像A中的边缘信息。

导入

如果有多项式$A(x)=a_0+a_1*x+...+a_d*x^d$,$B(x)=b_0+b_1*x+...+b_d*x^d$，我需要求的是他们的卷积结果（也就是卷积多项式$P(x)$）。

假设为如$P(x)=p_0+p_1x+p_2x^2+...+p_dx^d$，我们想求出来具体的$p_0,p_1,...p_d$系数值。

一般的做法：我们需要**$(d+1)$个P(x)函数输出值**，对应在$P(x)$图上需要$(d+1)$个点，才能解出来$P(x)$的具体系数值，如果不使用FFT，则是个$\mathcal{O}[ N^2 ]$问题，如下图所示

如果使用FFT，可以参考下图的过程。

先将A(x),B(x)由系数值转成点值【使用FFT实现】，再将两者的点值相乘，最后，将点值转成系数值【使用IFFT实现】

---

对称取点

下面，开始将问题简化，对于“偶函数P(x)”如果我们需要在P(x)上至少取8个点，那么最好的方法是依靠“对称性”取点。

同样，对于“奇函数P(x)”，对使用对称性取点

---

拆分多项式

下面，将问题普遍化，对于一个多项式：$P(x)=3x^5+2x^4+x^3+7x^2+5x+1$，受到刚刚“对称取点”的启发，我们可以将这个多项式拆分成由“奇函数”和“偶函数”的和

这样拆分后，好处时“降维”了，将原来5维多项式降成了两个关于$x^2$的2维多项式的组合，即

$P(x)=2x^4+7x^2+1+x(3x^4+x^2+5)$

这里把$x_{old}^2$看作$x_{new}$，从而$P_e(x^2)=2x^2+7x+1$ 是子多项式；$P_o(x^2)=3x^2+x+5$为子多项式，它们都是关于$x^2$的二维多项式

将后面提取出来一个$x$是为了保持括号内的子多项式$P_o(x^2)$和前面的子多项式$P_e(x^2)$拥有相同维度

---

公式推广

将公式推广更普遍一点儿，如果原维度关于x的n维P(x）

$P(x)=p_0+p_1x+p_2x^2+...+p_dx^d$

那么降维后变成了两个关于$x^2的$$n/2-1$维的多项式的组合

取的自变量也不是$x_1,x_2,x_3,...x_n$的$n$个点，而是使用**“对称取点”**的特点，只取$\pm x_1,\pm x_2,\pm x_3,...,\pm x_{n/2}$这$n$个点

对于所有的$+x$，$P(+x_i)=P_e(x_i^2)+x_iP_o(x_i^2)$

对于所有的-x，$P(-x_i)=P_e(x_i^2)-x_iP_o(x_i^2)$

$P_e(x_i^2)$和$P_o(x_i^2)$都是关于$x^2$的$n/2-1$维度。

又因为$P_o(x_i^2)$和$P_e(x_i^2)$都是关于$x^2$的函数，所以对于$P_o(x_i^2)$和$P_e(x_i^2)$来说，$x_{new}$的范围都是$x_1^2,x_2^2,...,x_{n/2}^2$，各自有($n/2$个点)，两个子函数加起来一共有$n$个点。【注意：这里$x_i^2$只有正数，没有负数与之对应，这也就是下面需要引入复数的原因】

对于两个子多项式$P_e(x^2)$和$P_o(x^2)$在$x_1^2,x_2^2,...,x_n^2$上(各自$n/2$个点，一共$n$个点），又可以再次分解，按这方法递归下去，我们最终得到的$\mathcal{O}[ n \log n ]$ 的复杂度

---

但是，现在从理论上论证了：“傅里叶转换的计算确实是可以简化的”，但新的问题来了

对于$[ \pm x_1, \pm x_2, \pm x_3,.... \pm x_{n/2} ]$是 $+$ 与 $-$ 相对应匹配的，可以使用对称取点

而$[ x_1^2,x_2^2,...,x_{n/2}^2 ]$ 不是 $+$ 与 $-$ 相匹配的，即无法使用对称取点

那么，如何让$[ x_1^2,x_2^2,...,x_{n/2}^2 ]$ 也可以使用对称取点，这是新的问题

为了解决这个问题，我们需要引入复数

---

引入复数

为什么要引入复数？下面举例说明下

比如有个多项式$P(x)=x^3+x^2-x-1$，根据上述的原则，我们需要至少选择4个点，再按照对称选点的原则，假设我们选择了"$x_1, -x_1, x_2 ,-x_2$"这四个点

按上述原则，我们将$P(x)$拆分$P(x)=x^2-1+x(x^2-1)$，$P_e(x^2)=x-1=P_o(x^2)$

那对于$P_e(x^2)$和$P_o(x^2)$来说，他们的自变量范围就是$x_1^2, x_2^2$，而且为了符合“对称取点”的原则，这里的$x_2^2$就必须等于$-x_1^2$，即$x_2^2=-x_1^2$，如图所示

从而，$x_1^4$是$(x_1^2)^2$

现在假设$x_1=1$，那么这个树状图的元素按下面的方式进行变化

这里的$x_2^2=-x_1^2=-1$，那么，$x_2$只能取复数$i$，即$x_2=i$，从而，我们成功地引入到了复数

学名：$4^{th}$ roots of unity【4次单位根】

---

更普遍的，对于一个5次多项式，需要至少6个点，为了方便起见，我们选择8个点（$2^3=8$)

推广到所有维度，对于d维度的多项式，需要选择点数的选择条件：$n \geq (d+1) , n=2^k, k \in Z$

这里涉及了个新概念 【n次单位根】

---

n次单位根

先来看下复数域，对于一个单位圆，设角度$angle=\frac{2\pi}{n}$

设$\omega =e^{\frac{2\pi i}{n}}$用来表示在取到不同angle时，单位圆上对应位置点，其中$i \in (0,1,2,.....n)$，当i=0时，$\omega$是x=1点即（$e^{i\theta}=1$)

解释完成后，我们将原来的多项式$P(x)$也转换对应复数域，即在$[ \omega^0 ,\omega^1 ,\omega^2 ,... ,\omega^{n-1} ]$计算$P(x)$

为什么要用$[ \omega^0 ,\omega^1 ,\omega^2 ,... ,\omega^{n-1} ]$计算$P(x)$？

因为$\omega^{j+n/2} = -\omega^j$，也就是说$\omega^{j+n/2} = -\omega^j$是$\pm$匹配的, $n$ roots of unity

而且，在子多项式$P_e(x^2),P_o(x^2)$中，$\omega^{j+n/2} = -\omega^j$也是$\pm$匹配的, $(n/2)$ roots of unity

---

FFT流程

现在，可以开始梳理FFT的整个流程了

首先，已知多项式$A(x),B(x)$的各系数值(coeff)$[a_0,a_1,...,a_{n-1}]$,$[b_0,b_1,...,b_{n-1}]$。而目标是求出他们的卷积结果多项式$C(x)$的各系数值(coeff) $[c_0,c_1,...,c_{n-1}]$

下图中的$P(x)$泛指任意函数

放在代码中就是def FFT(P)

首先，需要找到递归的baseline，当n=1时，即$P(1)$，这时的$P(1)$也是泛指

而FFT的核心是递归过程，一个是$P_e(x^2)$，另一个是$P_o(x^2)$，他们都只有原$P(x)$一半维度

假设$P_e(x^2)$和$P_o(x^2)$的输出分别是$y_e=[P_e(w^0),P_e(w^2),...,P_e(w^{n-2})]$，另一个是$y_o=[P_o(w^0),P_o(w^2),...,P_o(w^{n-2})]$，

$y_e,y_o$都是点值(value)，比这步开始，就已经将系数值coeff转成了点值value

随后，使用$P_e(x^2)$和$P_o(x^2)$ 将$P(x)$还原回去

注意：这里的$x_j=\omega^j, -\omega^j=\omega^{j+n/2}$，将原公式进行替换

同理，使用下面公式再进行替换

$y_e[j]=P_e(\omega^{2j})$

$y_oe[j]=P_o(\omega^{2j})$

$y_e[j]$和$y_o[j]$是子多项式递归的结果

最终的输出

$y=[P_e(w^0),P_e(w^2),...,P_e(w^{n-1})]$

y也是点值value

FFT代码实现

import numpy as np

def FFT(P):
    # P - [p_0, p_1, ..., p_{n-1}] coeff representation
    n = len(P) # n is a power of 2
    
    # Base case
    if n == 1:
        return P
    # Construct omega
    # Note the use of '1j' for the imaginary(i^2=-1) unit in Python
    omega = np.exp(2 * np.pi * 1j / n)
    
    # Split even and odd indices
    # P[0::2] = P[0], P[2], P[4], ...,P[n-2]
    P_e = P[0::2]
    # P[1::2] = P[1], P[3], P[5], ...,P[n-1]
    P_o = P[1::2]
    
    # Recurse
    y_e = FFT(P_e)
    y_o = FFT(P_o)

    # Combine
    y = [0] *n
    # n//2 cuz y_e and y_o are half the size of y
    for k in range(n // 2):
        # y[k] is P(x)=P_e(x^2)+x*P_o(x^2)
        y[k] = y_e[k] + omega**k * y_o[k]
        # y[k + n // 2] is P(-x)=P_e(x^2)-x*P_o(x^2)
        y[k + n // 2] = y_e[k] - omega**k * y_o[k]
    
    return y

---

逆FFT

根据上面离散FFT的过程，想要求系数矩阵$[p_0,p_1,...,p_{n-1}]$，只要对**$\omega$矩阵求逆矩阵**【$\omega$矩阵也是已知的，可以轻松算出来】即可（因为点值矩阵$[P(\omega^0),P(\omega^1),...,P(\omega^{n-1})]$是已经由FFT函数算出来的结果

总结来看，FFT是把系数矩阵(coeff)转成点值矩阵(value)；逆FFT是把点值矩阵(value)转成系数矩阵(coeff)

逆FFT代码

只修改了一行代码

import numpy as np

def IFFT(P):
    # P - [p_0, p_1, ..., p_{n-1}] coeff representation
    n = len(P) # n is a power of 2
    
    # Base case
    if n == 1:
        return P
    # Construct omega
    # Note the use of '1j' for the imaginary(i^2=-1) unit in Python
    # The only line that changed!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
    # The only line that changed!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
    # The only line that changed!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
    omega = (1/n)*np.exp(2 * np.pi * 1j / n)
    
    # Split even and odd indices
    # P[0::2] = P[0], P[2], P[4], ...,P[n-2]
    P_e = P[0::2]
    # P[1::2] = P[1], P[3], P[5], ...,P[n-1]
    P_o = P[1::2]
    
    # Recurse
    y_e = FFT(P_e)
    y_o = FFT(P_o)

    # Combine
    y = [0] *n
    # n//2 cuz y_e and y_o are half the size of y
    for k in range(n // 2):
        # y[k] is P(x)=P_e(x^2)+x*P_o(x^2)
        y[k] = y_e[k] + omega**k * y_o[k]
        # y[k + n // 2] is P(-x)=P_e(x^2)-x*P_o(x^2)
        y[k + n // 2] = y_e[k] - omega**k * y_o[k]
    
    return y

参考

https://www.youtube.com/watch?v=h7apO7q16V0&t=467s

---

Cooley-Tukey快速傅里叶算法是常见的FFT算法，其思想是利用了DFT变换中的对称性和周期性来简化计算

首先我们定义

$\mathrm{W_N}=\mathrm{e}^{-\mathrm{i}\frac{2\pi}N}$

$W_N$满足下面的定义

周期性:$W_N^{k+N} = W_N^kWNk+N=WNk$

对称性:$W_N^{k+\frac {N}{2}} = -W_N^k$

若m是N的约数：$W_N^{mkn}=W_{\frac{n}{m}}^{kn}$

我们只需几行代码就可验证上述特性

def Wn(k,N):
        return np.exp(-1j*2*np.pi*k/N)
12

定义如下一些变量：

N = 8
k = 3
m = 2
n = 2
1234

验证周期性：

print(np.allclose(Wn(k,N),-Wn(k+N,,N)))
1

验证对称性：

print(np.allclose(Wn(k,N),-Wn(k+N//2,,N)))
1

验证可约性：

print(np.allclose(Wn(m*k*n,N),Wn(k*n,N//m)))
1

结果：

True
True
True

基2FFT

根据上面的对称性，我们可以将DFT计算分为两个较小的部分

$\begin{aligned} \mathrm{X_k~=~\sum_{n=0}^{N-1}x_n~\cdot W_{N}^{kn}} \\ &\mathrm{~=~\sum_{m=0}~x_{2m}~\cdot W_{N}^{2mk}~+\sum_{m=0}^{N/2-1}~x_{2m+1}~\cdot W_{N}^{(2m+1)k}} \\ &\mathrm{=\sum_{m=0}^{N/2-1}x_{2m}\cdot W_{\frac N2}^{km}+W_{N}^{k}\sum_{m=0}^{N/2-1}x_{2m+1}\cdot W_{\frac N2}^{km}} \\ &=\mathrm{F}_1\left(\mathrm{k}\right)+\mathrm{W}_\mathrm{N}^\mathrm{k}\mathrm{~F}_2\left(\mathrm{k}\right) \end{aligned}$

这样一个N点变换就分解为了两个N/2点变换，这里F 1 ( k ) F_1(k)F1(k)和F 2 ( k ) F_2(k)F2(k)分别是序列x中的奇数号和偶数号序列的N / 2 N/2N/2点DFT变换，根据以上公式我们也能很快写出python代码：

def R2FFT(x):
   N = len(x)
   N2 = N // 2
   k,n = np.meshgrid(np.arange(N2),np.arange(N2))
   W = np.exp(-1j*2*np.pi*k*n/N2)
   G = np.exp(-2j * np.pi * np.arange(N2) / N)
   X_even = np.dot(x[::2],W)
   X_odd = G*np.dot(x[1::2],W)
   return np.concatenate([X_even+X_odd,X_even-X_odd])
123456789

同样计算2048点DFT，速度如下：

compute 2048 points dft using R2FFT cost: 0.081140 ms
1

对于N = 2 r N=2^rN=2r,很显然两个N/2点的DFT变换还可以继续分解下去，分解为4个N/4的更短的序列，N/4的序列还可以将序列继续分解下去，直到分解为N/2个2点的DFT变换，2点的DFT变换只需要复数加法和减法就能实现，复数乘法计算量减小至( N / 2 ) l o g N (N/2)logN(N/2)logN,复数加法计算量减小至N l o g N NlogNNlogN，算法复杂度为O [ N l o g N ] \mathcal{O}[NlogN]O[NlogN]，大大减少了DFT的计算量，这就是Cooley-Tukey快速傅里叶变换的基本原理，我们将一个DFT变换分解为两个较小的DFT变换，即基2FFT，我们可以通过递归来实现该算法：

def RecursiveR2FFT(x):
    N = x.shape[0]
    if N <= 2:
        return [x[0]+x[1],x[0]-x[1]]
    else:
        X_even = RecursiveR2FFT(x[::2])
        X_odd = RecursiveR2FFT(x[1::2])
        factor = np.exp(-2j * np.pi * np.arange(N//2) / N)
        return np.concatenate([X_even + factor * X_odd,
                               X_even - factor * X_odd])
12345678910

计算2048点DFT速度如下：

compute 2048 points dft using RecursiveR2FFT cost: 0.081140 ms
1

相比前面的版本速度并没有提升,是因为python的递归版本并不高效,并且没有进行并行化的计算,因此,通过观察基2fft的规律我们可以将递归调用的向量乘法转换为并行计算的矩阵乘法以删除递归调用以及并行计算，python代码如下：

def NonRecursiveR2FFT(x):
    L = len(x)
    N_base = 2
    base = L//N_base
    X = np.reshape(x,(-1,base))
    X = np.vstack([X[0]+X[1],X[0]-X[1]]).T
    for n in range(int(np.log2(base))):
        N = X.shape[1]
        W = np.exp(-1j * np.pi * np.arange(N) / N)
        X_even = X[:X.shape[0]//2]
        X_odd = W*X[X.shape[0]//2:]
        X = np.concatenate([X_even+X_odd,X_even-X_odd],axis=-1)
    return X.ravel()
12345678910111213

计算2048点DFT速度如下：

compute 2048 points dft using NonRecursiveR2FFT cost: 0.000327 ms
1

可以看到,速度又提高了一个数量级，相比numpy的fft只差了1倍

基4FFT

当DFT点数N为4的幂时，我们当然可以使用基2FFT算法进行计算，但对于这种情况使用基4FFT算法更为高效，基4FFT的原理与基2FFT类似，只不过是将N点DFT序列拆分成4个N/4的子序列：

$\begin{aligned}\mathrm{X_k=\sum_{n=0}^{N-1}x_n\cdot W_N^{kn}} \\ = W_N^0F_0\left(k\right)+W_N^kF_1\left(k\right)+W_N^{2k}F_2\left(k\right)+W_N^{3k}F_3\left(k\right) \end{aligned}$

在这里直接给出非递归的基4FFT代码：

def NonRecursiveR4FFT(x):
    L = len(x)
    N_base = 2
    base = L//N_base
    X = np.reshape(x,(-1,base))
    X = np.vstack([X[0]+X[1],X[0]-X[1]]).T
    butterfly_matrix = np.array([[1,1,1,1],[1,-1j,-1,1j],[1,-1,1,-1],[1,1j,-1,-1j]])
    for n in range(int(np.log(base)/np.log(4))):
        N4 = X.shape[1]
        N = N4*4
        G = np.exp(-2j * np.pi * (np.arange(N4).reshape(1,-1)*np.arange(4).reshape(-1,1)) / N)
        X = G*X.reshape((4,-1,N4)).transpose([1,0,2])
        X = np.dot(butterfly_matrix,X).transpose([1,0,2]).reshape((-1,N))
    return X.ravel()
1234567891011121314

注意，由于N = 2048 = 2 ⋅ 4 5 N=2048=2\cdot 4^5N=2048=2⋅45,因此我们最后分成了1024个2点FFT，如果N NN是4的幂例如N=1024,那么最后会得到2个512点的结果，并不满足基4FFT的条件，那么我们可以将这2个512点序列按照基2FFT原理进行计算，最终得到1024个FFT点的计算结果，这实际上是一个混合了基2FFt和基4FFT的混合基FFT算法。