LeetCodeCamps—Day1

day1的三个题目都可以使用快慢指针/双指针/多指针的思路，

慢指针用于存放结果，快指针是遍历原数组用的

27. 移除元素

https://leetcode.cn/problems/remove-element/

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

  • 更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
  • 返回 k。

示例 1：

1
2
3
4
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

1
2
3
4
5
输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

提示：

  • 0 <= nums.length <= 100
  • 0 <= nums[i] <= 50
  • 0 <= val <= 100

思路

理解问题

  • 需要原地“移除”等于val的元素，但又不关心留下的前k个元素之后的内容（暗示不用真的移除）

核心步骤

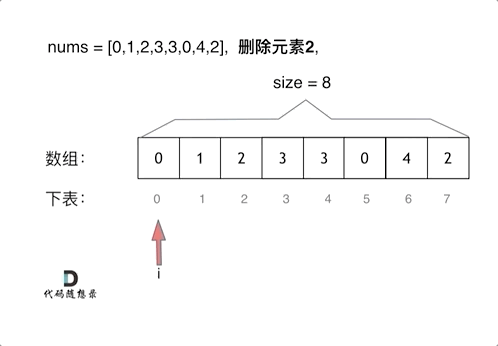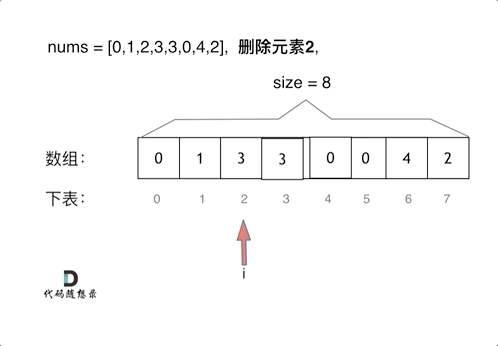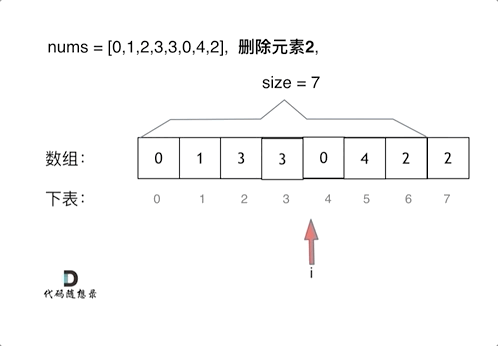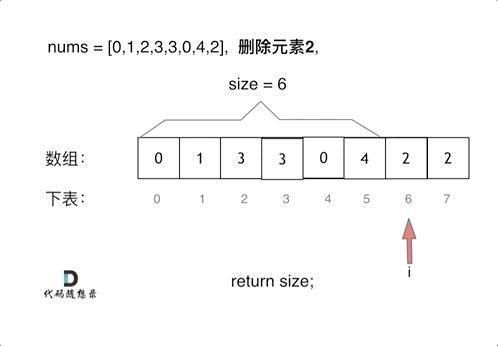
  1. 派用两个指针，快指针用来遍历nums每个数据，判断是否等于val
  2. 慢指针是res结果数组的下标，用来存放不等于val的数据
  3. 本题可以不使用额外空间，直接原地将nums当成res数组

动画参考

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def removeElement(self, nums: List[int], val: int) -> int:
      	# resIndex 为慢指针
        resIndex = 0
        # 先求出L，可以节省每次循环计算len(nums)的时间
        L = len(nums)
        # i其实是快指针，用来遍历每个nums值
        for i in range(L):
            if nums[i] != val:
                nums[resIndex] = nums[i]
                resIndex += 1

        return resIndex

704. 二分查找

题目描述

https://leetcode.cn/problems/binary-search/

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果 target 存在返回下标，否则返回 -1。

你必须编写一个具有 O(log n) 时间复杂度的算法。

示例 1:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

1
2
3
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

  1. 你可以假设 nums 中的所有元素是不重复的。
  2. n 将在 [1, 10000]之间。
  3. nums 的每个元素都将在 [-9999, 9999]之间

思路

理解问题

  1. 有一个升序排序的数组和一个目标值。
  2. 找到目标值在数组中的下标，如果不存在就返回-1。
  3. 算法必须是O(log n)的时间复杂度，这意味着每次操作都要将搜索范围减半（这就是二分查找的精髓）。

核心步骤

初始化指针：用两个指针定义搜索范围：left 指向数组的起始位置（通常是0）。⁠right 指向数组的结束位置（通常是数组长度-1）。

循环查找：

  • 计算中间位置：mid = left + (right - left) / 2; // 这样计算避免整数溢出。

比较数组中mid位置的元素：

  • 如果 nums[mid] == target，返回 mid（找到了！）
  • 如果 nums[mid] < target，说明目标在右半部分，所以更新 left = mid + 1。
  • 如果 nums[mid] > target，说明目标在左半部分，所以更新 right = mid - 1

重复这个过程，直到 left > right（搜索范围为空）

结束处理：如果循环结束还没有找到目标，返回 -1

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        L = len(nums)
        leftIndex = 0
        rightIndex = L - 1
        # 注意跳出条件是小于或等于；如果仅有小于，则会出现nums=[5]输出结果为-1的错误情况
        while leftIndex <= rightIndex:
            # 找到个中值pivot, 不断让num[pivot]与target进行判断
            pivot = (rightIndex + leftIndex) // 2
            # 如果nums[pivot]大于target，则target在[left,pivot]区间
            if nums[pivot] > target:
                rightIndex = pivot - 1
            elif nums[pivot] < target:
                leftIndex = pivot + 1
            else:
                return pivot
        
        return -1

思路二

二分查找的变体：查找数组中第一个大于等于target的元素下标，同样可以适用于这题

核心思想

  1. 同样通过left, right两个指针，不断 shrink 区间；
  2. 但对于nums[mid] == target的情况需要特殊处理，不能直接返回，因为需要找“第一个大于等于target的”，需要带着mid继续搜索

举例

例如，假设数组是 ⁠[1, 5, 5, 7, 9] 和 ⁠target = 5：

mid 是 2 (nums[2] = 5 >= 5)，设置 right = 2，

下次迭代会继续检查左侧[1，5，5]

mid 是 1 (nums[1] = 5 >= 5), 设置 right = 5,

下次迭代会继续检查左侧[1，5]

mid 是 0 (nums[0] = 1 < 5), 设置 left = mid + 1 = 1，此时left == right， 跳出循环

代码二

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        L = len(nums)
        left = 0
        right = L - 1
        # 跳出条件是当left == right
        while left != right:
            mid = (left + right) // 2
            if nums[mid] >= target:
                right = mid
            else:
                left = mid + 1
        # While left equals to right satisfiy the break condition,
        # nums[left] might not equals to target.
        if nums[right] == target:
            return left
        return -1

977. 有序数组的平方

https://leetcode.cn/problems/squares-of-a-sorted-array/

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 1：

1
2
3
4
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：

1
2
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 已按 非递减顺序 排序

进阶：

  • 请你设计时间复杂度为 O(n) 的算法解决本问题

思路

理解问题

  • nums已经有序
  • 每个数字平方后的结果数组也要有非递减序

核心步骤

数组平方后的最大值，一定出自nums的两端，[-4,-1,0,3]->[0,1,9,16]

所以可以在两端使用两个“快指针”，

  1. 比较两端数字平方后的结果，将更大的数字放在“慢指针”的位置
  2. 需要用个res数组，慢指针指向这个res数组
  3. 需要从后向前遍历慢指针，因为题目要求结果数组非递减序

可以参考这个动画（偷来的）

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def sortedSquares(self, nums: List[int]) -> List[int]:
        L = len(nums)
        res = [0] * L
        # resIndex作为结果数组的下标（当成慢指针也行）
        resIndex = L - 1
        # leftIndex和rightIndex当成快指针
        leftIndex = 0
        rightIndex = L - 1
        while resIndex >= 0:
            leftNumSquare = nums[leftIndex]*nums[leftIndex]
            rightNumSquare = nums[rightIndex]*nums[rightIndex]
            if leftNumSquare < rightNumSquare:
                res[resIndex] = rightNumSquare
                rightIndex -= 1
            else:
                res[resIndex] = leftNumSquare
                leftIndex += 1
            resIndex -= 1
        return res