LeetCodeCampsDay9字符串part02
LeetCodeCampsDay9字符串part02
字符串反转/kmp算法/重复字符串的查找
151. 反转字符串中的单词
https://leetcode.cn/problems/reverse-words-in-a-string/
给你一个字符串 s ,请你反转字符串中 单词 的顺序。
单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。
返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。
**注意:**输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中,单词间应当仅用单个空格分隔,且不包含任何额外的空格。
示例 1:
1 | 输入:s = "the sky is blue" |
示例 2:
1 | 输入:s = " hello world " |
示例 3:
1 | 输入:s = "a good example" |
提示:
1 <= s.length <= 104s包含英文大小写字母、数字和空格' 's中 至少存在一个 单词
**进阶:**如果字符串在你使用的编程语言中是一种可变数据类型,请尝试使用 O(1) 额外空间复杂度的 原地 解法
思路
- 先去年多余的空格,可以使用快慢指针思路,当快指针遇到字符时,先给slow添加个空格,当作每两个单词之间的空格(当然slow不能为0);再同时推进slow与fast,将fast指向的单词转移到slow的位置
- 再将整体反转
- 最后,将每个单词反转for i in range(L + 1): if i == L or s[i] == " ": 这里需要注意跳出的条件,因为有时最后一个词也需要反转,但最后一个词后面是没有空格的,所以需要将i的范围从0到L都遍历一遍,并且遇到i==L时,再做一次反转(特殊情况)
代码
- 时间复杂度O(N)
- 空间复杂度O(1)
1 | class Solution: |
右旋字符串(第八期模拟笔试)
题目描述
字符串的右旋转操作是把字符串尾部的若干个字符转移到字符串的前面。给定一个字符串 s 和一个正整数 k,请编写一个函数,将字符串中的后面 k 个字符移到字符串的前面,实现字符串的右旋转操作。
例如,对于输入字符串 “abcdefg” 和整数 2,函数应该将其转换为 “fgabcde”。
输入描述
输入共包含两行,第一行为一个正整数 k,代表右旋转的位数。第二行为字符串 s,代表需要旋转的字符串。
输出描述
输出共一行,为进行了右旋转操作后的字符串。
输入示例
1 | 2 |
输出示例
1 | fgabcde |
提示信息
数据范围:
1 <= k < 10000,
1 <= s.length < 10000;
思路
- 将整体反转
- 再将前k个反转,以及剩下的L-k个反转
代码
1 | class solution(): |
KMP算法
核心是求“子串的最长相等前后缀”
比如"aabaaf",对f来说,它的子串(即aabaa)的最长相等前后缀是"aa"
前缀不包含最后一个尾字母,后缀不包含首字母
kmp学了忘,忘记再学,哎,之前都没理解深刻,这次发现了一个很有意思的两个重点
- left指针是个重点,它是“已经匹配上的前缀的长度”,而且它不是单调变化的
- kmp每次将前n个字符与后n个字符进行匹配,并且n逐个减一地再进行循环匹配,完美解决了“最长前后缀”的匹配问题
KMP思路
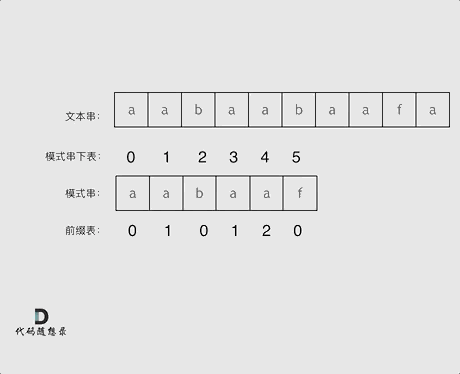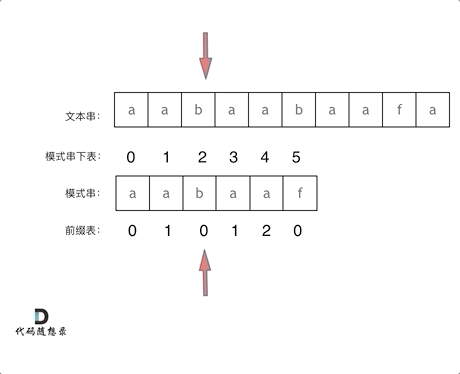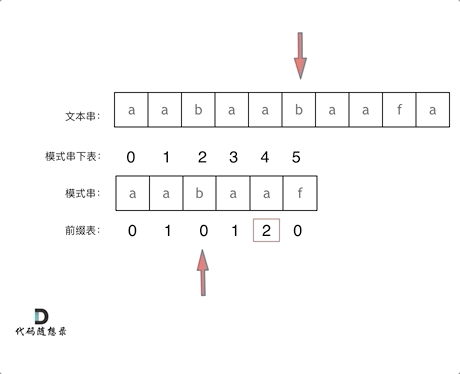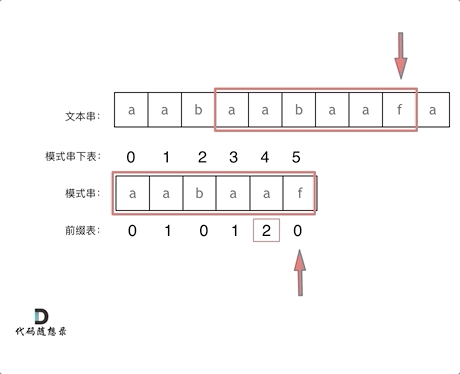
- KMP的核心思路是找“子串的最长相等前后缀”(所谓的前缀表,即,prefix或next数组)
- 比如aabaa的最长相等前后缀是"aa",aabaaf的最长相等前后缀是"",aabaafa的最长相等前后缀是"a"
- 可以使用双指针思路来找"最长相等前后缀"
- 将数组一分为二,比如aa|baaf,其中aa为前缀子串;baaf为后缀子串
- left指针:指向已匹配上的前缀的长度,left是非单向的,它初始化为0->1->0->1->2->1,只有当s[left]==s[right]时才递增;否则就会下降
- right指针:指向后缀最后一个位置, right是单向递增的,它只会从1->2->3…->n
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 串 | a | a | b | a | a | b | f |
| 前缀表(next数组) | 0 | 1 | 0 | 1 | 2 | 3 | 0 |
举例求"aabaa"的next数组
初始化left=0;next数组全为0;right=1
| 下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 串 | a | a | b | a | a |
| 前缀表(next数组) | 0 | 0 | 0 | 0 | 0 |
| 变量位置 | left | right |
s[left]==s[right],说明找到了一对最长前后缀"aa"
left更新:left=left+1即下标1(此时需要指向right的位置),left维护的是0~1这个子串里最长前缀的下标
并更新next数组,next[right]=left,更新了下标1位置的next数组,说明长度为1的前缀与**‘a’(1)匹配**
| 下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 串 | a | a | b | a | a |
| 前缀表(next数组) | 0 | 1 | 0 | 0 | 0 |
| 变量位置 | left | right |
While…
- s[left]!=s[right](s[1]!=s[2]),说明’aa’是无法与’b’匹配的
- Left更新left = next[left-1],即left=0
- 然后s[left]再与s[right]判断,此时s[left]!=s[right],再想更新left = next[left-1],但此时left已经为0,无法更新,因为越界了,所以需要添加个判断条件left>0时才能更新left(这一步是在一个while执行的)
If…
- s[left]!=s[right](s[0]!=s[2]),说明’a’无法与’b’匹配
next[right] = left;更新了下标2位置的next数组,说明长度为0的前缀与**'b’匹配**
最后,right更新,指向下标3
| 下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 串 | a | a | b | a | a |
| 前缀表(next数组) | 0 | 1 | 0 | 0 | 0 |
| 变量位置 | left | right |
While…
- s[left]==s[right](s[0]==s[3]),说明’a’(0)是与’a’(3)匹配的,退出while
If…
- s[left]==s[right](s[0]==s[3]),说明’a’(0)是与’a’(3)匹配的
- left += 1, # left = 1
next[right] = left;更新了下标3位置的next数组,说明长度为1的前缀与**‘a’(3)匹配**
最后,right更新,指向下标4
| 下标 | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 串 | a | a | b | a | a |
| 前缀表(next数组) | 0 | 1 | 0 | 1 | 0 |
| 变量位置 | left | right |
While…
- s[left]==s[right](s[1]==s[4]),说明’aa’(0,1)是与’aa’(3,4)匹配的,退出while
If…
- s[left]==s[right](s[1]==s[4]),说明’aa’(0,1)是与’aa’(3,4)匹配的
- left += 1, # left = 2
next[right] = left;更新了下标4位置的next数组,说明长度为2的前缀与**‘aa’(3,4)匹配**
最后,right更新,指向下标5
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 串 | a | a | b | a | a | f |
| 前缀表(next数组) | 0 | 1 | 0 | 1 | 2 | 0 |
| 变量位置 | left | right |
While…
注意,这里虽然只比较了s[left]!=s[right](s[2]!=s[5]),但它实际比较的是**‘aab’(0,1,2)是与’aaf’(3,4,5)不匹配的**,因为**‘aa’(0,1)是与’aa’(3,4)匹配是已知的信息**,只有将s[2]与s[5]判断,就能直接知道这s(0~2)与s(3~5)是否一样了
- s[left]!=s[right](s[2]!=s[5]),说明’aab’(0,1,2)是与’aaf’(3,4,5)不匹配的,于是退而求其次
- left = next[left - 1] # left = 1
- s[left]==s[right](s[1]==s[5]),说明’aa’(0,1)是与’af’(4,5)不匹配的,于是退而求其次
- left = next[left - 1] # left = 0
- s[left]==s[right](s[0]==s[5]),说明’a’(0)是与’f’(5)不匹配的,没得退了,此时left=0
If…
- s[left]!=s[right](s[0]==s[5]),说明’a’(0)是与’f’(5)不匹配的,if不操作
next[right] = left;更新了下标4位置的next数组,说明长度为0的前缀与**‘f’(5)匹配**
最后,right更新,指向下标6
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 串 | a | a | b | a | a | f | a |
| 前缀表(next数组) | 0 | 1 | 0 | 1 | 2 | 0 | 0 |
| 变量位置 | left | right |
KMP一个很神奇的一点是,它每次将前n个字符与后n个字符进行匹配,并且n逐个减一地再进行循环匹配,比如
’aab’(0,1,2)是与’aaf’(3,4,5)不匹配的
然后会比较
’aa’(0,1)是与’af’(4,5)不匹配的,
然后再比较
’a’(0)是与’f’(5)不匹配的
很完美地完成了“最长前后缀”问题
怎么理解left指针是已匹配上的前缀的长度呢
left代表当前子串 s[0...right] 的“最长相等前后缀”的长度。
left同时也是指向“最长前缀”的下一个字符的下标。
- 当
left为 0 时,我们比较s[0]和s[right]。 - 当
left为 1 时,意味着前缀s[0]已经匹配上了,我们接下来要比较s[1]和s[right]。 - 当
left为k时,意味着前缀s[0...k-1]已经匹配上了,我们接下来要比较s[k]和s[right]。
KMP代码
- 时间复杂度O(N)
- 空间复杂度O(N)
1 | def getNext(self, s: str) -> list: |
28. 找出字符串中第一个匹配项的下标
https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/
给你两个字符串 haystack 和 needle ,请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标(下标从 0 开始)。如果 needle 不是 haystack 的一部分,则返回 -1 。
示例 1:
1 | 输入:haystack = "sadbutsad", needle = "sad" |
示例 2:
1 | 输入:haystack = "leetcode", needle = "leeto" |
提示:
1 <= haystack.length, needle.length <= 104haystack和needle仅由小写英文字符组成
思路
- 先求next数组;
- 再进行匹配,不过求next数组的代码和匹配字符串时的代码是相似的,但需要注意
- root串使用「right」指针进行遍历,下标从0开始,而不是求next中的从1开始,一直遍历到len(root)
- 终止条件是当len(subRoot) == left时,说明找到了匹配的下标,此时right - len(subRoot) + 1即是匹配的下标
代码
- 时间复杂度O(N+M), 其中N为haystack长度,M是needle长度
- 空间复杂度O(M)
1 | class Solution: |
459. 重复的子字符串
https://leetcode.cn/problems/repeated-substring-pattern/
示例 1:
1 | 输入: s = "abab" |
示例 2:
1 | 输入: s = "aba" |
示例 3:
1 | 输入: s = "abcabcabcabc" |
提示:
1 <= s.length <= 104s由小写英文字母组成
思路
思路分析看
https://programmercarl.com/0459.重复的子字符串.html#思路
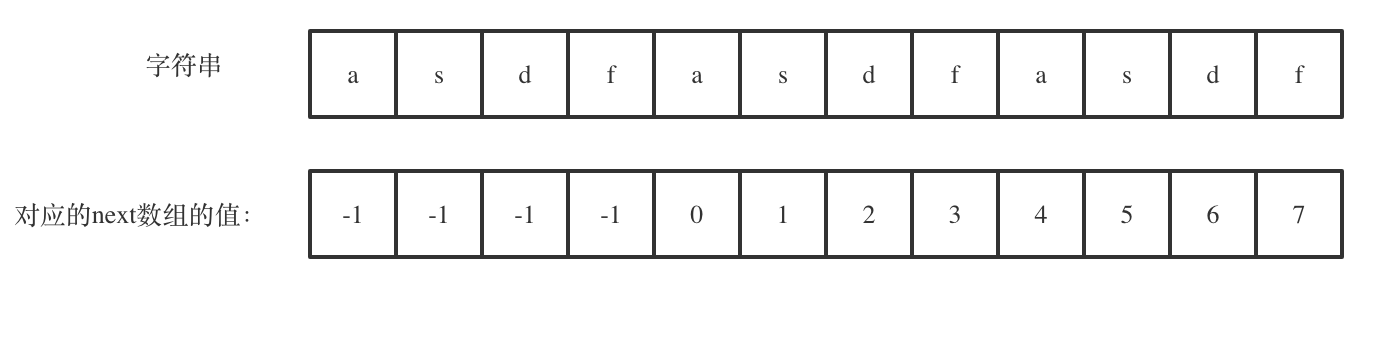
next[len - 1] = 7,next[len - 1] + 1 = 8,8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。
(len - (next[len - 1] + 1)) 也就是: 12(字符串的长度) - 8(最长公共前后缀的长度) = 4, 为最长相同前后缀不包含的子串长度
4可以被 12(字符串的长度) 整除,所以说明有重复的子字符串(asdf)
这种重复的子字符串检测可以应用在“程序中的”密码检测,如果是弱密码比如abcacb,可以进行实时的提醒
代码
- 时间复杂度(N)
- 空间复杂度(N)
1 | class Solution: |