150. 逆波兰表达式求值

https://leetcode.cn/problems/evaluate-reverse-polish-notation/

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

  • 有效的算符为 '+'、'-'、'*' 和 '/' 。
  • 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
  • 两个整数之间的除法总是 向零截断 。
  • 表达式中不含除零运算。
  • 输入是一个根据逆波兰表示法表示的算术表达式。
  • 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

1
2
3
输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

1
2
3
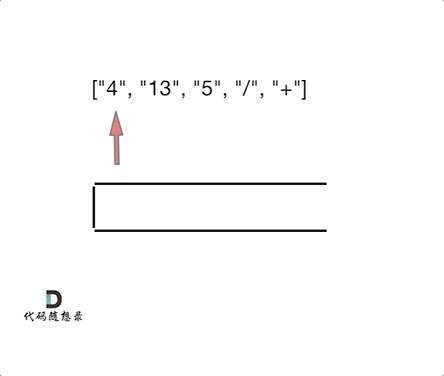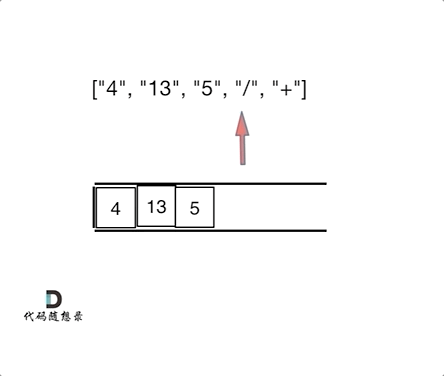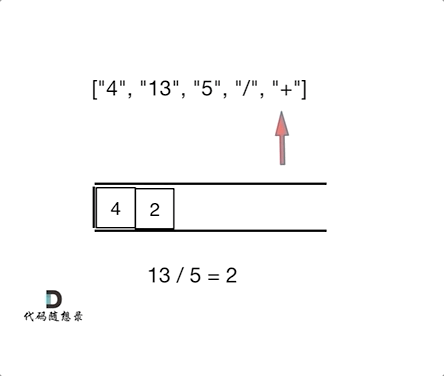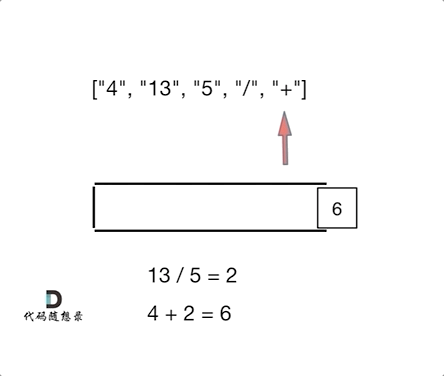
输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

1
2
3
4
5
6
7
8
9
10
输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：
  ((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

提示：

  • 1 <= tokens.length <= 104
  • tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

逆波兰表达式：

逆波兰表达式是一种后缀表达式，所谓后缀就是指算符写在后面。

  • 平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。
  • 该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中

思路

其实逆波兰表达式相当于是二叉树中的后序遍历

  1. 使用个栈实现，遇到数字就进栈，遇到符号则弹出两个数字进行计算，将计算结果再入栈
  2. 本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和1047.删除字符串中的所有相邻重复项 (opens new window)中的对对碰游戏是不是就非常像了

img

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    def evalRPN(self, tokens: List[str]) -> int:
        # 使用个栈实现，遇到数字就进栈，遇到符号则弹出两个数字进行计算，将计算结果再入栈
        # python可用list实现
        curStack = list()
        symbolList = ['+', "-", "*", "/"]
        for i in tokens:
            if i not in symbolList:
                curStack.append(i)
            else:
                if len(curStack) >= 2:
                    num2 = int(curStack.pop())
                    num1 = int(curStack.pop())
                    if i == "+":
                        res = num1 + num2
                    elif i == "-":
                        res = num1 - num2
                    elif i == "*":
                        res = num1 * num2
                    elif i == "/":
                        res = num1 / num2
                    else:
                        return None
                    curStack.append(res)
                else:
                    return None
        
        return int(curStack.pop())

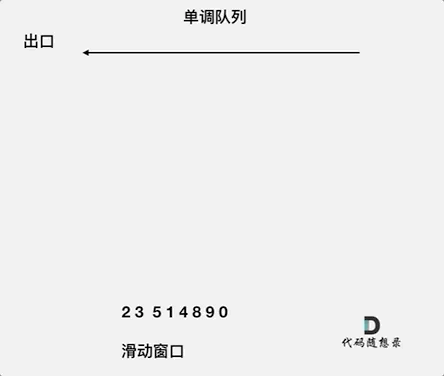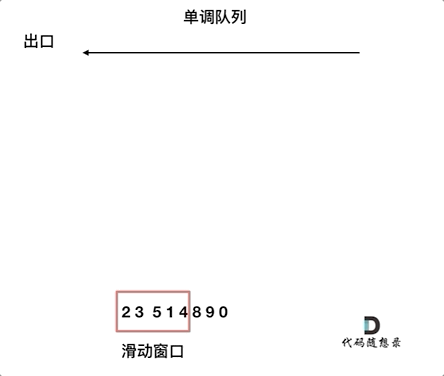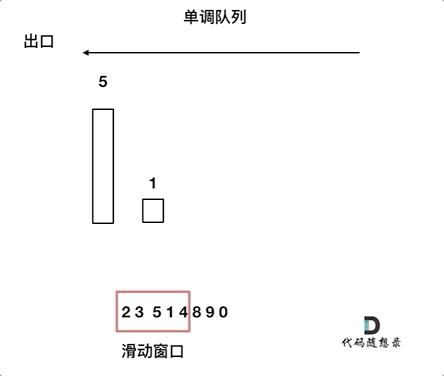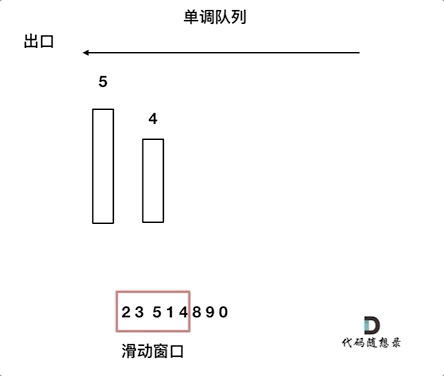
单调队列

维护一个只能单调增加/减少的队列，队列的front值一定是最大/最小值

img

对于窗口里的元素{2, 3, 5, 1 ,4}，单调队列里只维护{5, 4} 就够了，保持单调队列里单调递减，此时队列出口元素就是窗口里最大元素。

设计单调队列的时候，pop，和push操作要保持如下规则：

  1. pop(value)：如果窗口移除的元素value等于单调队列的front元素，那么队列弹出元素，否则不用任何操作（滑动窗口在右移时需要用到pop，此时只能pop出最大/小值，因为非“最大/最小”值都已经不在这个队列里的）
  2. push(value)：如果push的元素value大于tail元素的数值，那么就将队列tail的元素弹出，直到push元素的数值小于等于队列tail元素的数值为止；保证如果value是最大/最小值，则value一定会在front

保持如上规则，每次窗口移动的时候，只要问que.front()就可以返回当前窗口的最大值。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from collections import deque

class myQueue():
        def __init__(self,):
            self.que = deque()
        def push(self, value):
            print(self.que)
            # 若value大于que的tail值，需要不断tail值弹出，保证如果value是最大/最小值，则value一定会在front
            while self.que and value > self.que[-1]:
                self.que.pop()
            self.que.append(value)
        def pop(self, value):
            print(self.que)
            # 判断value是否等于front值，如果相等则弹出
            if self.que and value == self.que[0]:
                self.que.popleft()
        def front(self):
            # 返回队列前端(即最大值)
            return self.que[0]

239. 滑动窗口最大值

https://leetcode.cn/problems/sliding-window-maximum/

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

1
2
3
4
5
6
7
8
9
10
11
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：

1
2
输入：nums = [1], k = 1
输出：[1]

提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104
  • 1 <= k <= nums.length

思路

  1. 需要使用单调队列

以题目示例为例，输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3，动画如下：

img

代码

  • 时间复杂度O(n) — nums 中的每个元素最多也就被 push_back 和 pop_back 各一次，没有任何多余操作，所以整体的复杂度还是 O(n)
  • 空间复杂度O(k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from collections import deque

class myQueue():
        def __init__(self,):
            self.que = deque()
        def push(self, value):
            print(self.que)
            # 若value大于que的tail值，需要不断tail值弹出，保证如果value是最大/最小值，则value一定会在front
            while self.que and value > self.que[-1]:
                self.que.pop()
            self.que.append(value)
        def pop(self, value):
            print(self.que)
            # 判断value是否等于front值，如果相等则弹出
            if self.que and value == self.que[0]:
                self.que.popleft()
        def front(self):
            # 返回队列前端(即最大值)
            return self.que[0]

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        que = myQueue()
        results = list()
        for i in range(k):
            que.push(nums[i])
        L = len(nums)
        results.append(que.front())
        for i in range(k, L):
            que.pop(nums[i - k])
            print(f"que.pop: {nums[i - k]}")
            que.push(nums[i])
            results.append(que.front())
        return results

347. 前 K 个高频元素

https://leetcode.cn/problems/top-k-frequent-elements/

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

1
2
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

示例 2:

1
2
输入: nums = [1], k = 1
输出: [1]

提示：

  • 1 <= nums.length <= 105
  • k 的取值范围是 [1, 数组中不相同的元素的个数]
  • 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

**进阶：**你所设计算法的时间复杂度 必须 优于 O(n log n) ，其中 n 是数组大小。

思路

  1. 要统计元素出现频率、对频率排序、找出前K个高频元素
  2. 其中，统计频率-----可以使用map完成；
  3. 对频率排序----则需要使用“优先级队列”：一个披着队列外衣的堆，因为优先级队列对外接口只是从队头取元素，从队尾添加元素，再无其他取元素的方式，看起来就是一个队列；而且优先级队列内部元素是自动依照元素的权值排列

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。所以大家经常说的大顶堆（堆头是最大元素），小顶堆（堆头是最小元素）

题目要求前 K 个高频元素—决定使用大顶堆还是小顶堆（因为需要将不需要的数据pop出去），如果使用大顶堆，定义一个大小为k的大顶堆，在每次移动更新大顶堆的时候，每次弹出都把最大的元素弹出去了，那么怎么保留下来前K个高频元素呢。

而且使用大顶堆就要把所有元素都进行排序，那能不能只排序k个元素呢？

所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

代码

  • 时间复杂度O(nlogk)
  • 空间复杂度O(k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import heapq
class Solution:
    def topKFrequent(self, nums: List[int], k: int) -> List[int]:
        map_ = {}
        L = len(nums)
        for i in range(L):
            map_[nums[i]] = map_.get(nums[i], 0) + 1
        
        pri_que = list()

        for key, freq in map_.items():
            # 将(freq, key)添加到pri_que，并且按freq从小到大排序，形成个小顶堆
            heapq.heappush(pri_que, (freq, key))
            # 超出k个则自动弹出，保证仅有k个高频元素在小顶堆中
            if len(pri_que) > k:
                heapq.heappop(pri_que)
        print(pri_que)
        
        results = [0] * k
        for i in range(k - 1, -1, -1):
            results[i] = heapq.heappop(pri_que)[1]
        
        return results