LeetCodeCampsDay15二叉树part03
涉及树的高度/深度求解,以及平衡二叉树的判断,完全二叉树求节点个数;
根节点到任意节点的路径/深度求解
平衡二叉树
https://leetcode.cn/problems/balanced-binary-tree/
给定一个二叉树,判断它是否是 平衡二叉树
示例 1:

1
2
| 输入:root = [3,9,20,null,null,15,7]
输出:true
|
示例 2:

1
2
| 输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
|
示例 3:
提示:
- 树中的节点数在范围
[0, 5000] 内
-104 <= Node.val <= 104
后序递归思路
这里强调一波概念:
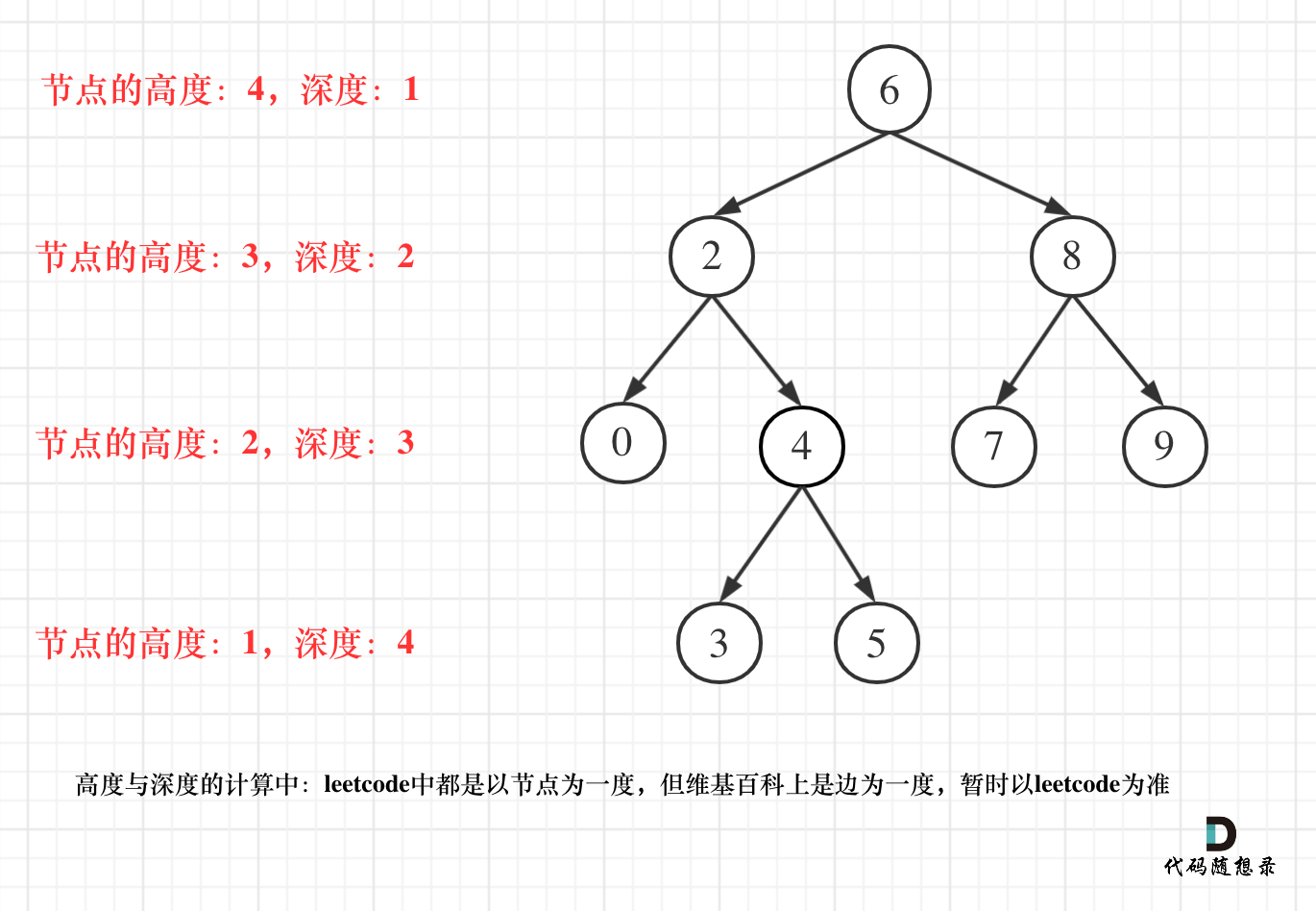
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:

如何判断一个树是不是平衡二叉树?—判断它的左树和右树的高度是否差大于1
使用递归+后序遍历方法
- 输入节点;输出高度(或者-1,表示高度差已经大于1了)
- 终止条件:节点为空返回0
- 单层逻辑:分别求左、右子树的高度,判断两者高度差,如果大于1则返回-1;否则返回1+max(左,右)
顺便提一下,在day14写过“求最大深度”,当时也使用后序递归算法;当时仅需要每个节点找到子树的深度,再加一即可
1
2
3
| leftDeepth = self.traverse(node.left)
rightDeepth = self.traverse(node.right)
return max(leftDeepth, rightDeepth) + 1
|
而现在需要求每个节点的子树高度,是同样的代码,因为求最大深度,即**“根节点的高度就是二叉树的最大深度”**
1
2
3
| leftHeight = self.getHeight(node.left)
rightHeight = self.getHeight(node.right)
return 1 + max(leftHeight, rightHeight)
|
但需要添加几个约束条件,比如求了leftH和righH后判断两者是否为-1,如果是,直接提前退出;以及判断两者高度差是否大于1
后序递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution:
def getHeight(self, node) -> int:
if not node:
return 0
leftHeight = self.getHeight(node.left)
if leftHeight == -1:
return -1
rightHeight = self.getHeight(node.right)
if rightHeight == -1:
return -1
if abs(leftHeight - rightHeight) > 1:
return -1
else:
return 1 + max(leftHeight, rightHeight)
def isBalanced(self, root: Optional[TreeNode]) -> bool:
res = self.getHeight(root)
if res != -1:
return True
return False
|
257. 二叉树的所有路径
https://leetcode.cn/problems/binary-tree-paths/
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:

1
2
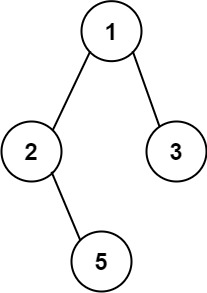
| 输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
|
示例 2:
提示:
- 树中节点的数目在范围
[1, 100] 内
-100 <= Node.val <= 100
思路
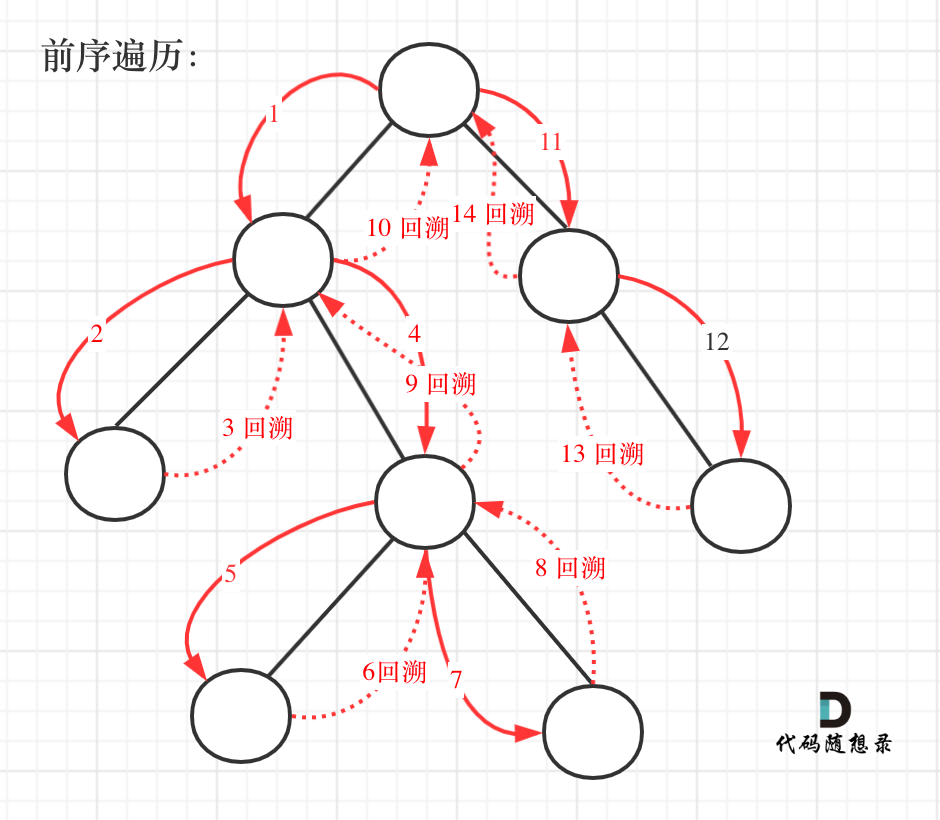
已知前序遍历是长这样的

还是按递归的方式写个前序,但终止条件有点儿不同,以往是判断node为空就直接返回,但这题目需要判断“如果当前节点为叶子节点”,就将根到节点的路径保存。所以,还需要有个path列表来记录路径,同时还需要个res列表记录所有从根节点到叶子节点的路径
于是,
- 递归的输入:node, path, res;输出就是res(用引用的方式输出就好)
- 终止条件:当前节点无孩子节点,则将当前的path添加到res里
- 单层逻辑:依然使用前序遍历,但需要添加判断条件,仅当left/right不为空时才能执行递归;而且递归后,需要将当前节点从path中弹出去
- 比如[1,2,3,null,5],当找到了path=[1,2,5]后,如果不把[2,5]弹出,下次path会记录成[1,2,5,3]而不是正确答案[1,3]
本题使用递归写简单直接一点儿,用迭代也可以完成
递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
class Solution:
def preOrder(self, node: TreeNode, path: list, res: list):
path.append(node.val)
if not node.left and not node.right:
s = ""
for i in range(len(path) - 1):
s += (str(path[i]) + "->")
s += str(path[-1])
res.append(s)
if node.left:
self.preOrder(node.left, path, res)
path.pop()
if node.right:
self.preOrder(node.right, path, res)
path.pop()
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
res = list()
path = list()
self.preOrder(root, path, res)
return res
|
迭代代码
迭代的过程更简单一点儿
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| stack = list()
path = list()
res = list()
stack.append(root)
path.append(str(root.val))
while stack:
node = stack.pop()
pathNode = path.pop()
if not node.left and not node.right:
res.append(pathNode)
if node.right:
stack.append(node.right)
path.append(pathNode + "->" + str(node.right.val))
if node.left:
stack.append(node.left)
path.append(pathNode + "->" + str(node.left.val))
return res
|
思考
day14以及day15中都有求二叉树的高度的题目(实现起来不难),并且有一个求最大深度的题目(但当时是直接用“根节点的高度“),但它规避了求某个节点所在深度的问题
深度的定义:指从根节点到该节点的最长简单路径边的长度
比如[3,9,20,7],其中7所在深度为3,对应的路径为[3,20,7]长度也为3
那么问题可以变成如何求根节点到任意节点的路径,思路可以和本题很像,这题目的终止条件是“遇到叶子节点”才把路径添加到res;而可以扩展成,遇到“target节点”就把路径添加到res
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode], target: Optional[TreeNode]) -> List[str]:
stack = list()
path = list()
res = list()
stack.append(root)
path.append(str(root.val))
while stack:
node = stack.pop()
pathNode = path.pop()
if node == target:
res.append(pathNode)
if node.right:
stack.append(node.right)
path.append(pathNode + "->" + str(node.right.val))
if node.left:
stack.append(node.left)
path.append(pathNode + "->" + str(node.left.val))
return res
so = Solution()
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
target = TreeNode(5)
root.left.left = target
print(so.binaryTreePaths(root, target))
|
输入root为[1,2,3,null,5],target为[5]
输出[‘1->2->5’],从而得知5的深度为3
404. 左叶子之和
https://leetcode.cn/problems/sum-of-left-leaves/
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:

1
2
3
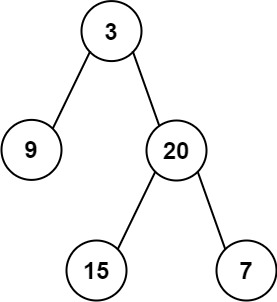
| 输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
|
示例 2:
提示:
- 节点数在
[1, 1000] 范围内
-1000 <= Node.val <= 1000
递归思路
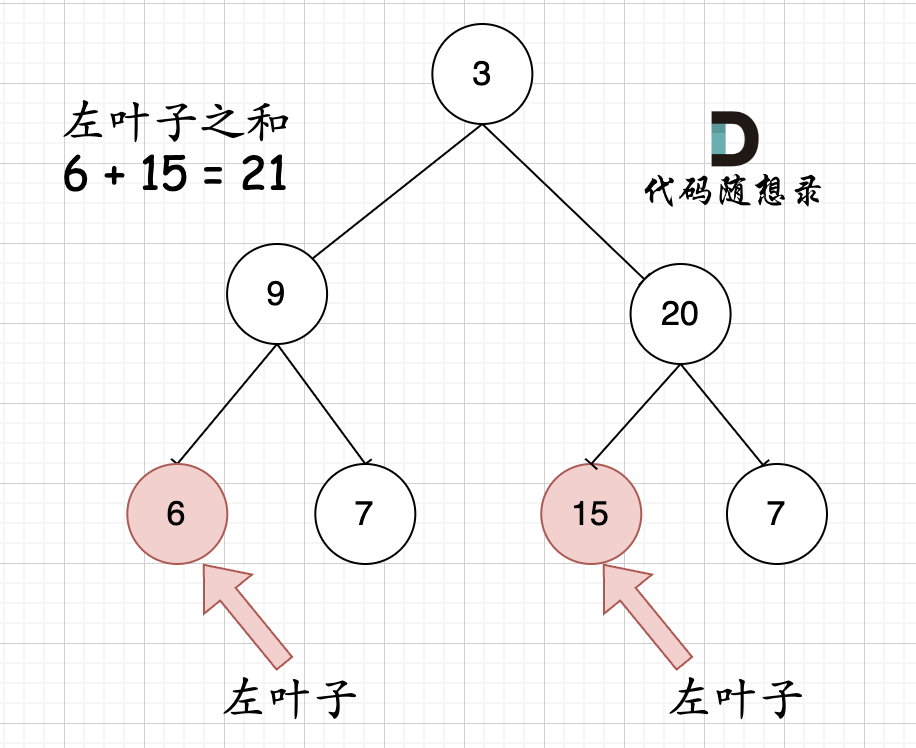
这题目要求是求“左子树之和”,如图所示;

可以使用递归的后序遍历
- 终止条件:if not node: return 0
- 输入输出:输入为node,输出为int,表示当前节点的左叶子之和
- 单层递归逻辑:求左子树的左叶子和、右子树的左叶子之和,再将两者相加,得到了当前节点的左叶子之和(这也是使用后序遍历的原因)
但有个不同点,如何判断当前节点是父节点的左叶子;
可以当父节点是当前节点时,判断node.left.left和node.left.right是否为空,判断当前的左子节点是否为空,如果其左子节点是叶子,则当前节点的左子树之和就是node.left.val
递归代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
class Solution:
def postOrder(self, node: TreeNode) -> int:
if not node:
return 0
if not node.left and not node.right:
return 0
sumOfLeft = self.postOrder(node.left)
if node.left:
if not node.left.left and not node.left.right:
sumOfLeft = node.left.val
sumOfRight = self.postOrder(node.right)
return sumOfLeft + sumOfRight
def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
return self.postOrder(root)
|
迭代思路
- 仍然使用后序遍历,注意入栈时,先中、再右、最后左,这样才能让出栈时的顺序为“左、右、中”
- 迭代的过程看着更简单一点儿
- 使用前序/中序也可以完成任务,而且这题目对实际顺序不敏感
- 比如入栈顺序为[中,右,左]、[中,左,右]、[左,中,右]、[右,中,左]、[左,右,中]、[右,左,中]都可以
迭代代码
- 时间复杂度O(N)
- 空间复杂度O(H),最坏O(N),最好O(logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
stack = list()
if not root:
return 0
stack.append(root)
sumLeftLeaves = 0
while stack:
node = stack.pop()
if node.left and not node.left.left and not node.left.right:
sumLeftLeaves += node.left.val
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return sumLeftLeaves
|
这题目使用前序也可以,如果使用栈+迭代,最好从while的底层向上读代码来理解实际的输出顺序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| def sumOfLeftLeaves(self, root: Optional[TreeNode]) -> int:
stack = list()
if not root:
return 0
stack.append(root)
sumLeftLeaves = 0
while stack:
node = stack.pop()
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
if node.left and not node.left.left and not node.left.right:
sumLeftLeaves += node.left.val
return sumLeftLeaves
|
222. 完全二叉树的节点个数
https://leetcode.cn/problems/count-complete-tree-nodes/
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
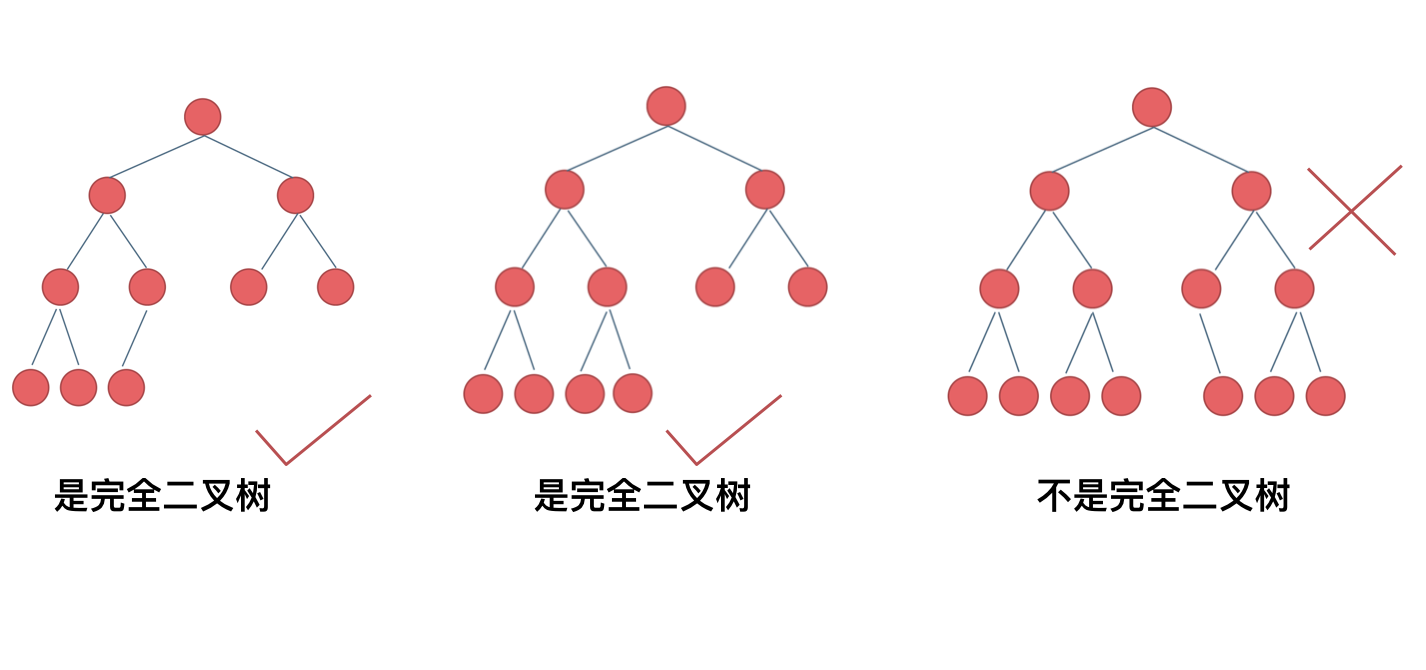
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(从第 0 层开始),则该层包含 1~ 2h 个节点。
示例 1:

1
2
| 输入:root = [1,2,3,4,5,6]
输出:6
|
示例 2:
示例 3:
提示:
- 树中节点的数目范围是
[0, 5 * 104]
0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
普通树处理思路
- 不管它是什么树,直接用前/中/后/层序遍历处理(递归)就行
- 递归输入:节点,输出:子树的节点个数
- 终止条件:节点为空返回0
- 单层逻辑:求左、右子树节点个数,再计算总和并加一
普通树的递归代码
- 时间复杂度O(N)
- 空间复杂度O(H) – 最坏O(N),最好O(logN)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution:
def postOrder(self, node: TreeNode) -> int:
if not node:
return 0
countOfLeft = self.postOrder(node.left)
countOfRight = self.postOrder(node.right)
return countOfLeft + countOfRight + 1
def countNodes(self, root: Optional[TreeNode]) -> int:
return self.postOrder(root)
|
普通树的迭代代码
使用前序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| def countNodes(self, root: Optional[TreeNode]) -> int:
stack = list()
if not root:
return 0
stack.append(root)
count = 0
while stack:
node = stack.pop()
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
count += 1
return count
|
使用层序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| def countNodes(self, root: Optional[TreeNode]) -> int:
from collections import deque
que = deque()
if not root:
return 0
que.append(root)
count = 0
while que:
node = que.popleft()
count += 1
if node.right:
que.append(node.right)
if node.left:
que.append(node.left)
return count
|
完成二叉树思路
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层,则该层包含 1~ 2^(h-1) 个节点。

完全二叉树只有两种情况,情况一:就是满二叉树,情况二:最后一层叶子节点没有满。
对于情况一,可以直接用 2^树深度 - 1 来计算,注意这里根节点深度为1。
对于情况二,分别递归左孩子,和右孩子,递归到某一深度一定会有左孩子或者右孩子为满二叉树,然后依然可以按照情况1来计算。
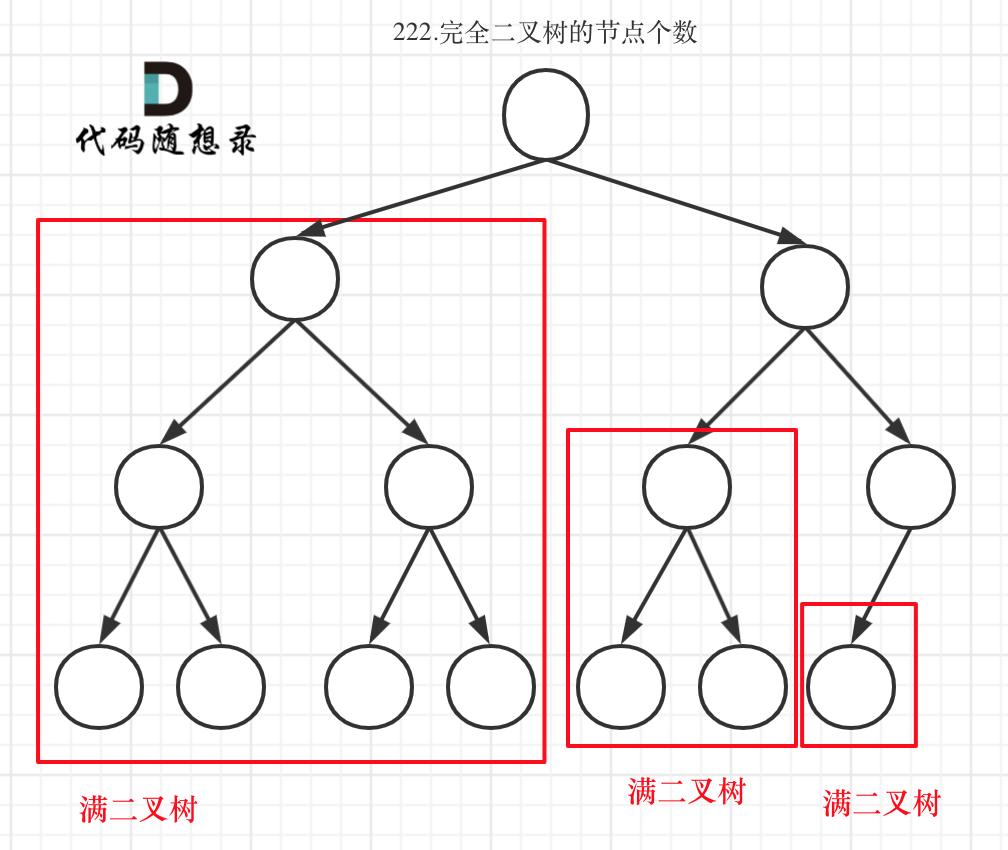
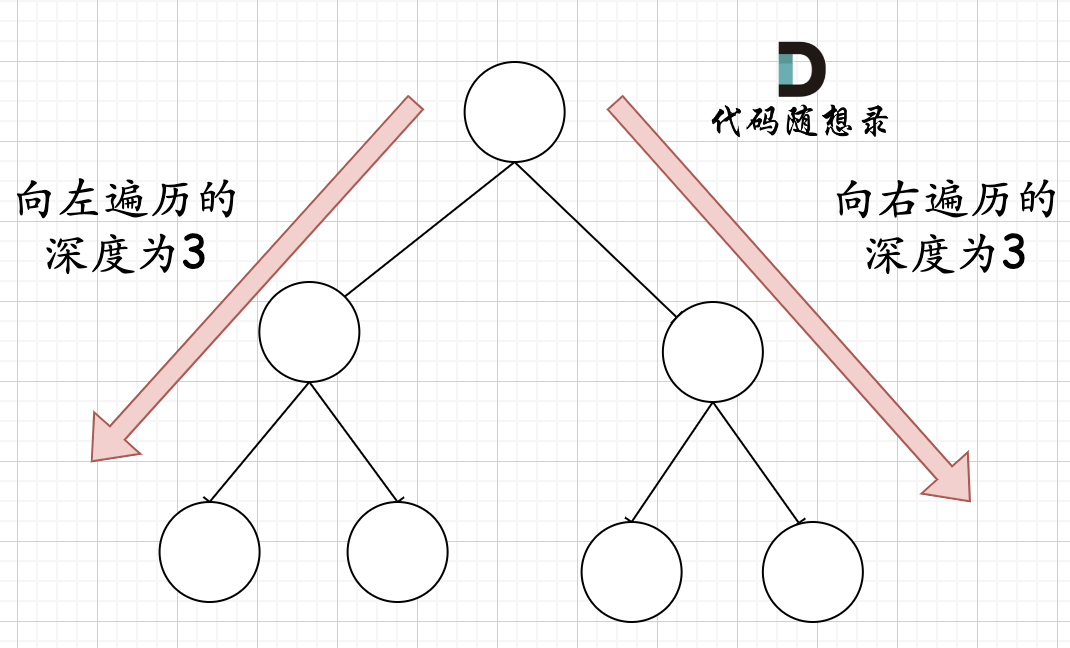
完全二叉树(一)如图:

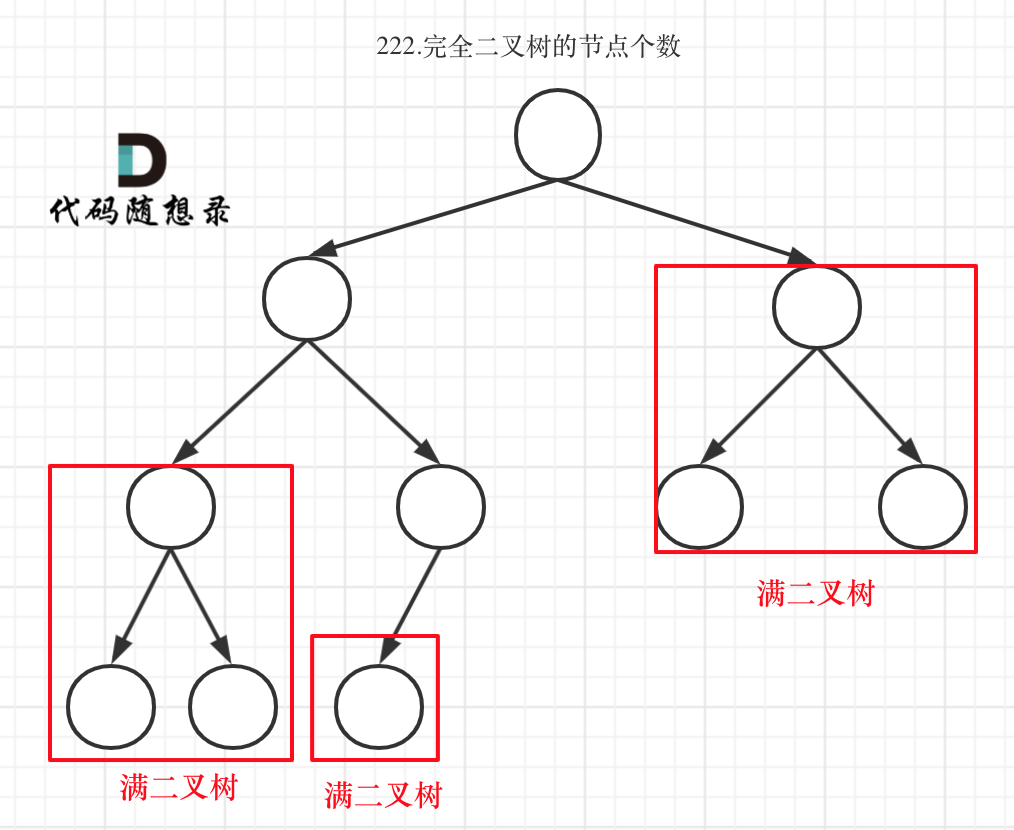
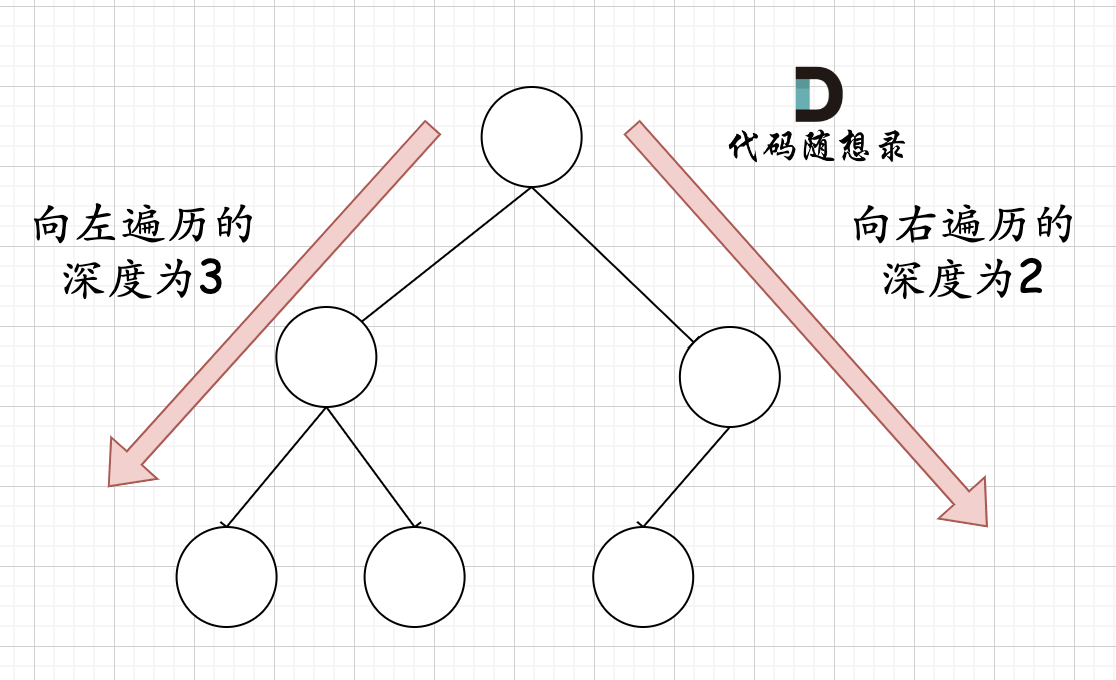
完全二叉树(二)如图:

可以看出如果整个树不是满二叉树,就递归其左右孩子,直到遇到满二叉树为止,用公式计算这个子树(满二叉树)的节点数量。
这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢? —如果递归向左遍历的深度等于递归向右遍历的深度,那说明就是满二叉树
顺便提一句,如何判断一个树是否为平衡二叉树?----判断左、右子树的高度差,如果高度差大于1则不是

下面这图中“向右遍历的深度为2”指的是,令rightNode = node.right,并且循环rightNode = rightNode.right并count+=1,一路向右,如果出现了“非满二叉树”就出出现深度为2,否则深度一定为3;就像左边一样
通过leftNode一路向左,rightNode一路向右,来判断子树的深度是否一样,是否是满二叉树
之所以能用leftNode一路向左,rightNode一路向右,也是利用了完全二叉树的性质

完全二叉树代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution:
def countNum(self, node: TreeNode) -> int:
if not node:
return 0
leftNode = node.left
rightNode = node.right
leftDepth = 0
rightDepth = 0
while leftNode:
leftNode = leftNode.left
leftDepth += 1
while rightNode:
rightNode = rightNode.right
rightDepth += 1
if leftDepth == rightDepth:
return (2 << leftDepth) - 1
leftNum = self.countNum(node.left)
rightNum = self.countNum(node.right)
return leftNum + rightNum + 1
def countNodes(self, root: Optional[TreeNode]) -> int:
return self.countNum(root)
|