LeetCodeCampsDay21二叉树part08

平衡二叉树的构造；修剪二叉树（难度甚至比删除二叉树的节点要简单一些）

669. 修剪二叉搜索树

https://leetcode.cn/problems/trim-a-binary-search-tree/

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

img

1
2
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

img

1
2
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

提示：

  • 树中节点数在范围 [1, 104] 内
  • 0 <= Node.val <= 104
  • 树中每个节点的值都是 唯一 的
  • 题目数据保证输入是一棵有效的二叉搜索树
  • 0 <= low <= high <= 104

递归思路

  1. 使用递归，带返回值，返回的是修剪后的子树节点；
  2. 输入节点/low以及high，输出是修剪后的子树节点；
  3. 终止条件，如果输入节点为空就返回
  4. 单层逻辑：修剪的规则是，如果node.val<low，则node需要被删除，并且node.right会被当成node返回给node的父节点（并且node.left肯定都小于low，都被修剪了）；如果node.val> high,，则node需要被删除，并且node.left会被当成node返回给node的父节点（并且node.right都大于high，都被修剪了）

递归代码

  • 时间复杂度O(N)
  • 空间复杂度O(H)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def foo(self, node, low, high) -> TreeNode:
        # 使用递归，带返回值，返回的是修剪后的子树节点
        if not node:
            return None
        
        if node.val < low:
            # 若node.val小于low，说明node是需要被删除的，但node.right可能不会被删除
            # 这里直接返回了node.right，说明node已经被修剪了
            return self.foo(node.right, low, high)
        if node.val > high:
            return self.foo(node.left, low, high)
        
        # 这里是将修剪好的子树上传上来
        node.left = self.foo(node.left, low, high)
        node.right = self.foo(node.right, low, high)

        return node

    def trimBST(self, root: Optional[TreeNode], low: int, high: int) -> Optional[TreeNode]:
        # 使用递归完成
        return self.foo(root, low, high)

108. 将有序数组转换为二叉搜索树

https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡 二叉搜索树。

示例 1：

img

1
2
3
输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

示例 2：

img

1
2
3
输入：nums = [1,3]
输出：[3,1]
解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

递归思路

  1. 使用递归，带返回值，输出排序后的子树节点
  2. 输入num(list)，输出这个nums的树
  3. 终止条件num为空
  4. 单层逻辑：先找到这个nums里的medium值（就是len(nums)//2），如果len为偶数，选择哪个都可以；以这个medium为root，然后递归地构造root的左、右子树；这个方法与之前构造最大子树（654. 最大二叉树）有点像。

递归代码

  • 时间复杂度O(N)
  • 空间复杂度O(H)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    # 找到中间位置的节点当成root，再以中间节点划分左、右区间进行递归地建树
    def foo(self, nums: List[int]) -> TreeNode:
        if len(nums) == 0:
            return None
        
        L = len(nums)
        midIndex = L // 2
        root = TreeNode(nums[midIndex])
        root.left = self.foo(nums[:midIndex])
        root.right = self.foo(nums[midIndex + 1:])
        return root

    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        # 递归
        return self.foo(nums)

538. 把二叉搜索树转换为累加树

https://leetcode.cn/problems/convert-bst-to-greater-tree/

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

**注意：**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

示例 1：

img

1
2
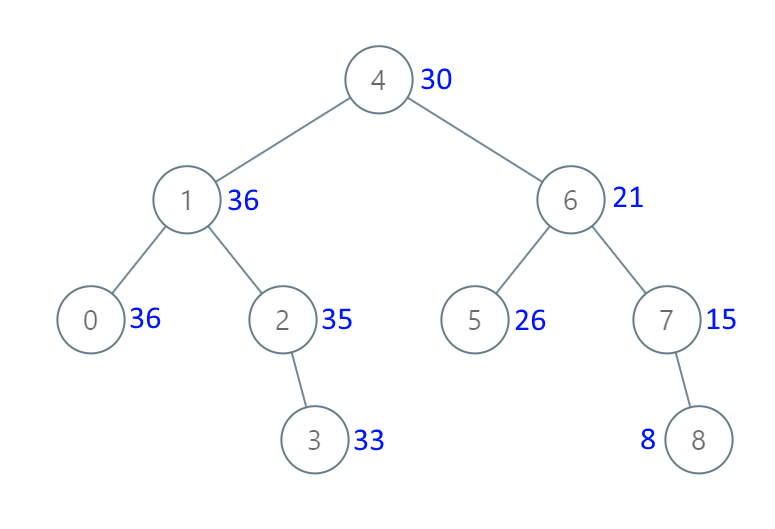
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

1
2
输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

1
2
输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

1
2
输入：root = [3,2,4,1]
输出：[7,9,4,10]

提示：

  • 树中的节点数介于 0 和 104 之间。
  • 每个节点的值介于 -104 和 104 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

递归思路

因为本题为BST，它本身就有了顺序，可以先做一次反中序遍历，再将中间节点更新为node.val += pre.val，其中pre.val就是反中序遍历中较大的节点的累加值

  1. 使用不带返回值的递归
  2. 输入node节点，无输出
  3. 终止条件，当前节点为空，直接返回
  4. 单层逻辑：使用反中序遍历，对中间节点进行更新，更新成node.val = node.val + pre.val

递归代码

  • 时间复杂度O(N)
  • 空间复杂度O(H)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.pre = TreeNode(0)

    def foo(self,  node):
        if not node:
            return 
        
        if node.right:
            self.foo(node.right)
        node.val += self.pre.val
        self.pre = node
        if node.left:
            self.foo(node.left)

    def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        # 思路1 把中序遍历，逐个累加，需要有个pre节点
        
        self.foo(root)
        return root

迭代思路

  1. 使用反中序遍历，先一路干到最右节点（把一路上的节点都添加到stack中），再逐个弹出，弹出的顺序就是（右、中、左）即完成反中序遍历；对中间节点进行操作，修改它的值为node.val += pre.val（注意，从python机制上来说，使用+=是原地赋值而使用val = val + pre会新增空间）

迭代代码

  • 时间复杂度O(N)
  • 空间复杂度O(H)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
    # 思路1 把中序遍历，逐个累加，需要有个pre节点
    
    # self.foo(root)
    # return root

    # 使用栈+迭代实现反中序遍历
    stack = list()
    if not root:
        return root
    cur = root
    pre = TreeNode(0)
    while stack or cur:
        if cur:
            stack.append(cur)
            # 先干到最右节点
            cur = cur.right
        else:
            # 最右节点
            cur = stack.pop()
            # 中节点
            cur.val += pre.val
            pre = cur
            # 左节点
            cur = cur.left
    
    return root