LeetCodeCampsDay22回溯part01

包含回溯基础内容，虽然和递归还有点儿像的哦

理论基础

什么是回溯法

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

在二叉树系列中，我们已经不止一次，提到了回溯，例如二叉树：以为使用了递归，其实还隐藏着回溯 (opens new window)。

回溯是递归的副产品，只要有递归就会有回溯。

所以以下讲解中，回溯函数也就是递归函数，指的都是一个函数

在递归中必有回溯，只是之前都没有用到回溯的操作

回溯法的效率

回溯法的性能如何呢，这里要和大家说清楚了，虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

此时大家应该好奇了，都什么问题，这么牛逼，只能暴力搜索

如何理解回溯法

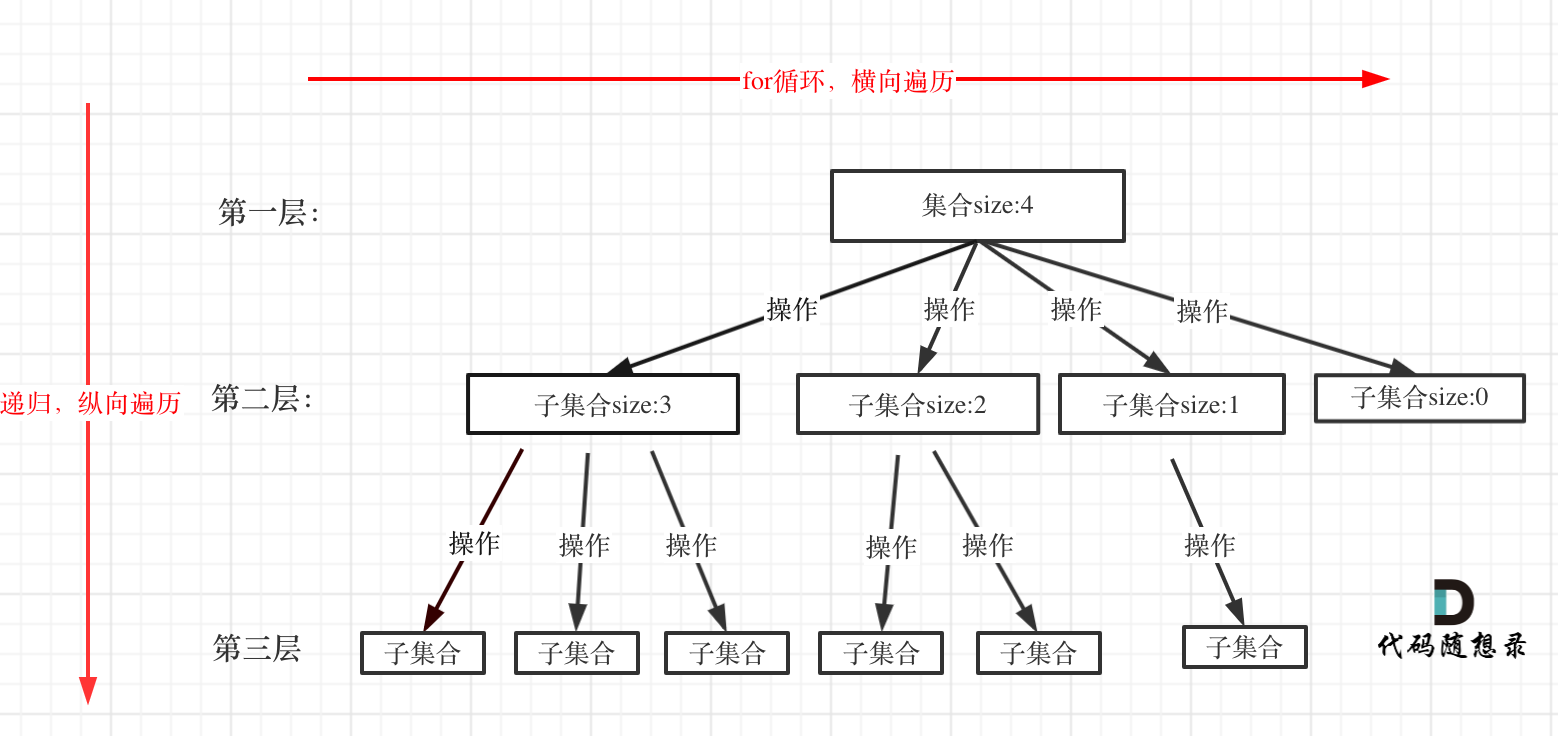
回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度就构成了树的深度。

递归就要有终止条件，所以必然是一棵高度有限的树（N叉树）。

这块可能初学者还不太理解，后面的回溯算法解决的所有题目中，我都会强调这一点并画图举相应的例子，现在有一个印象就行。

回溯模板

  1. 确定回溯的输入与输出值（是否有返回值）
  2. 终止条件（必有）
  3. 单层逻辑，在回溯里的单层逻辑往往需要使用for循环（横向遍历），这里的横向遍历是指单层逻辑需要处理的事儿

回溯函数代码

1
void backtracking(参数)

终止条件代码

1
2
3
4
if (终止条件) {
    存放结果;
    return;
}

单层逻辑代码

1
2
3
4
5
for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

比如下面的例子里，递归是用来纵向遍历，而for遍历是单层逻辑里的横向遍历（注意回溯本身就是暴力搜索，或者说本身就是一堆for循环的变体）

for循环就是遍历子集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次

img

77. 组合

https://leetcode.cn/problems/combinations/

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

1
2
3
4
5
6
7
8
9
10
输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

1
2
输入：n = 1, k = 1
输出：[[1]]

提示：

  • 1 <= n <= 20
  • 1 <= k <= n

回溯思路

输入：n = 100, k = 3 那么就三层for循环，代码如下

1
2
3
4
5
6
7
8
int n = 100;
for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
        for (int u = j + 1; u <= n; n++) {
            cout << i << " " << j << " " << u << endl;
        }
    }
}

但如果n=100, k = 50，此时需要写50个for循环吗？大可不必，使用回溯即可替代这么多for循环操作

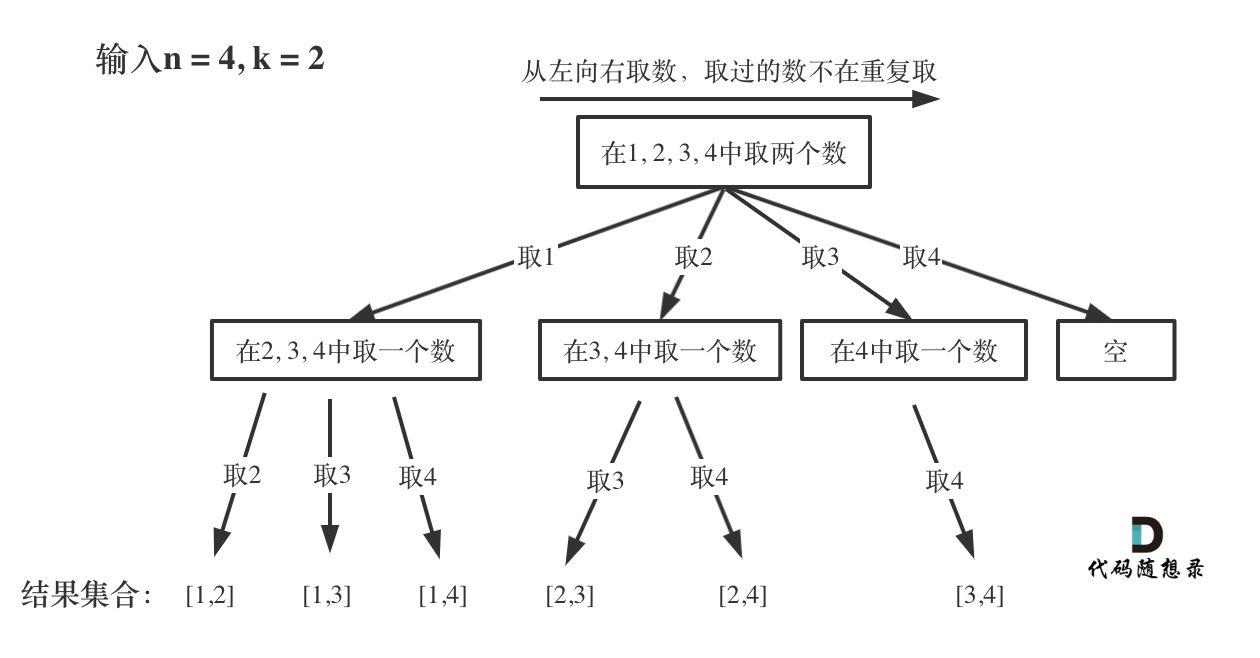
将这个问题抽象出来，把它使用树进行展开，每个问题解构成子问题，则(1,2,3,4)的一个子树为(2,3,4)，(3,4), (4), ()；而所谓得到k集合，就是将取出来的数添加到path中；有点儿像257. 二叉树的所有路径；

注意点一：如果子树里也是(1,2,3,4), (1,2,3,4), (1,2,3,4), (1,2,3,4)则得到的全排列，但题目里要求的是组合，比如(1,2)和(2,1)被认为一个组合，且组合里的数字只能使用一次

img

回溯代码

  • 时间复杂度O(C(n,k)*k)
  • 空间复杂度O(C(n,k)*k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def __init__(self):
        self.res = list()
        self.path = list()

    def foo(self, n: int, k: int, start = 1):
        if len(self.path) == k:
            # 注意这里不能只用append(self.path),必须使用self.path[:],否则最终输出的self.res为空
            # 如果直接使用 ⁠self.path，你实际上是在向 ⁠self.res 中添加一个对 ⁠self.path 列表的引用
            # 而不是列表的副本。这会导致后续对 ⁠self.path 的修改影响到已经添加到 ⁠self.res 中的元素，从而导致结果错误。
            self.res.append(self.path[:])
            return 
        
        for i in range(start, n + 1):
            self.path.append(i)
            self.foo(n, k, i + 1)
            self.path.pop()
        

    def combine(self, n: int, k: int) -> List[List[int]]:
        self.foo(n, k, 1)
        return self.res

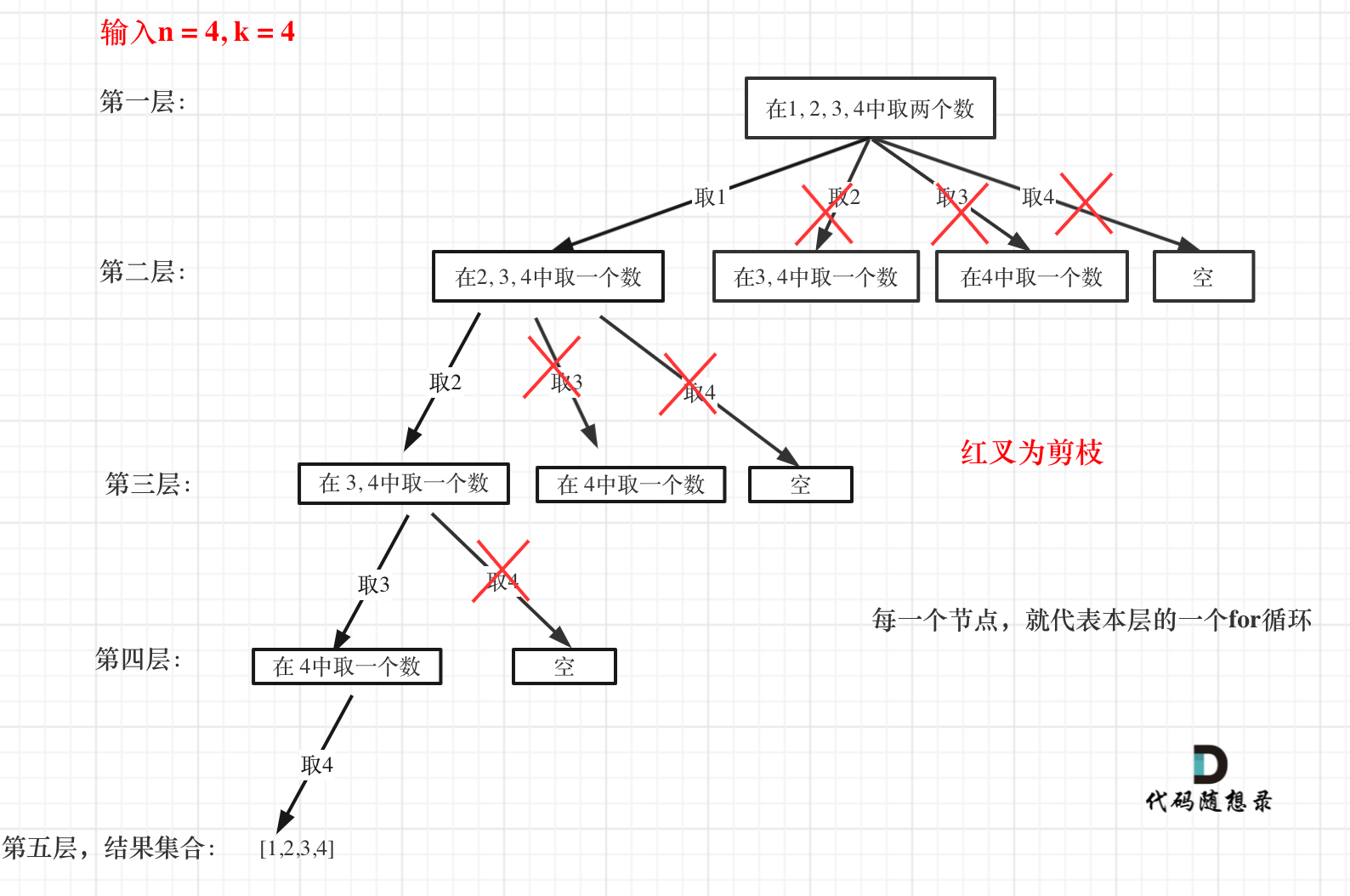
剪枝操作

添加一个判断，如果k大于n - i + 1 + len(self.path) ，说明后面的组合数量不可能满足k个，直接剪掉

img

包含剪枝的代码

  • 时间复杂度O(C(n, k) * k)
  • 空间复杂度O(C(n, k)* k + k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution:
    def __init__(self):
        self.res = list()
        self.path = list()

    def foo(self, n: int, k: int, start = 1):
          
        if len(self.path) == k:
            # 注意这里不能只用append(self.path),必须使用self.path[:],否则最终输出的self.res为空
            # 如果直接使用 ⁠self.path，你实际上是在向 ⁠self.res 中添加一个对 ⁠self.path 列表的引用
            # 而不是列表的副本。这会导致后续对 ⁠self.path 的修改影响到已经添加到 ⁠self.res 中的元素，从而导致结果错误。
            self.res.append(self.path[:])
            return 
        
        for i in range(start, n + 1):
       			# 剪枝操作
            if k > n - i + 1 + len(self.path):
                break
            self.path.append(i)
            self.foo(n, k, i + 1)
            self.path.pop()
        

    def combine(self, n: int, k: int) -> List[List[int]]:
        self.foo(n, k, 1)
        return self.res

216. 组合总和 III

https://leetcode.cn/problems/combination-sum-iii/

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

1
2
3
4
5
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

1
2
3
4
5
6
7
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

1
2
3
4
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

  • 2 <= k <= 9
  • 1 <= n <= 60

回溯代码

  • 时间复杂度O(C(9,k)*k)
  • 空间复杂度O(C(9,k)*k + k)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution:
    def __init__(self):
        self.res = list()
        self.path = list()

    def foo(self, k: int, n: int, end = 9, start = 1):
        if len(self.path) == k:
            if sum(self.path[:]) == n:
                self.res.append(self.path[:])
                return
        elif len(self.path) > k:
            return
        
        for i in range(start, end + 1):
            # 剪枝一，按个数剪枝
            if k > n - i + 1 + len(self.path):
                break
            # 剪枝二，按path的和判断，如果已经大于n，则必须不成立
            if sum(self.path[:]) > n:
                break
            self.path.append(i)
            self.foo(k, n, end, i + 1)
            self.path.pop()
        

    def combinationSum3(self, k: int, n: int) -> List[List[int]]:
        # 使用递归，思路和组合1有点儿像，但这次需要将所有的数字仍放在path中
        # 判断sum of path是否等于n，如果等于n则添加到res
        self.foo(k, n)

        return self.res

17. 电话号码的字母组合

https://leetcode.cn/problems/letter-combinations-of-a-phone-number/

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

img

示例 1：

1
2
输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

1
2
输入：digits = ""
输出：[]

示例 3：

1
2
输入：digits = "2"
输出：["a","b","c"]

提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。

回溯思路

先构建个alphaB = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]

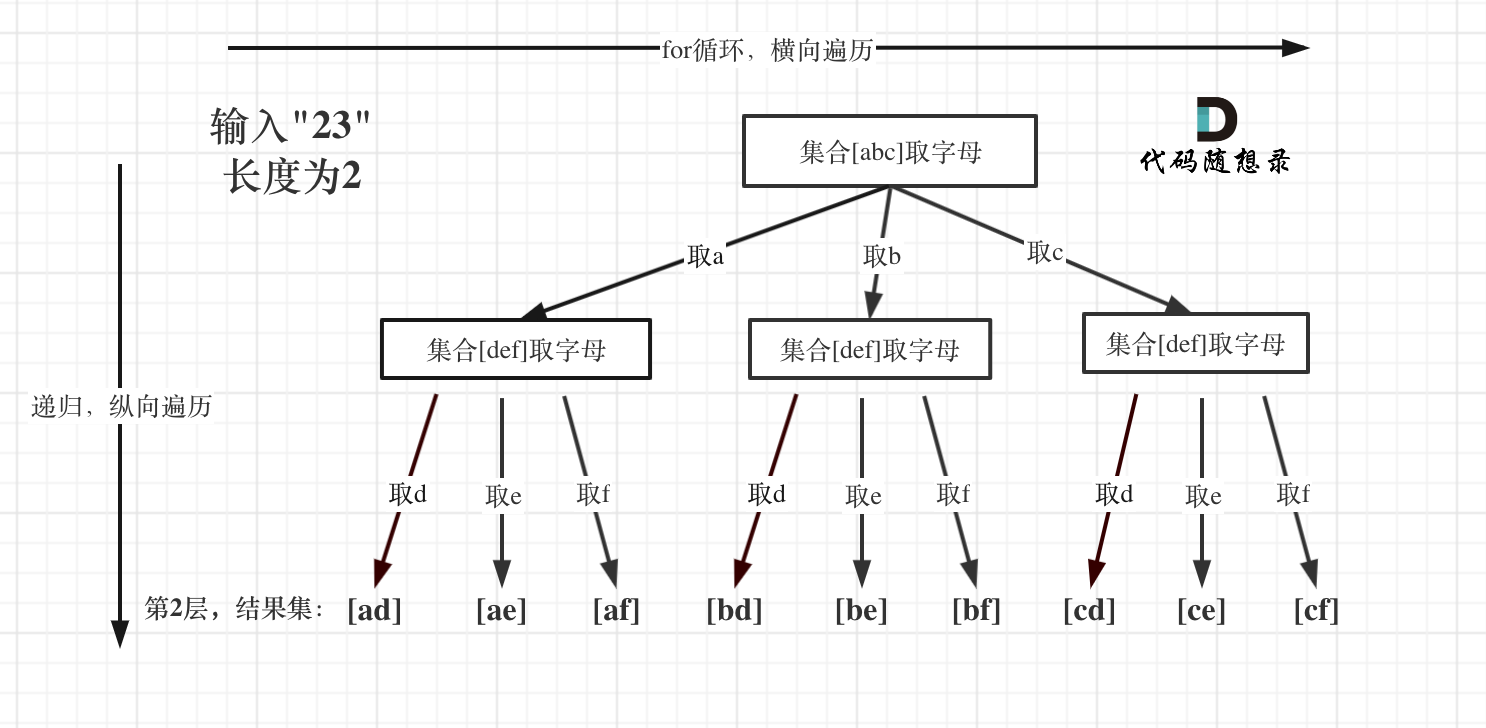
比如digits=“623”，则

  1. 与前面两个相似，纵向的遍历是6->2->3；而第一层是mno，第二层是"abc", “abc”, “abc”，第三层是九个"def"
  2. 回溯输入digits以及在digits开始的下标，无返回值
  3. 终止条件：如果start大于等于len(digits)说明已经遍历完了，此时若self.path不为空，则添加到self.res里
  4. 单层逻辑：先从alphaB取出当前digits[start]对应数字的字母表，对逐个字母遍历并添加到path里，再递归到下一个digit，最终再path弹出之前添加的字母
    1. 比如6->‘mno’，对’mno’进行遍历；将m添加到path里，然后递归到digits[start+1]，即2->‘abc’，再对’abc’遍历，将a添加到path里，此时path长度等于digits长度，将’ma’添加到res并退出；此时回溯，path弹出’a’，再将b添加到path里，重复……

img

回溯代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def __init__(self):
        self.alphaB = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
        self.path = list()
        self.res = list()

    def foo(self, digits, start):
        if len(path) == len(digits) or start >= len(digits):
            res = "".join(self.path[:])
            if res != "":
                self.res.append(res)
            return
        for i in self.alphaB[int(digits[start])]:
            self.path.append(i)
            self.foo(digits, start + 1)
            self.path.pop()

    def letterCombinations(self, digits: str) -> List[str]:
        # 递归
        self.foo(digits, 0)        
        return self.res