LeetCodeCampsDay23回溯part02
LeetCodeCampsDay23回溯part02
40.组合总和2使用了去重复的技巧,而131分割回文串是每次向path添加多个元素的类型
39.和40都是每次向path添加一个元素的类型;
39. 组合总和
https://leetcode.cn/problems/combination-sum/
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
1 | 输入:candidates = [2,3,6,7], target = 7 |
示例 2:
1 | 输入: candidates = [2,3,5], target = 8 |
示例 3:
1 | 输入: candidates = [2], target = 1 |
提示:
1 <= candidates.length <= 302 <= candidates[i] <= 40candidates的所有元素 互不相同1 <= target <= 40
回溯思路
- 和
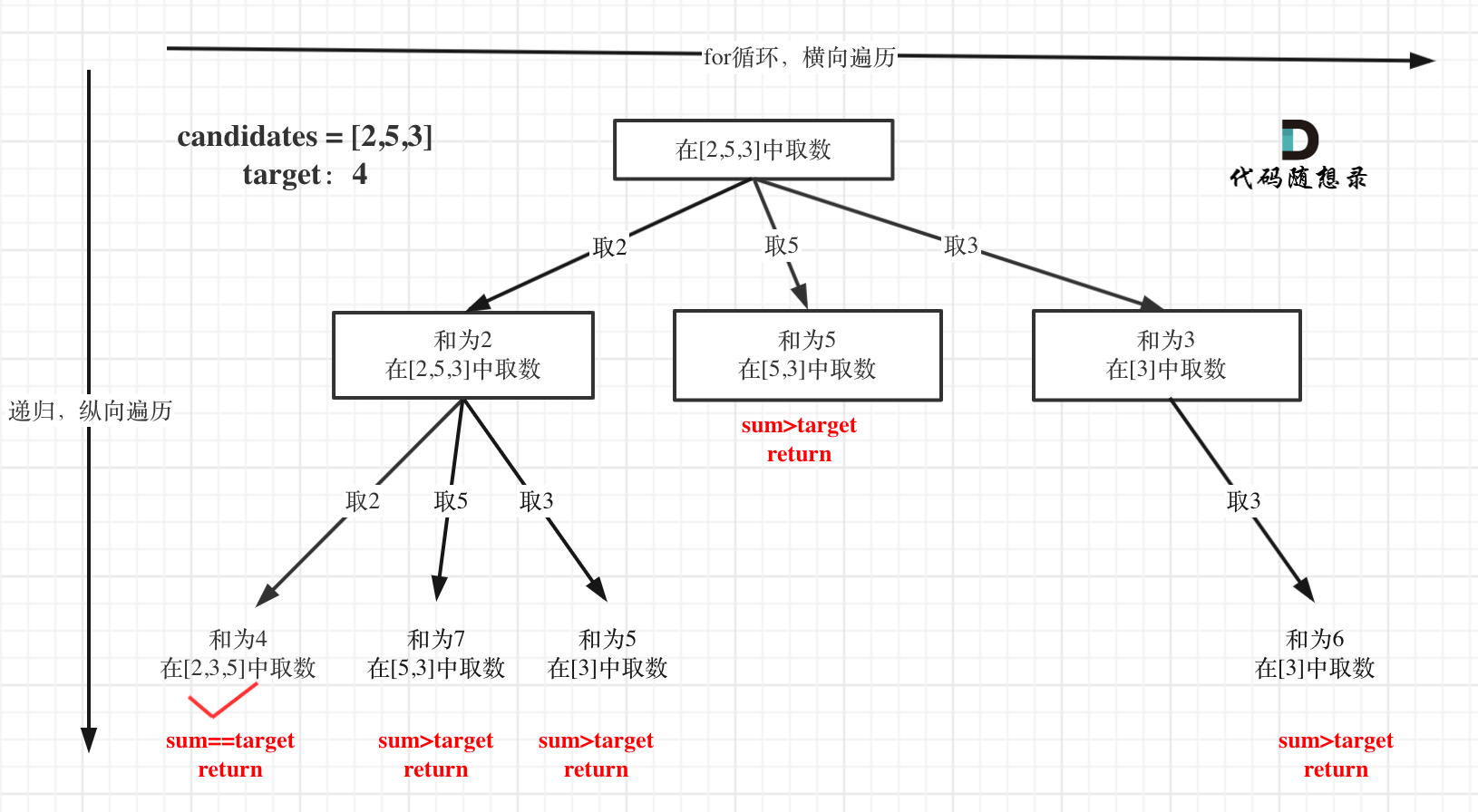
77组合,以及216.组合总和III很像,唯一区别是start位置,在77组合里,每层for循环里的下一个递归函数start为i+1,而这题目里下一个递归函数start为i即可;同样使用一个path记录路径,必要时计算path的和 - 输入一个候选列表,目标值,以及开始位置of候选列表
- 终止条件:sum of path如果大于target则终止;如果等于target则res添加path
- 单层逻辑:把当前值添加到path,递归下一轮(注意start需要包含当前值),再让path将当前值弹出
如果,start值一直是0,会得到如[2,2,3],[3,2,2]这种重复的结果(注意题目要求不包含重复的组合)
回溯代码
- 时间复杂度O(N * 2 ^ T)
- 空间复杂度O(T)
1 | class Solution: |
40. 组合总和 II
https://leetcode.cn/problems/combination-sum-ii/
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
**注意:**解集不能包含重复的组合。
示例 1:
1 | 输入: candidates = [10,1,2,7,6,1,5], target = 8, |
示例 2:
1 | 输入: candidates = [2,5,2,1,2], target = 5, |
提示:
1 <= candidates.length <= 1001 <= candidates[i] <= 501 <= target <= 30
回溯思路
本题目前一题目有点儿像,但不同点在于:本题要求不能有相同组合,第一想法是使用字典或set排队重复元素,但这样会导致超时(比如[1,1,1,1,…,1], target=30会发生超时);所以需要在每层处理时就进行去重复,注意,下面的方法必须先对数组排序
- 输入还是candidates和target,以及start节点;
- 终止条件:sumOfPath > target则退出,等于target则添加到res;
- 单层逻辑:[剪枝]若sumOfPath + candidates[i]大于target则遍历下一个元素(或者直接return, 如果candiates已经排序过了),判断candidates[i - 1] == candidates[i],目的是防止相同的元素再参与,注意只要使用continue即可,别使用return或break,因为后面还需要继续遍历
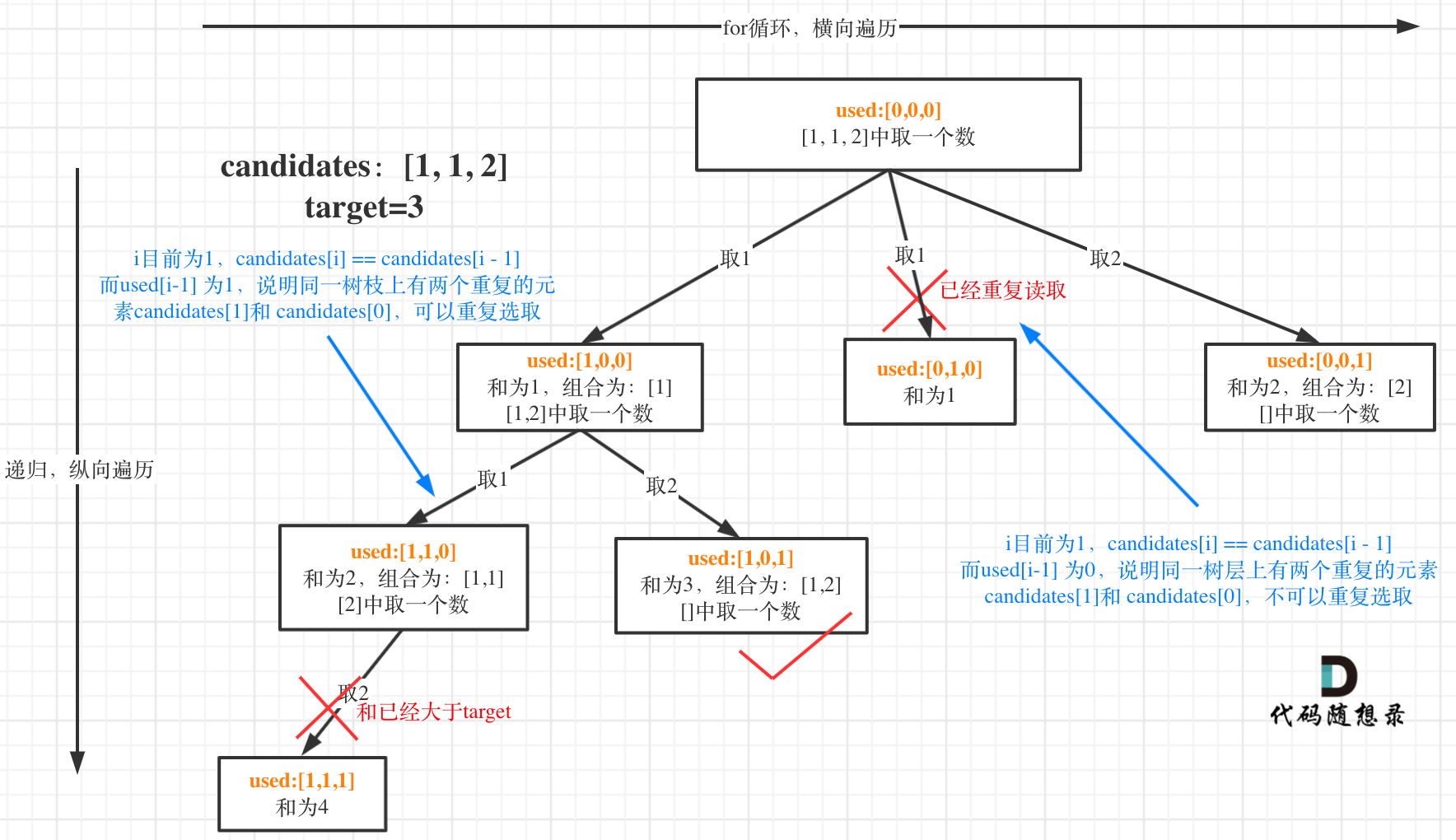
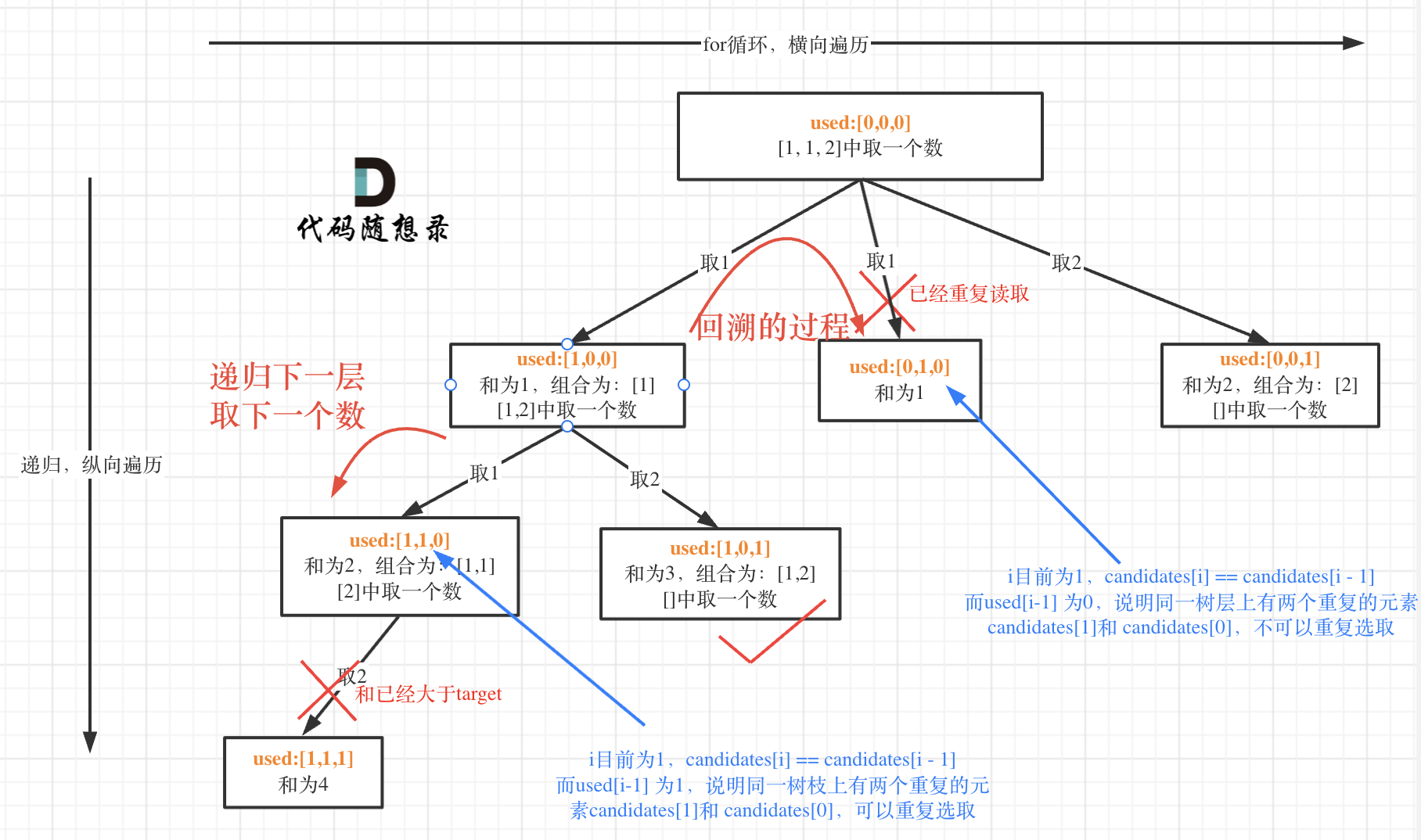
下面这图的重点是:同一层如果有重复元素就不重复选取了,而不同层如果有重复元素是可以重复选的;比如[1,1,1,1,1,…,1],target=30,对第一个1来说,后面的[1,1,1,1…,1]都可以选;而对第二个1来说
我在图中将used的变化用橘黄色标注上,可以看出在candidates[i] == candidates[i - 1]相同的情况下:
- used[i - 1] == true,说明同一树枝candidates[i - 1]使用过
- used[i - 1] == false,说明同一树层candidates[i - 1]使用过
可能有的录友想,为什么 used[i - 1] == false 就是同一树层呢,因为同一树层,used[i - 1] == false 才能表示,当前取的 candidates[i] 是从 candidates[i - 1] 回溯而来的。
而 used[i - 1] == true,说明是进入下一层递归,去下一个数,所以是树枝上,如图所示:
注意,下面的方法必须先对数组排序
注意,下面的方法必须先对数组排序
注意,下面的方法必须先对数组排序
相似的题目还有90.子集II
回溯代码
- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n)
1 | class Solution: |
131. 分割回文串
https://leetcode.cn/problems/palindrome-partitioning/
给你一个字符串 s,请你将 s 分割成一些 子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
示例 1:
1 | 输入:s = "aab" |
示例 2:
1 | 输入:s = "a" |
提示:
1 <= s.length <= 16s仅由小写英文字母组成
回溯思路
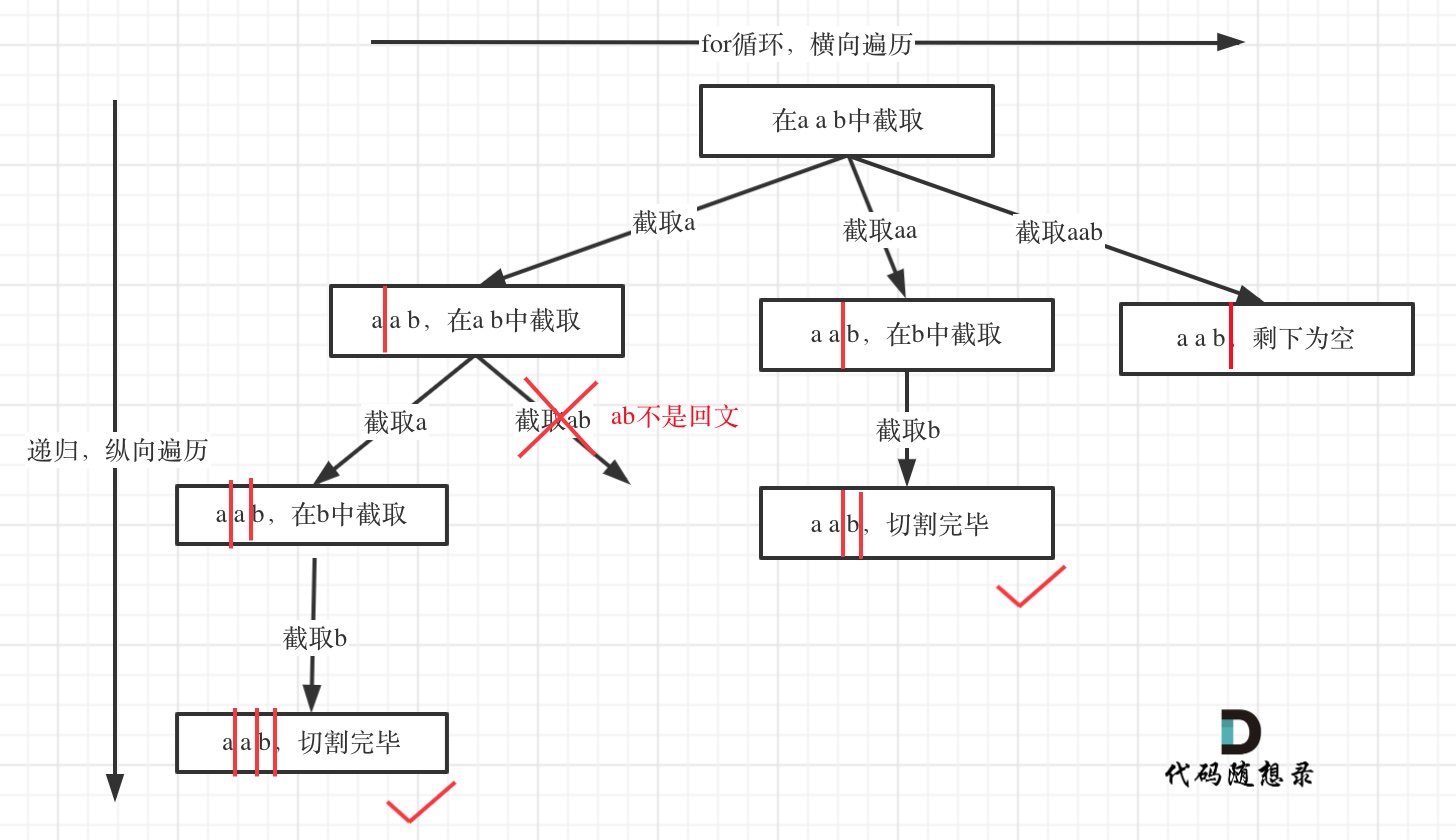
注意给的示例s=‘aab’的输出是[[“a”,“a”,“b”],[“aa”,“b”]],可以看出来是先将’a’添加到path,再分别把’a’和’b’添加到path;每个次是先将’aa’添加到path,再将’b’添加到path;说明一点,横向上的startIndex是向右增加的,而纵向上,先处理’a’,再处理’a’的子串’ab’
本题里仍使用回溯算法,其中,横向遍历(for循环)需要判断s[start:i+1]这段子串是否是回文的,比如第一次for循环执行:‘a’, ‘aa’, ‘aab’,如果’a’是回文的,才对后面的’ab’进行递归,去处理子段;
回溯代码
- 时间复杂度: O(n * 2^n)
- 空间复杂度: O(n^2)
1 | class Solution: |