LeetCodeCampsDay24回溯part03

再次使用了去重复的技巧，其中78,90两题目像是77.组合的变体，都是每次向path添加一个元素的类型；

而93 复原ip以及131. 分割回文串都是每次向path添加多个元素的类型

93. 复原 IP 地址

https://leetcode.cn/problems/restore-ip-addresses/

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

  • 例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

示例 1：

1
2
输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

1
2
输入：s = "0000"
输出：["0.0.0.0"]

示例 3：

1
2
输入：s = "101023"
输出：["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]

提示：

  • 1 <= s.length <= 20
  • s 仅由数字组成

回溯思路

本题难度还是有的，但在做了131.分割回文串 后，会发现这两个题目思路是相似的

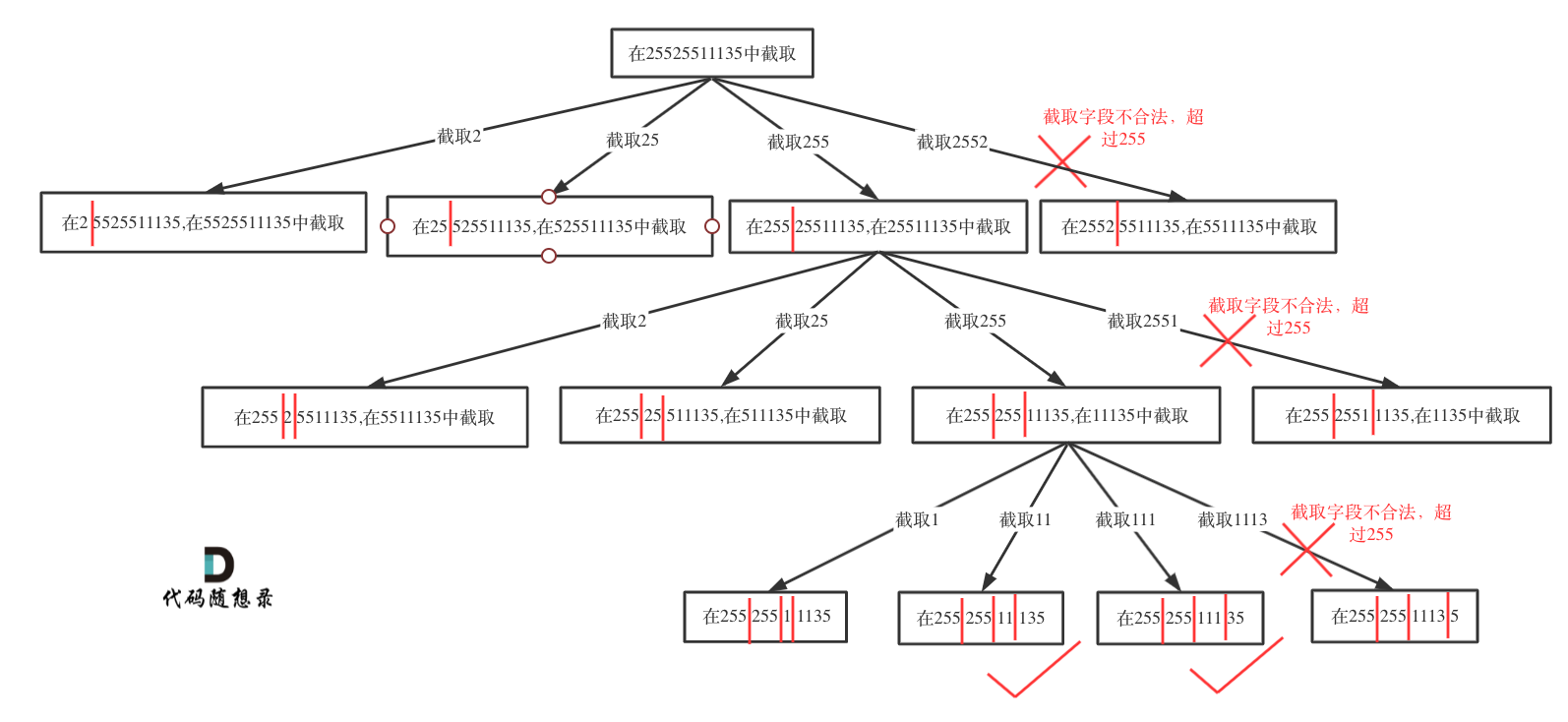
在131.里，需要先在for循环里判断 s[start, i+1]是否是回文串，如果是再添加到path里；而这题目也是如此，先判断s[start, i+1]是否是合规的数字（比如数字不大于255，如果0开头则必须只能有0，数字长度不大于4）；如果合规，再将数字添加到path里，再纵向搜索，再弹出以回溯；

  1. 输入输出：输入字符串，以及startIndex, 和深度（因为ip最多四个整数，所以深度只有4，depth等于5时需要收割结果）
  2. 终止条件：当startIndex小于len(s)时，需要判断如果深度已经为4且len(s[startIndex:])大于3（即明显会有多余的数字不会被处理），直接返回，从而保证deepth==5时，一定是可以收割结果的；当startIndex不小于len(s)，且depth等于5，此时才将结果添加到res
  3. 单层逻辑：先判断s[start, i+1]是否是合规的数字，如果合规，再将数字添加到path里，再纵向搜索，再弹出以回溯；

131.和本题都是每次将s[start: i+1]子串添加到path里，而最早做的77.组合 以及下面的78.子集每次只用添加一个元素s[i]到path里

另外，这里的深度，可以用len(self.path[:]) == 4 来判断，只要保证只有当self.path长度为4时才能收割结果。

img

回溯代码

  • 时间复杂度: O(3^4)，IP地址最多包含4个数字，每个数字最多有3种可能的分割方式，则搜索树的最大深度为4，每个节点最多有3个子节点。
  • 空间复杂度: O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution:
    # 本题目的递归深度为4
    # 横向遍历的条件，长度从1到3（闭区间）进行遍历（且不能0开始)，剩下的交给纵向
    # 纵向遍历的终止条件，如果最后一次剩下的数字大于3就返回，
    def __init__(self):
        self.res = list()
        self.path = list()

    def isLegal(self, s):
        # 如果开头数字是0，则单独划分，不用继续for循环了
        LofS = len(s)
        if s[0] == '0' and LofS > 1:
            return False
        # 长度大于3，可以不加，传入时已经保证了长度不会大于3
        if LofS > 3:
            return False
        # 大于255
        if int(s) > 255:
            return False
        return True

    def List2IPform(self, s: List):
        return ".".join(s)

    def foo(self, s: str, startIndex: int = 0, depth: int = 1):
        LofS = len(s)
        # 终止条件
        if startIndex < LofS:
          	# 如果最后一次剩下的数字大于3就返回，保证deepth==5时，一定是可以收割结果的
            if depth == 4 and len(s[startIndex:]) > 3:
                return
        else:
            if depth == 5:
                self.res.append(self.List2IPform(self.path[:]))
                return 
        
        # 横向遍历
        for i in range(startIndex, LofS):
            # 如果大于3个长度，直接断
            if i > startIndex + 3:
                break
            # 检测startIndex到i的字符串是否合规
            if self.isLegal(s[startIndex: i + 1]):
              	# 注意这里是一次添加了s[start: i+1]个元素进去
                self.path.append(s[startIndex: i + 1])
                # 剩下的子串交给纵向遍历
                self.foo(s, i + 1, depth + 1)
                self.path.pop()

    def restoreIpAddresses(self, s: str) -> List[str]:
        self.foo(s)
        return self.res

78. 子集

https://leetcode.cn/problems/subsets/

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

1
2
输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

1
2
输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • nums 中的所有元素 互不相同

回溯思路

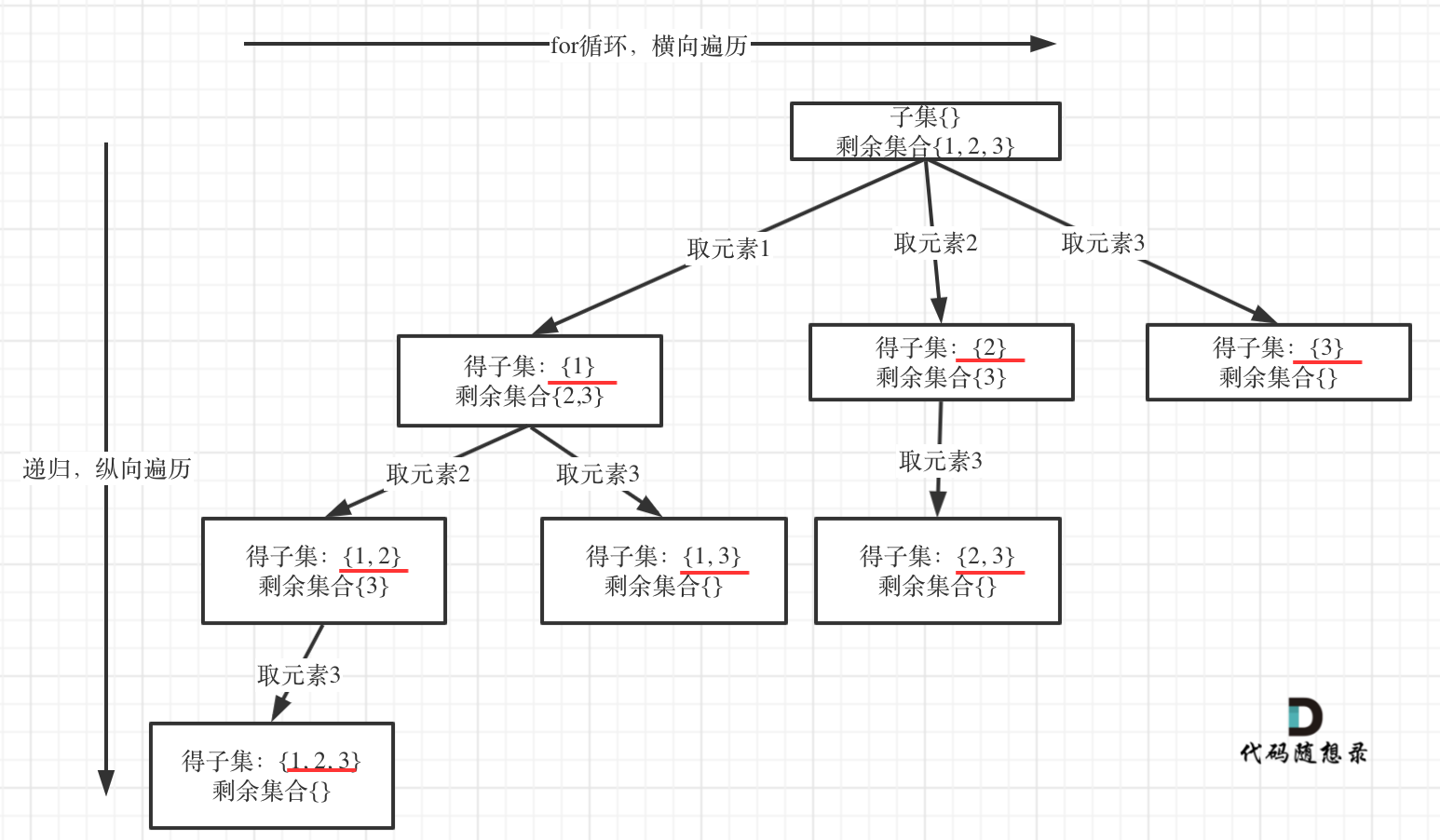
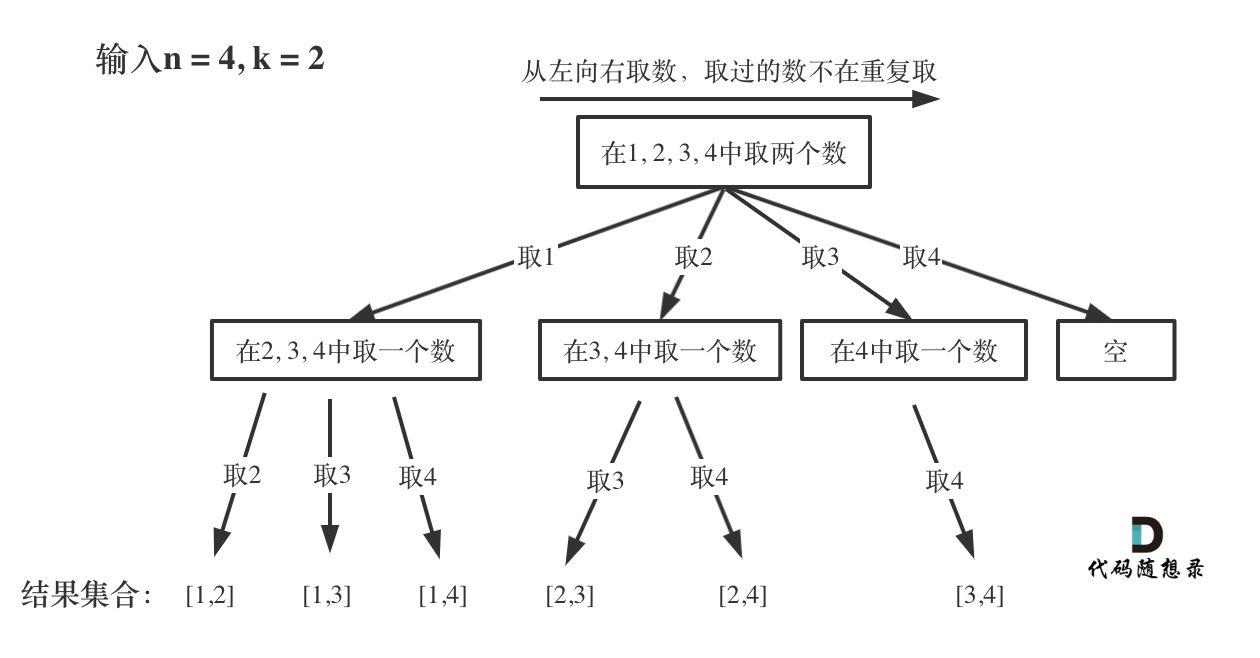
  1. 这题，需要把所有可能的子集都放在res里，本质上是遍历所有可能，在77组合里是求’k’个数的组合，那题目的终止条件（添加到res的条件）是len(path) == k，比如下图所示，只有当path里装了2个时，才将结果放在res；

77组合,k=2的图片

而本题需要将所有遍历结果都装到res，所以它的终止条件（将结果放在res的条件）是空

所以本题的

  1. 输入输出：输入列表和起点下标，无返回值
  2. 终止条件：无
  3. 单层逻辑：添加一个元素s[i]到path里，递归下一层，弹出s[i]以回溯

本题图片

回溯代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def __init__(self):
        self.res = list()
        self.path = list()

    def foo(self, nums: List[int], startIndex: int = 0):
        # 终止条件是空，所有的self.path都能直接丢进去
        self.res.append(self.path[:])
        # 横向遍历
        for i in range(startIndex, LofNums):
          	# 注意，这次只用一次添加一个元素进去
            self.path.append(nums[i])
            # 纵向遍历
            self.foo(nums, i + 1)
            self.path.pop()
        
    def subsets(self, nums: List[int]) -> List[List[int]]:
        self.foo(nums)
        return self.res

90. 子集 II

https://leetcode.cn/problems/subsets-ii/

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的 子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

示例 1：

1
2
输入：nums = [1,2,2]
输出：[[],[1],[1,2],[1,2,2],[2],[2,2]]

示例 2：

1
2
输入：nums = [0]
输出：[[],[0]]

提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10

回溯思路

  1. 这题目和40.组合总和II以及78.子集有点像，不同点是本题需要去重复（去重复的思路和40.组合总和II一样，不过我记得这种需要让nums[i]!=nums[i-1]的思路在之前的题目也遇到过）
  2. 本题和78.子集相比，只添加了这个去重复的约束条件，其它代码一样

回溯代码

  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def __init__(self):
        self.res = list()
        self.path = list()
    
    def foo(self, nums: List[int], startIndex: int = 0):
        self.res.append(self.path[:])
        # print(self.path)
        LofNums = len(nums)
        for i in range(startIndex, LofNums):
            if i > startIndex and nums[i] == nums[i - 1]:
                continue
            self.path.append(nums[i])
            self.foo(nums, i + 1)
            self.path.pop()

    def subsetsWithDup(self, nums: List[int]) -> List[List[int]]:
        nums = sorted(nums)
        self.foo(nums)
        return self.res