LeetCodeCampsDay30贪心part04

三个区间问题的题目，用贪心算法解决

本题需要用到python的lambda表示式

x.sort(key = lambda x: (x[0], x[1]))

表示对列表x进行排序，优先对x[0]从小到大排序，再按x[1]从小到大

如果需要先从大到小，再从小到大，可以先使用-x[0]

x.sort(key = lambda x: (-x[0], x[1]))

452. 用最少数量的箭引爆气球

https://leetcode.cn/problems/minimum-number-of-arrows-to-burst-balloons/

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end， 且满足 xstart ≤ x ≤ x``end，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

示例 1：

1
2
3
4
5
输入：points = [[10,16],[2,8],[1,6],[7,12]]
输出：2
解释：气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

1
2
3
输入：points = [[1,2],[3,4],[5,6],[7,8]]
输出：4
解释：每个气球需要射出一支箭，总共需要4支箭。

示例 3：

1
2
3
4
5
输入：points = [[1,2],[2,3],[3,4],[4,5]]
输出：2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

提示:

  • 1 <= points.length <= 105
  • points[i].length == 2
  • -231 <= xstart < xend <= 231 - 1

贪心思路

本题的最小结果，其实是“最多的重合区间个数”

  1. 对于区间问题，我们先对区间的左端点进行排序（从小到大），如果左端点一样，再按右端点大小到大排序
  2. 随后，再按重复的区间进行讨论（只有两种情况，排序的结果会保证这一点）
    1. 当前区间i左边界大于上一区间(i-1)右边界，即：两个区间无重合，则说明上一个区间i-1需要一个箭
    2. 当前区间i左边界小于等于上一区间i-1右边界，两个区间重合，此时，可以用一个箭射穿两个区间；并且需要更新这两个区间的右边界，让他俩的右边界变成他俩右边界的最小值points[i - 1][1] = points[i][1] = min(points[i - 1][1], points[i][1])；这样做的目的，是为了让下一个区间i+1把当前区间i当成"i-1"进行处理，即，当i-1和i重复了，是否能把i+1也带上一起射穿。

贪心代码

  • 时间复杂度：O(nlog n)，因为有一个快排
  • 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        # 求最多的重合区间个数 = 最小结果
        # 先按左边界对这些区间进行从小到大排序，如果左端点一样，就按右端点从小到大
        points.sort(key = lambda x: (x[0], x[1]))
        # print(points)
        # 再按情况讨论
        # 1、p[i][0] > p[i - 1][1]，当前区间左边界大于上一区间右边界，即：两个区间无重合
        # 2、p[i][0] <= p[i - 1][1]，两个区间重合，此时，可以用一个箭射；并且需要更新这两个区间的右边界，让他俩的右边界变成他俩右边界的最小值
        # 循环，和下一个气球比较
        L = len(points)
        res = 1
        for i in range(1, L):
            if points[i][0] > points[i - 1][1]:
                res += 1
            elif points[i][0] <= points[i - 1][1]:
                # 两个区间的右端点都更新成为两个区间右端点的最小值
                points[i - 1][1] = points[i][1] = min(points[i - 1][1], points[i][1])
        return res

435. 无重叠区间

https://leetcode.cn/problems/non-overlapping-intervals/

给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

注意 只在一点上接触的区间是 不重叠的。例如 [1, 2] 和 [2, 3] 是不重叠的。

示例 1:

1
2
3
输入: intervals = [[1,2],[2,3],[3,4],[1,3]]
输出: 1
解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

1
2
3
输入: intervals = [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

示例 3:

1
2
3
输入: intervals = [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

提示:

  • 1 <= intervals.length <= 105
  • intervals[i].length == 2
  • -5 * 104 <= starti < endi <= 5 * 104

贪心思路

本题和上一题的思路很像，以及代码都非常像；本题是不需要处理不重叠区间的情况；

同样需要注意的一点是，将两个重叠区间的右边界，变成两个区间右端点的最小值，相当于融合成了一个区间，从而让下一个区间和这个新的右端点进行比较判断

贪心代码

  • 时间复杂度：O(nlog n) ，有一个快排
  • 空间复杂度：O(n)，有一个快排，最差情况(倒序)时，需要n次递归调用。因此确实需要O(n)的栈空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int:
        # 本题目就是问有多少个重叠的区间
        # 让相邻的区间保持在一起
        # 先排序区间，再对区间判断
        intervals.sort(key = lambda x: (x[0], x[1]))
        
        L = len(intervals)
        res = 0
        for i in range(1, L):
          	# 如果两个区间重叠
            if intervals[i][0] < intervals[i - 1][1]:
                res += 1
                # 将两个区间的右边界，变成两个区间右端点的最小值
                intervals[i - 1][1] = intervals[i][1] = min(intervals[i - 1][1], intervals[i][1])
        return res

763. 划分字母区间

https://leetcode.cn/problems/partition-labels/

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 "ababcc" 能够被分为 ["abab", "cc"]，但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

1
2
3
4
5
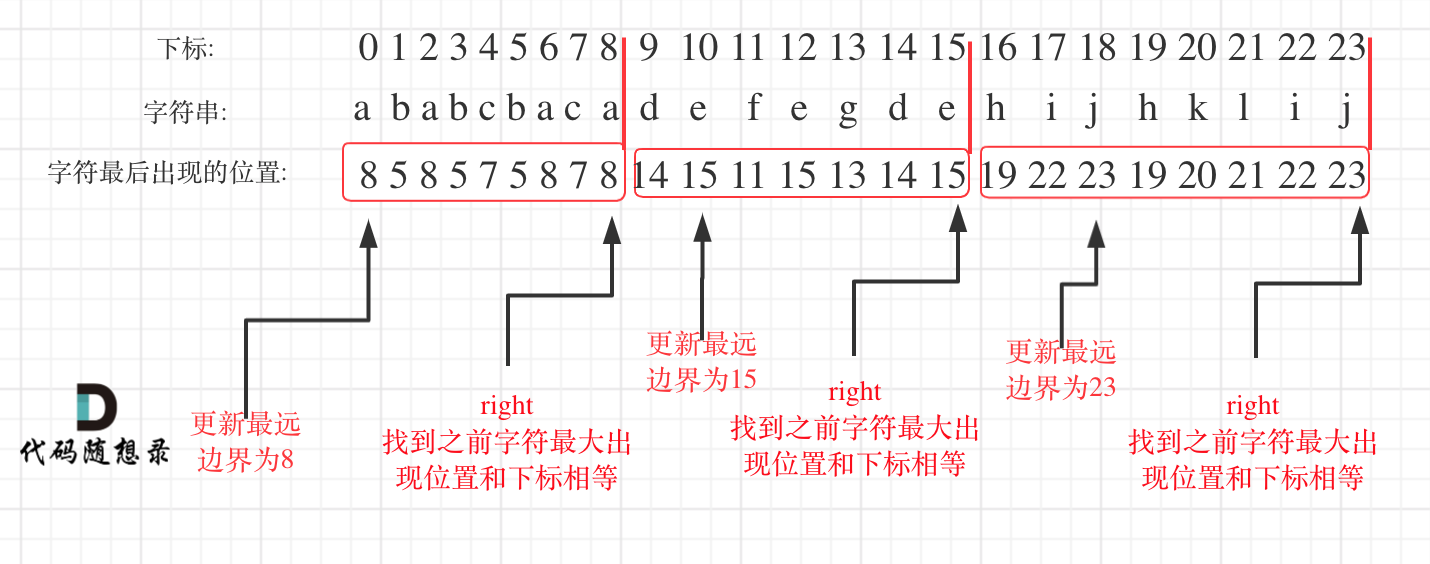
6
输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。

示例 2：

1
2
输入：s = "eccbbbbdec"
输出：[10]

提示：

  • 1 <= s.length <= 500
  • s 仅由小写英文字母组成

贪心思路

思路一：

同一字母最多出现在一个片段中，也暗示这是个区间问题和前面两个题目一样

可以对每个字母看成一个区间（最多有26个区间），记录每个字母的首、末区间位置；然后进行排序，再统计最大重合区间，区间有重合的就合并（按最大右端点合并），并统计合并后区间长度；如果不重叠，则边界就是答案

将区间按左边界从小到大排序，找到边界将区间划分成组，互不重叠。找到的边界就是答案。

思路二：

思路2更灵活，对每个字母来说，使用hashtable，记录每个字母出现的最远位置的下标；（第一次遍历）

再遍历一次，不过这次使用个变量farest，记录当前hashtable里，最远位置的下标，当farest==i时，（比如i=8=farest），此时就达到了一个最长区间。

img

贪心代码

思路一

  • 时间复杂度：O(n)
  • 空间复杂度：O(1)，使用的hash数组是固定大小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution:
    def partitionLabels(self, s: str) -> List[int]:
        # 统计每个字符最后出现的位置，
        # 从头遍历，更新字符的最远出现下标，如果字符最远出现下标与当前下标相等，则找到了分割点
        table = [0] * 26
        L = len(s)
        for i in range(L):
            table[ord(s[i]) - ord('a')] = i

        res = list()
        farest = 0
        start = 0
        for i in range(L):
            farest = max(farest,  table[ord(s[i]) - ord('a')])
            if i == farest:
                res.append(i - start + 1)
                start = i + 1
        return res

思路二代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution:
    def partitionLabels(self, s: str) -> List[int]:
				# 先对s划分成多个区间
        table = dict()
        L = len(s)
        for i in range(L):
            if s[i] not in table:
                table[s[i]] = [i, i]
            else:
                # 更新右端点
                table[s[i]][-1] = i
        # 得到区间后排序
        s_list = list(table.values())
        s_list.sort(key = lambda x: (x[0], x[1]))
				
        L = len(s_list)
        res = list()
        # start用来记录新区间的起点位置，用来计算个数用
        start = 0
        # 开始遍历并查找独立区间、合并重合区间
        for i in range(1, L):
            # 当前区间右端点大于前区间左端点，说明有独立区间
            if s_list[i][0] > s_list[i - 1][1]:
                res.append(s_list[i - 1][1] - start + 1)
                start = s_list[i - 1][1] + 1
            else:
              	# 注意这里是将区间统一变成最大值
                s_list[i][1] = max(s_list[i - 1][1], s_list[i][1])
        res.append(s_list[-1][1] - start + 1)
        return res