LeetCodeCampsDay43动态规划part10
LeetCodeCampsDay43动态规划part10
使用动态规划解决子序列问题
非连续子序列可以看成模板,而连续子序列只是非连续子序列的特例
最长重复子序列需要使用二维dp(每个维度对应一个数组序列)
300. 最长递增子序列
https://leetcode.cn/problems/longest-increasing-subsequence/
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
1 | 输入:nums = [10,9,2,5,3,7,101,18] |
示例 2:
1 | 输入:nums = [0,1,0,3,2,3] |
示例 3:
1 | 输入:nums = [7,7,7,7,7,7,7] |
提示:
1 <= nums.length <= 2500-104 <= nums[i] <= 104
进阶:
- 你能将算法的时间复杂度降低到
O(n log(n))吗?
动态规划思路
本是和139.单词拆分有点儿像,
- dp数组下标与含义:
dp[i]表示第i位置的最长递增子序列长度
- 递推公式
需要有两个指针,一个i指向每个数字;另一个j范围[0~i),包含0不包含i,j指向0到nums[i - 1]之间的数字;
如果nums[i]大于nums[j],则dp[i]可以考虑更新其结果为:dp[i](上一轮的结果)与dp[j]+1中的最大值
dp[i] = max(dp[i], dp[j] + 1)
因为本题目不要求连续,所以可以从 让j从[0~i)(包含0不包含i)中抽数字
- dp初始化
全部初始化为1
- 遍历顺序
先用i遍历数字,再用j遍历[0~i),包含0不包含i
动态规划代码
- 时间复杂度: O(n^2)
- 空间复杂度: O(n)
1 | class Solution: |
674. 最长连续递增序列
https://leetcode.cn/problems/longest-continuous-increasing-subsequence/
给定一个未经排序的整数数组,找到最长且 连续递增的子序列,并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r(l < r)确定,如果对于每个 l <= i < r,都有 nums[i] < nums[i + 1] ,那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
示例 1:
1 | 输入:nums = [1,3,5,4,7] |
示例 2:
1 | 输入:nums = [2,2,2,2,2] |
提示:
1 <= nums.length <= 104-109 <= nums[i] <= 109
动态规划思路
本题目与300.最长递增子序列不同点在于本题要求连续,
- dp数组下标与含义:
dp[i]表示第i位置的最长连续递增子序列长度
- 递推公式
因为本题目要求连续,“连续”意味着在使用j遍历时的起点需要修改成i - 1
需要有两个指针,一个i指向每个数字;另一个j的范围是[i - 1~i),包含i - 1不包含i,j指向0到nums[i - 1]之间的数字;
如果nums[i]大于nums[j],则dp[i]可以考虑更新其结果为:dp[i](上一轮的结果)与dp[j]+1中的最大值
dp[i] = max(dp[i], dp[j] + 1)
或者更直接一点儿
dp[i] = max(dp[i], dp[i - 1] + 1)
- dp初始化
全部初始化为1
- 遍历顺序
先用i遍历数字,再用j遍历[i - 1~i),包含i - 1不包含i
动态规划代码
- 时间复杂度O(N)
- 空间复杂度O(N)
1 | class Solution: |
718. 最长重复子数组
https://leetcode.cn/problems/maximum-length-of-repeated-subarray/
给两个整数数组 nums1 和 nums2 ,返回 两个数组中 公共的 、长度最长的子数组的长度 。
示例 1:
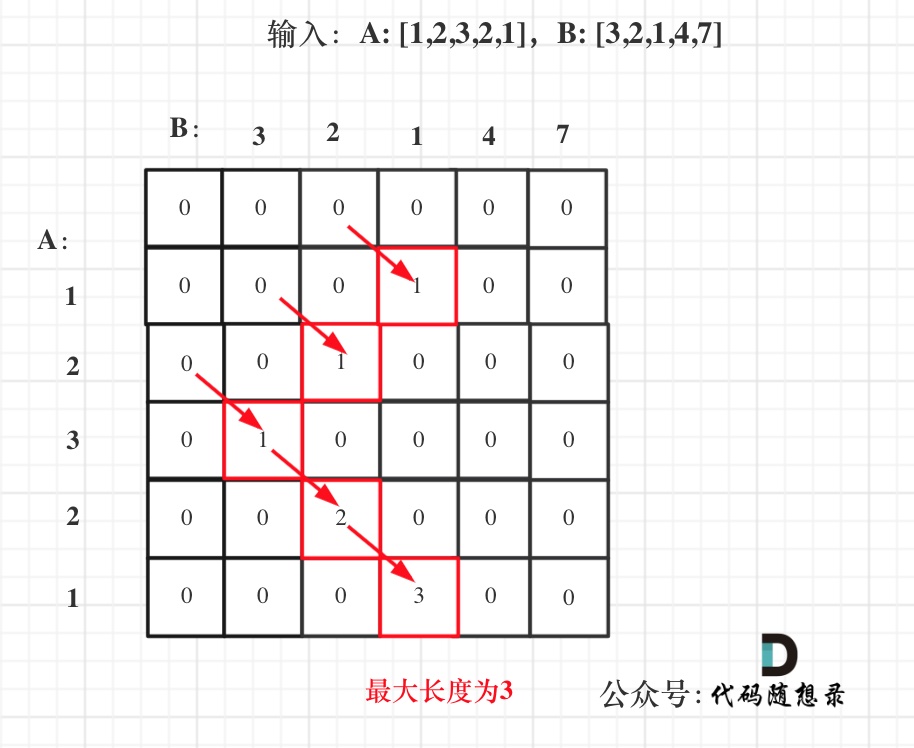
1 | 输入:nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7] |
示例 2:
1 | 输入:nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0] |
提示:
1 <= nums1.length, nums2.length <= 10000 <= nums1[i], nums2[i] <= 100
动态规划思路
- dp下标与定义,
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。
(特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )
- 递推公式
如果nums1[i] == nums2[j],则dp[i][j] = dp[i - 1][j - 1] + 1
如果不相等,则dp[i][j]就是0,因为它打破了连续性
- 初始化
dp[len(nums2) + 1][len(nums1) + 1], dp的必须强行添加一行一列,并且dp[i][0]和dp[0][j]全为0
因为dp[i][j] = dp[i - 1][j - 1]决定了i, j只能从下标1开始
- 遍历顺序
纵向对nums2,横向对nums1;把过来也行,但遍历顺序必须和dp初始化顺序一致
- 举例
以下所有非零值都由其位置的左上角加一得到的
| x | 0 | 1 | 1 | 1 | 1 | |
|---|---|---|---|---|---|---|
| x | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2 | 1 | 1 | 1 |
动态规划代码
- 时间复杂度O(N*M)
- 空间复杂度O(N*M)
1 | class Solution: |