LeetCodeCampsDay44动态规划part11

下面几个子序列的题目都需要使用二维dp，一个维度给text1另一个给text2

并且都需要扩展dp的大小为dp(len(t1)+1, len(t2)+1)，第一行、第一列往往需要填充

所有涉及到两个字符串的dp问题，都有相似的状态转移过程

其中text1[i - 1] == text2[j - 1]，dp[i][j]

以及text1[i - 1] != text2[j - 1]，dp[i][j]

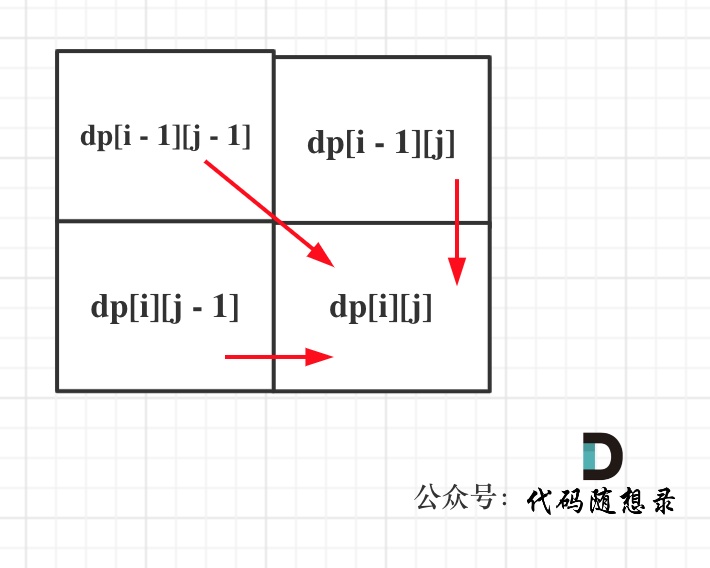
而dp[i][j]只能从dp[i - 1][j - 1]、dp[i - 1][j]、dp[i][j - 1]三种状态转移过来，只要能找到不同条件下状态转移的过程就好解决了

1143. 最长公共子序列

https://leetcode.cn/problems/longest-common-subsequence/

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

1
2
3
输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

1
2
3
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

1
2
3
输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

  • 1 <= text1.length, text2.length <= 1000
  • text1 和 text2 仅由小写英文字符组成。

动态规划思路

  1. dp下标与含义

dp[i][j]表示text1里前i - 1个字符与text2里前j - 1个字符的最长公共子序列长度

  1. 递推公式

可以看出来，有三个方向可以转移到dp[i][j]

img

img

如果text2[i - 1] == text1[j - 1], 则dp[i][j] = dp[i - 1][j - 1] + 1

如果不相等, 则dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])

假如t1 = “ezupkr”，t2 = “ubmrapg”，我们仅看前几个字符，当前的dp数组如下

None e z u
None 0 0 0 0
u 0 0 0 1
b 0 0 0 1

当两个字符相等时：dp[1][3] = dp[0][2] + 1 = 0 + 1 = 1，我们此时只用关心在t1里"u"和t2里的"u"，把这两个子串看成一个新的题目，新题目的dp’数组如下

None u
None 0 0
u 0 1

dp’[1][1]对应新题目里的u位置，dp’[1][1]=dp’[0][0]+1，不用管dp’[0][0]对应的字符是什么；

当两个字符不相等时：比如t1=b, t2=u时，dp[2][3] = max(dp[2][2], dp[1][3])

​ dp[2][2]的情况可以理解成把t1=ez, t2=ub，求这新题目的最大序列数

​ dp[1][3]的情况可以理解成把t1=ezu, t2=u，求这新题目的最大序列数

dp[2][3]此时相等于求“t1=ez, t2=ub”和“t1=ezu, t2=u”这两种情况的最大值

  1. 遍历顺序

纵向遍历t2，横向遍历t1，反之也行

  1. 初始化

dp[len(t1) + 1][len(t2) + 1]，并且全部初始化为0

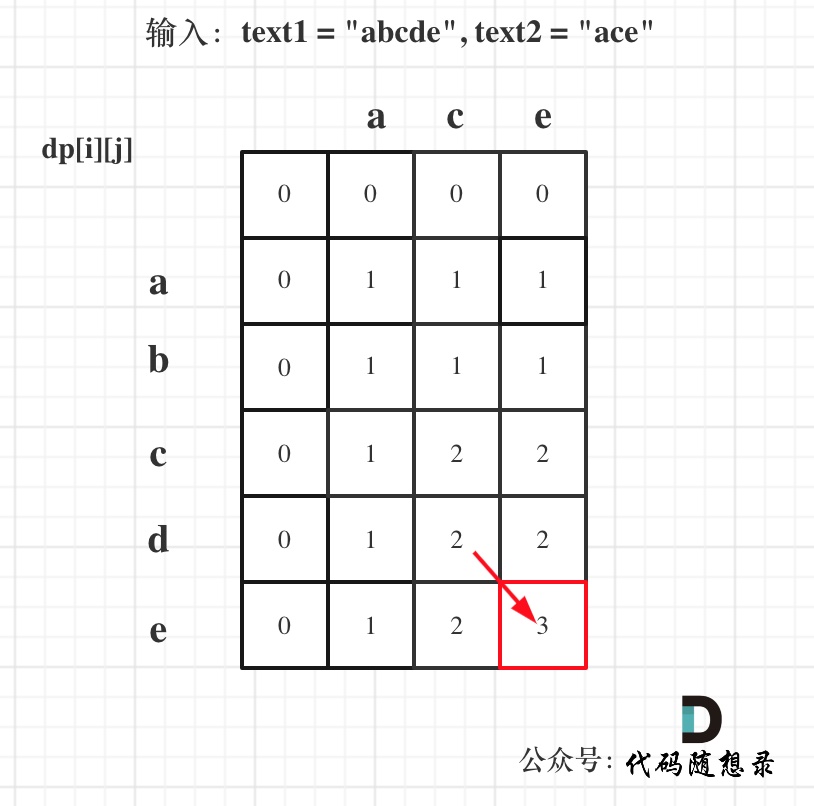
  1. 举例

以输入：text1 = “abcde”, text2 = “ace” 为例，dp状态如图：

1143.最长公共子序列1

1143.最长公共子序列1

本题目还有个特性：不能交叉，

举例t1 = abcde, t2 = ec，最终结果应该是1而不是2，即必须按顺序来；如果t1里的c和t2里的c对应了，再让t1里的e和t2里的e对应，就出来了交叉（和1035. 不相交的钱是相似的思路）

None e c
None 0 0 0
a 0 0 0
b 0 0 0
c 0 0 1
d 0 0 1
e 0 1 1

动态规划代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution:
    def longestCommonSubsequence(self, text1: str, text2: str) -> int:
        # 本题可能和139.单词拆分、300. 最长递增子序列 有点儿像，
        
        # dp下标与含义：dp[i][j]表示text1里前i - 1个字符与text2里前j - 1个字符的最长公共子序列长度
        # 因为dp的第一行第一列会被填写为0

        # 递推公式
        # 如果text2[i - 1] == text1[j - 1]
        # 则dp[i][j] = dp[i - 1][j - 1] + 1
        # 如果不相等
        # 则dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])

        # 遍历顺序
        # 纵向遍历t2，横向遍历t1，反之也行

        L1 = len(text1)
        L2 = len(text2)

        dp = [[0] * (L1 + 1) for _ in range(L2 + 1)]

        res = 0
        for i in range(1, L2 + 1):
            for j in range(1, L1 + 1):
                if text2[i - 1] == text1[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    # 注意这个取值需要同时取两者最大

                    # 比如t1 = "ezupkr"，t2 = "ubmrapg"时包含令dp[i][j] = dp[i - 1][j]的情况
                    # 而t1 = "abcde"， t2 = "ace"包含令dp[i][j] = dp[i][j - 1]的情况
                    dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])
            res = max(res, dp[i][j])
        
        return res

1035. 不相交的线

https://leetcode.cn/problems/uncrossed-lines/

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足：

  • nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

示例 1：

img

1
2
3
4
输入：nums1 = [1,4,2], nums2 = [1,2,4]
输出：2
解释：可以画出两条不交叉的线，如上图所示。 
但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

示例 2：

1
2
输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2]
输出：3

示例 3：

1
2
输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1]
输出：2

提示：

  • 1 <= nums1.length, nums2.length <= 500
  • 1 <= nums1[i], nums2[j] <= 2000

动态规划思路

这题目和1143.最长公共子序列 代码完全一样，解决思路也是一样的；

这里说直线无法交叉也是1143.最长公共子序列 拥有的性质，说明在字符串text1中 找到一个与字符串text2相同的子序列，且这个子序列不能改变相对顺序

举例t1 = abcde, t2 = ec，最终结果应该是1而不是2，因为公共子序列必须按顺序来；

如果t1里的c和t2里的c对应了，再让t1里的e和t2里的e对应，就出来了交叉

None e c
None 0 0 0
a 0 0 0
b 0 0 0
c 0 0 1
d 0 0 1
e 0 1 1

回到本题目，直线不能相交，这就是说明在字符串nums1中 找到一个与字符串nums2相同的子序列，且这个子序列不能改变相对顺序，只要相对顺序不改变，连接相同数字的直线就不会相交。

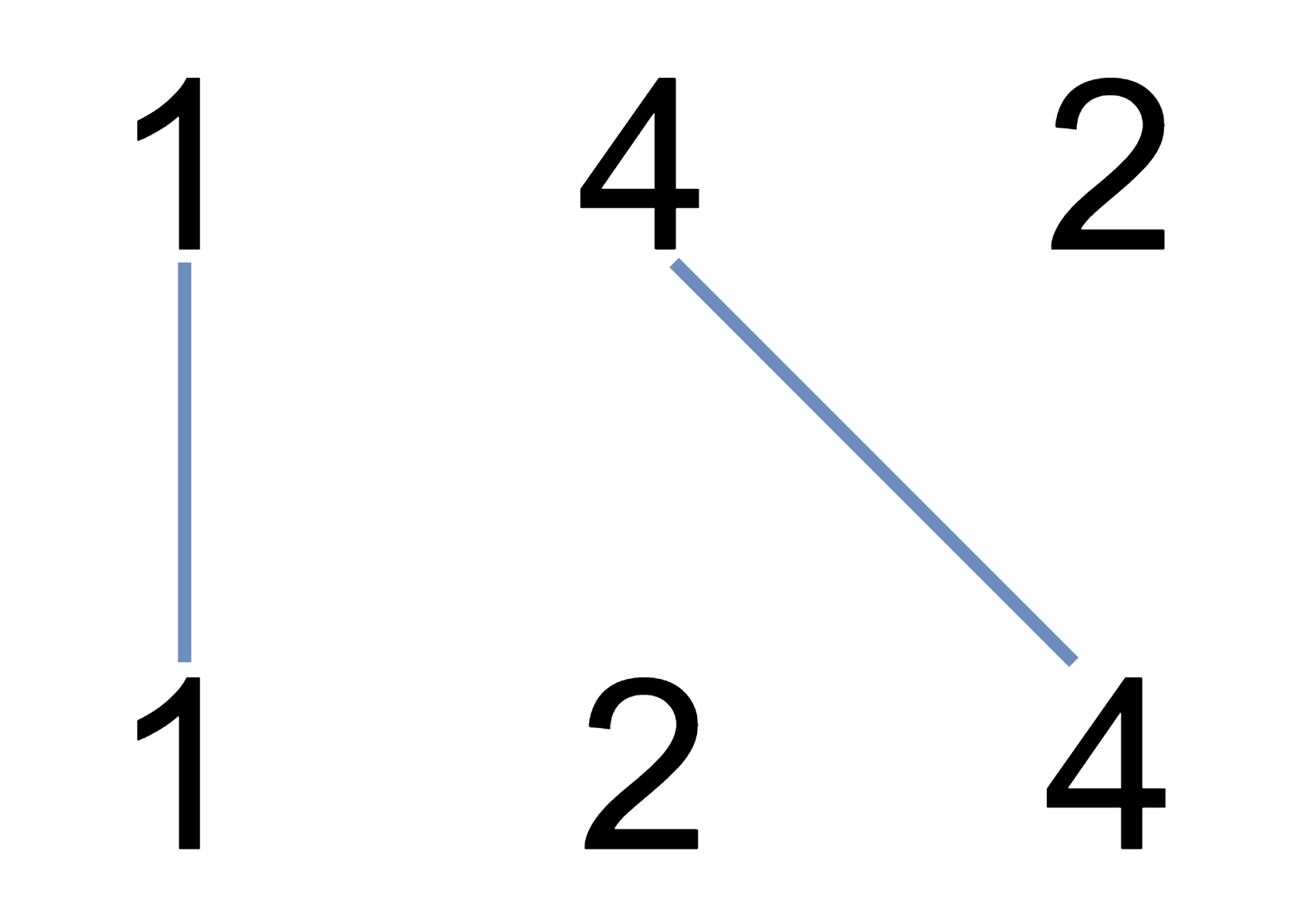
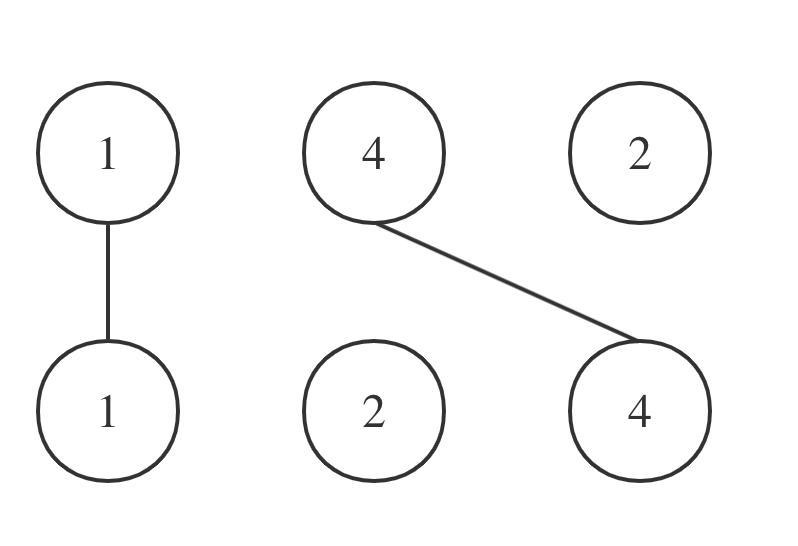
拿示例一nums1 = [1,4,2], nums2 = [1,2,4]为例，相交情况如图：

img

img

其实也就是说nums1和nums2的最长公共子序列是[1,4]，长度为2。 这个公共子序列指的是相对顺序不变（即数字4在字符串nums1中数字1的后面，那么数字4也应该在字符串nums2数字1的后面）

这么分析完之后，大家可以发现：本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

  1. dp下标与含义

dp[i][j]表示nums1[i - 1]与nums2[j - 1]最多的不相交线数（按顺序的公共子序列数）

  1. 递推公式

可以看出来，有三个方向可以转移到dp[i][j]

img

img

如果text2[i - 1] == text1[j - 1], 则dp[i][j] = dp[i - 1][j - 1] + 1

如果不相等, 则dp[i][j] = max(dp[i][j - 1], dp[i - 1][j])

  1. 初始化

dp[len(nums1) + 1][len(nusm2) + 1]，并且全部初始化为0

  1. 遍历顺序

纵向遍历t1，横向遍历t2，反之也行

动态规划代码

  • 时间复杂度O(N*M)
  • 空间复杂度O(N*M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:
        # 本题和1143最长公共子序列是一样的思路，代码也基础一样
        # 在

        L1 = len(nums1)
        L2 = len(nums2)

        dp = [[0] * (L2 + 1) for _ in range(L1 + 1)]

        res = 0
        for i in range(1, L1 + 1):
            for j in range(1, L2 + 1):
                if nums1[i - 1] == nums2[j - 1]:
                    dp[i][j] = dp[i - 1][j - 1] + 1
                else:
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
            res = max(res, dp[i][j])

        return res

53. 最大子数组和

https://leetcode.cn/problems/maximum-subarray/

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

1
2
3
输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

1
2
输入：nums = [1]
输出：1

示例 3：

1
2
输入：nums = [5,4,-1,7,8]
输出：23

提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

动态规划思路

使用一维数组

  1. dp下标与含义：

dp[i][0]表示拿第i个数字的最大和，dp[i][1]表示不拿第i个数字的最大和

  1. 递推公式

如果拿第i个数字 dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]) + nums[i]

如果不拿第i个数字 dp[i][1] = 0 （因为本题要求连续子数组，如果不要求连续，dp[i][1] = max(dp[i - 1][0], dp[i - 1][1])）

  1. 初始化

dp = [[0] * 2 for _ in range(len(nums) + 1)]

并且全部初始化为0

  1. 遍历顺序

纵向nums， 横向只有0/1两个状态

其实和贪心算法的思路也是相似的，因为dp[i - 1][1]恒定为0，每次在拿时会判断：如果当前dp[i - 1][0]小于0，则直接取0，再加上nums[i]

动态规划代码

  • 时间复杂度O(N)
  • 空间复杂度O(N)
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        L = len(nums)
        dp = [[0] * 2 for _ in range(L + 1)]

        res = nums[0]
        for i in range(1, L + 1):
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1]) + nums[i - 1]
            dp[i][1] = 0 # 可以不写
            res = max(res, dp[i][0])
        
        return res

由于dp[i][1]恒定为0，所以dp也可以仅用一个状态

优化后代码

1
2
3
4
5
6
7
8
9
10
11
class Solution:
    def maxSubArray(self, nums: List[int]) -> int:
        L = len(nums)
        dp = [0] * (L + 1)

        res = nums[0]
        for i in range(1, L + 1):
            dp[i] = max(dp[i - 1], 0) + nums[i - 1]
            res = max(res, dp[i])
        
        return res

392. 判断子序列

https://leetcode.cn/problems/is-subsequence/

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

致谢：

特别感谢 @pbrother 添加此问题并且创建所有测试用例。

示例 1：

1
2
输入：s = "abc", t = "ahbgdc"
输出：true

示例 2：

1
2
输入：s = "axc", t = "ahbgdc"
输出：false

提示：

  • 0 <= s.length <= 100
  • 0 <= t.length <= 10^4
  • 两个字符串都只由小写字符组成。

动态规划思路

  1. dp下标与定义

dp[i][j]表示s里前s[j - 1]字符是t[i - 1]的子序列，dp[i][j]只为T/F

  1. 递推公式

如果t[i - 1] == s[j - 1]并且dp[i - 1][j - 1]为True，则dp[i][j]=True

否则dp[i][j] = dp[i - 1][j]

  1. 初始化

dp = [[False] * (Ls + 1) for _ in range(Lt + 1)]

由递推公式知，我们需要一行、一列空表示空字符串

但让第一列为True，表示如果s=None时一定是t的子序列

  1. 遍历顺序

纵向遍历t，横向遍历s

  1. 举例，

s = abc, t = ahbgdc

​ None a b c

None T F F F

a T T F F

h T T F F

b T T T F

g T T T F

d T T T F

c T T T T

动态规划代码

  • 时间复杂度O(N * M)
  • 空间复杂度O(N * M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def isSubsequence(self, s: str, t: str) -> bool:
        Ls = len(s)
        Lt = len(t)
        dp = [[False] * (Ls + 1) for _ in range(Lt + 1)]
        # 第一列初始化为True
        for i in range(Lt + 1):
            dp[i][0] = True

        for i in range(1, Lt + 1):
            for j in range(1, Ls + 1):
                if s[j - 1] == t[i - 1] and dp[i - 1][j - 1] is True:
                    dp[i][j] = True
                else:
                    # 
                    dp[i][j] = dp[i - 1][j]

        return dp[-1][-1]