LeetCodeCampsDay46动态规划part13

使用dp解决回文串和回文序列问题

647. 回文子串

https://leetcode.cn/problems/palindromic-substrings/

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

回文字符串 是正着读和倒过来读一样的字符串。

子字符串 是字符串中的由连续字符组成的一个序列。

示例 1：

1
2
3
输入：s = "abc"
输出：3
解释：三个回文子串: "a", "b", "c"

示例 2：

1
2
3
输入：s = "aaa"
输出：6
解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

提示：

  • 1 <= s.length <= 1000
  • s 由小写英文字母组成

普通思路

本题和前面写过的26. 单词拆分有点像

需要将s拆分成长度为1、2、…L的子串，做法：使用双指针，i作为子串结尾位置；j作为子串起点位置，从而对所有子串进行判断是否为回文串；

比如s= ‘abc’，将得到a, ab, b, abc, bc, c 再对每个子串判断是否为回文串（调用个函数即可）

但这种写法会超时，因为有太多的重复内容被反复计算

所以需要有dp的方法来判断回文串

普通代码（超时）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution:
    def countSubstrings(self, s: str) -> int:
        def isLegal(s: str) -> bool:
            left = 0
            right = len(s) - 1
            while left < right:
                if s[left] != s[right]:
                    return False
                left += 1
                right -= 1
            return True
        
        L = len(s)
        res = 0
        for i in range(1, L + 1):
            for j in range(i):
                # print(s[j: i])
                if isLegal(s[j: i]):
                    res += 1
        
        return res

动态规划思路

一个更好的思路，把问题拆成子问题

比如为了判断abcba是否为子串，可以先判断bcb是否为子串->判断c是否为子串

所以问题可以变成

img

img

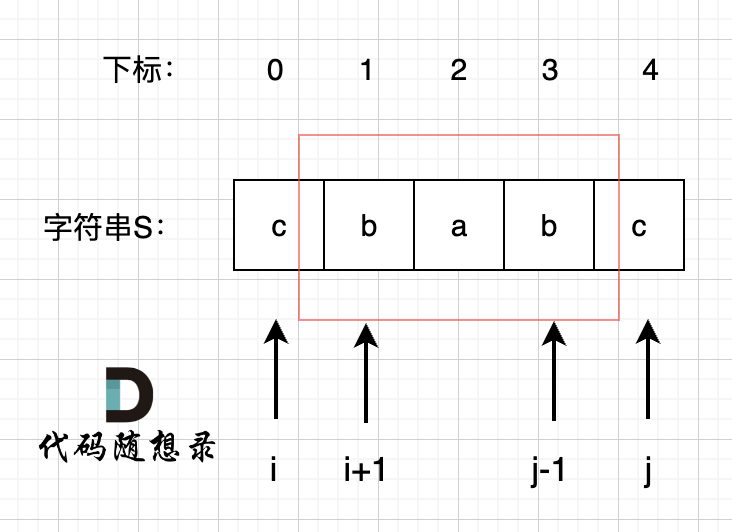
同时使用两个指针遍历，和普通思路一样，也需要将s拆分成长度为1、2、…L的子串s[j: i]（左闭右闭）

  • 如果长度为1，即s[j]==s[i]且j==i，那一定是回文，令dp[j][i]=1
  • 如果长度为2，即s[j]==s[i]且j+1==i，也是回文，令dp[j][i]=1
  • 如果长度大于2，比如abcba，即s[j]==s[i]=a，且j+1<i，此时需要判断s[j+1:i-1]（左闭右闭）这一段(bcb)是否为回文串，如果bcb已经是回文串（即令dp[j + 1][i - 1]=1），那s[j:i]（左闭右闭），也是回文，令dp[j][i]=1；否则就不是回文

反之

  • 如果s[j]!=s[i]，那一定不是回文串

动态规划代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def countSubstrings(self, s: str) -> int:
        # 下面使用动态规划解决
        L = len(s)
        res = 0
        dp = [[False] * (L + 1) for _ in range(L + 1)]
        # 全部初始化为False即可

        for i in range(1, L + 1):
            for j in range(1, i + 1):
                # print(s[j - 1], s[i - 1])
                if s[j - 1] == s[i - 1]:
                    if j == i:
                        # 同一个字符且位置相同
                        res += 1
                        dp[j][i] = True    
                    elif j + 1 == i:
                        # 相邻两个字符
                        res += 1
                        dp[j][i] = True    
                    else:
                        # j与i之间有其它字符，此时要判断s[j+1: i-1]（左闭右闭）是否为回文，如果它也是回文，才能说明s[j: i]（左闭右闭）是回文
                        if dp[j + 1][i - 1]:
                            dp[j][i] = True 
                            res += 1                   
        # print(dp)
        return res

注意这里的遍历顺序，最好是i从后向前遍历，因为在状态转换时需要使用dp[i + 1][j - 1]

所以i的范围从[L-1, 0]而j的范围从[i, L-1]，而dp的含义还是s[j-1,i+1]这段字符串是否为回文

代码改进

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# 下面使用动态规划解决
L = len(s)
res = 0
dp = [[False] * (L) for _ in range(L)]
# 全部初始化为False即可

for i in range(L - 1, -1, -1):
    for j in range(i, L):
        # print(s[j - 1], s[i - 1])
        if s[j] == s[i]:
            if j == i:
                # 同一个字符且位置相同
                res += 1
                dp[i][j] = True    
            elif j - 1 == i:
                # 相邻两个字符
                res += 1
                dp[i][j] = True    
            else:
                # j与i之间有其它字符，此时要判断s[j+1: i-1]（左闭右闭）是否为回文，如果它也是回文，才能说明s[j: i]（左闭右闭）是回文
                if dp[i + 1][j - 1]:
                    dp[i][j] = True 
                    res += 1                   
# print(dp)
return res

516. 最长回文子序列

https://leetcode.cn/problems/longest-palindromic-subsequence/

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

示例 1：

1
2
3
输入：s = "bbbab"
输出：4
解释：一个可能的最长回文子序列为 "bbbb" 。

示例 2：

1
2
3
输入：s = "cbbd"
输出：2
解释：一个可能的最长回文子序列为 "bb" 。

提示：

  • 1 <= s.length <= 1000
  • s 仅由小写英文字母组成

动态规划思路

注意这题是回文子序列（不要求连续）

仍然可以使用dp数组做，和647. 回文子串思路相似

  1. dp下标与含义

dp[i][j]表示s[i:j]（左闭右闭）的最长的回文子序列长度

  1. 递推公式

在判断回文子串的题目中，关键逻辑就是看s[i]与s[j]是否相同。

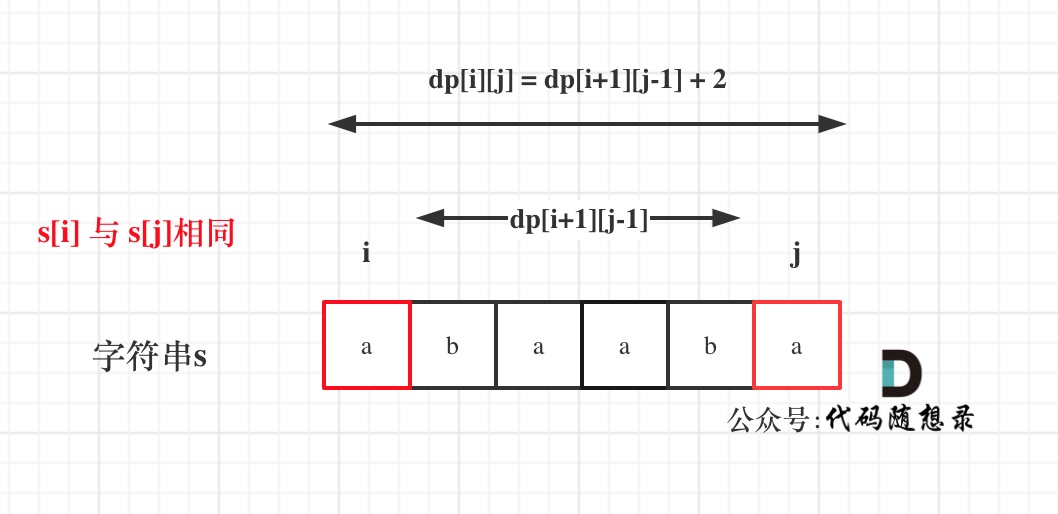
如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2

如图：

516.最长回文子序列

516.最长回文子序列

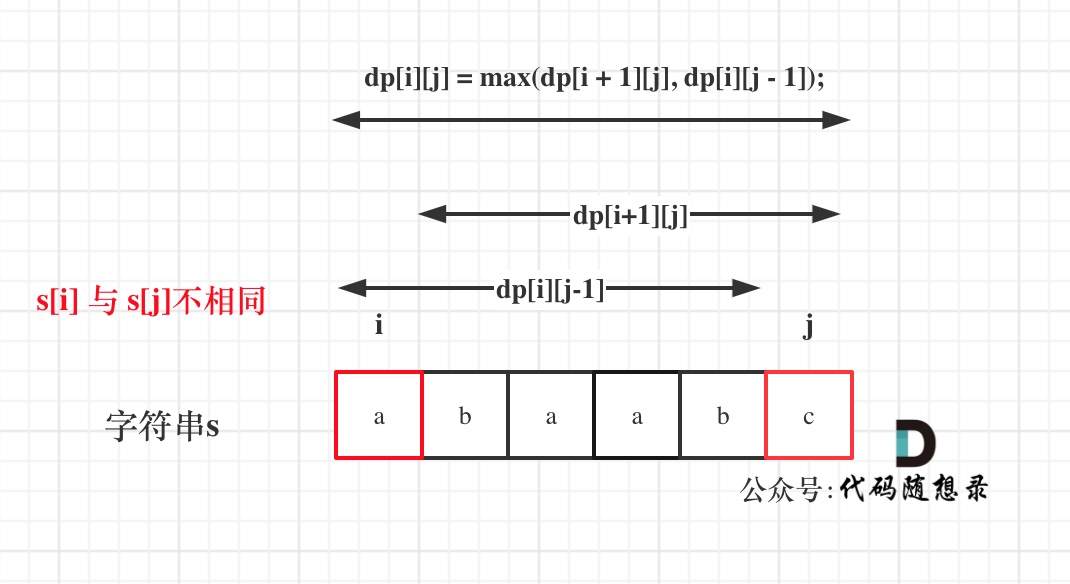
如果不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子序列的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。

加入s[j]的回文子序列长度为dp[i + 1][j]。

加入s[i]的回文子序列长度为dp[i][j - 1]。

那么dp[i][j]一定是取最大的，即：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

516.最长回文子序列1

516.最长回文子序列1

  1. 初始化

首先要考虑当i 和j 相同的情况，从递推公式：dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出 递推公式是计算不到 i 和j相同时候的情况。

所以需要手动的将i==j的情况全部初始化为1，其它值初始化为0

当然，也可以不手动初始化，但需要在s[i]==s[j]时，手动添加判断条件，如果i==j则赋值为1；而且j - 1==i时需要手动赋值为2

  1. 遍历顺序

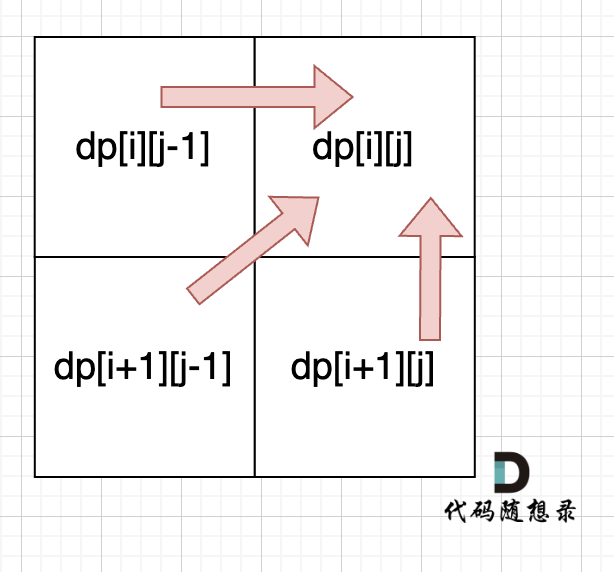
从递归公式中，可以看出，dp[i][j] 依赖于 dp[i + 1][j - 1] ，dp[i + 1][j] 和 dp[i][j - 1]，如图：

img

img

所以遍历i的时候一定要从下到上遍历，这样才能保证下一行的数据是经过计算的。

动态规划代码

  • 时间复杂度O(N^2)
  • 空间复杂度O(N^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # dp下标与含义
        # dp[i][j]表示s[j:i]（左闭右闭）的最长回文子序列

        L = len(s)
        dp = [[0] * L for _ in range(L)]


        for i in range(L - 1, -1, -1):
            for j in range(i, L):
                if s[i] == s[j]:
                    if i == j:
                        dp[i][j] = 1
                    elif j - 1 == i:
                        dp[i][j] = 2
                    elif dp[i + 1][j - 1] != 0:
                        dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i][j - 1], dp[i + 1][j])

        return dp[0][-1]

动态规划代码二

手动初始化

  • 时间复杂度O(N^2)
  • 空间复杂度O(N^2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution:
    def longestPalindromeSubseq(self, s: str) -> int:
        # dp下标与含义
        # dp[i][j]表示s[j:i]（左闭右闭）的最长回文子序列

        L = len(s)
        dp = [[0] * L for _ in range(L)]

        # 对角线全为1
        for i in range(L):
            dp[i][i] = 1
            
        for i in range(L - 1, -1, -1):
            for j in range(i + 1, L):
                if s[i] == s[j]:
                    dp[i][j] = dp[i + 1][j - 1] + 2
                else:
                    dp[i][j] = max(dp[i][j - 1], dp[i + 1][j])

        return dp[0][-1]