LeetCodeCampsDay60图论part10

94.城市间货物运输 I

https://kamacoder.com/problempage.php?pid=1152

题目描述

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。如果最低运输成本是一个负数，它表示在遵循最优路径的情况下，运输过程中反而能够实现盈利。

城市 1 到城市 n 之间可能会出现没有路径的情况，同时保证道路网络中不存在任何负权回路。

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v （单向图）。

输出描述

如果能够从城市 1 到连通到城市 n， 请输出一个整数，表示运输成本。如果该整数是负数，则表示实现了盈利。如果从城市 1 没有路径可达城市 n，请输出 “unconnected”。

输入示例

1
2
3
4
5
6
7
8
6 7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5

输出示例

1
1

提示信息

img

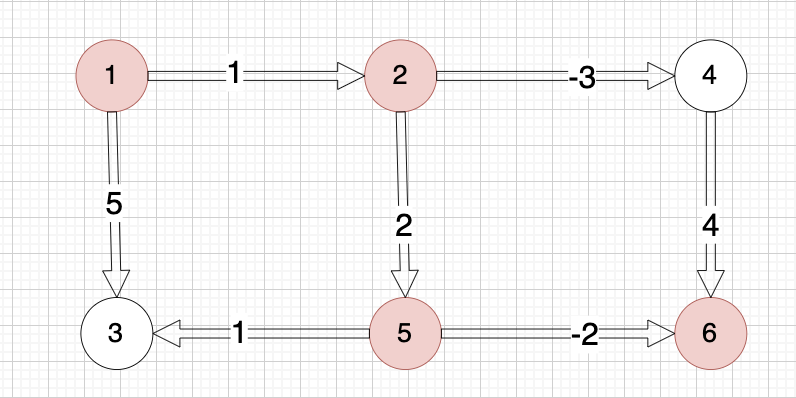
示例中最佳路径是从 1 -> 2 -> 5 -> 6，路上的权值分别为 1 2 -2，最终的最低运输成本为 1 + 2 + (-2) = 1。

示例 2：

4 2
1 2 -1
3 4 -1

在此示例中，无法找到一条路径从 1 通往 4，所以此时应该输出 “unconnected”。

数据范围：

1 <= n <= 1000；
1 <= m <= 10000;

-100 <= v <= 100;

Bellman-ford优化思路

观察之前的代码，可以发现在遍历阶段可以优化，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def main():
    n, m = map(int, input().split())
    graph = list()

    for _ in range(m):
        s, t, v = map(int, input().split())
        graph.append([s, t, v])

    minDist = [float('inf')] * (n + 1)
    minDist[1] = 0

    for i in range(1, n):
        updated = False
        for edge in graph:
            s, t, v = edge
            if minDist[s] != float('inf') and minDist[s] + v < minDist[t]:
                minDist[t] = minDist[s] + v
                # 添加个updated防止死循环，比如一直找不到满足条件的源点时
                updated = True
        if not updated:
            break
    
    print(minDist[-1] if minDist[-1] != float('inf') else "unconnected")

if __name__ == "__main__":
    main()

原代码的遍历条件是需要遍历(n-1)次，并且每次都要对整个graph遍历，虽然使用了minDist[s] != float(‘inf’)和minDist[s] + v < minDist[t]这个条件来筛选更新对象，这样的思路虽然简单（可能也不简单？），但增加了很多无效遍历

输入的边为以下

1
2
3
4
5
6
7
5 6 -2
1 2 1
5 3 1
2 5 2
2 4 -3
4 6 4
1 3 5

比如刚开始minDist[1]=0，

  1. edge信息为(s=5, t=6, v=-2)，此时minDist[s]为正无穷，不是要找的源点
  2. edge信息为(s=1, t=2, v=1)，此时minDist[s]为0，说明找到了源点 ，再进行“relax”，即对经过源点（1）能到达的终点（2）进行路径距离更新，如果minDist[s] + v < minDist[t] ，说明经过源点s再到终点t是距离更近的
  3. edge信息为(s=5, t=3, v=1)，此时minDist[s]为正无穷，不是要找的源点
  4. …
  5. edge信息为(s=1, t=3, v=5)，此时minDist[s]为0，说明找到了源点 ，再更新终点（3）的距离

这仅是一轮遍历，可以发现这么一次搜索，仅有找到了两次源点，而其它的都是无效的

此外，假如minDist[1]=0已经更新完成，此时i=2，即源点=2

  1. edge信息为(s=5, t=6, v=-2)，此时minDist[s]为正无穷，不是要找的源点
  2. edge信息为(s=1, t=2, v=1)，此时minDist[s]不为正无穷，但**minDist[s] + v < minDist[t]**已经不满足条件了，因为minDist[2]已经等于minDist[1] + 1，不是要找的源点
  3. edge信息为(s=5, t=3, v=1)，此时minDist[s]为正无穷，不是要找的源点
  4. edge信息为(s=2, t=5, v=2)，此时minDist[s]为0，说明找到了源点，再进行“relax”，即对经过源点（2）能到达的终点（5）进行路径距离更新
  5. …

这仅是一轮遍历，可以发现这么一次搜索，仅有找到了两次源点，而其它的都是无效的

和dijkstra优化思路相似，可以使用一个邻接表+队列来控制哪些元素需要被遍历，从而减少无效遍历

graph需要使用邻接表，其中s作为下标索引，而存储的是 <t, v> 这个结构体列表

1
2
3
4
5
6
7
8
9
class Edge:
    def __init__(self, t, v):
        self.t = t
        self.v = v

graph = [[] for _ in range(n + 1)]
for _ in range(m):
    s, t, v = map(int, input().split())
    graph[s].append(Edge(t, v))

比如，输入的边会变成下面这样的邻接表

1
2
3
4
1 [<2, 1>, <3, 5>]
2 [<5, 2>, <4, -3>]
4 [<6, 4>]
5 [<6, -2>, <3, 1>]

先将起点1添加到que中，若que不为空则一直弹出元素s，并对graph[s]遍历，注意graph[s]是个列表，里面是与它相连的终点

更新到每个终点的距离

这里还有个优化过程，如果某个终点已经达到过了，则不让它反复添加到队列里，设置个inQue即可

1
2
inQue = [False] * (n + 1)
inQue[1] = True

简单来说，如果不添加inQue之所以在某些情况下能通过，是因为那些测试用的图不包含负权回路。但是，这个代码存在一个致命缺陷：一旦图中存在负权回路，它就会陷入无限循环。

所以，在后面95题目中，因为有负权回路，它必须要添加个inQue来判断

详细解释

在一个没有负权回路的图中（无论边权是正还是负），一个节点的最短路径值 minDist 虽然可能会被更新多次，但更新的次数是有限的。

想象一下，从起点到节点 X 的最短路径值为 10。后来你又找到一条路径，值为 8，于是你更新 minDist[X] 并将 X 放入队列。再后来，你又找到一条更短的路径，值为 5，你再次更新并放入队列。

因为没有负权回路，节点的 minDist 值会一直降低，但它有一个最终的、最低的“底线”。一旦所有节点的 minDist 都达到了这个底线值，就不会再有新的更新了 (if 条件不再满足)，队列最终会变空，程序正常结束。

所以，对于有向无环图 (DAG) 或者没有负权回路的图，你的代码可以算出正确答案，只是效率可能不高。

Bellman-ford优化代码

队列优化版Bellman_ford 的时间复杂度 并不稳定，效率高低依赖于图的结构。

例如 如果是一个双向图，且每一个节点和所有其他节点都相连的话，那么该算法的时间复杂度就接近于 Bellman_ford 的 O(N * E) N 为节点数量，E为边的数量。

在这种图中，每一个节点都会重复加入队列 n - 1次，因为 这种图中 每个节点 都有 n-1 条指向该节点的边，每条边指向该节点，就需要加入一次队列。（如果这里看不懂，可以在重温一下代码逻辑）

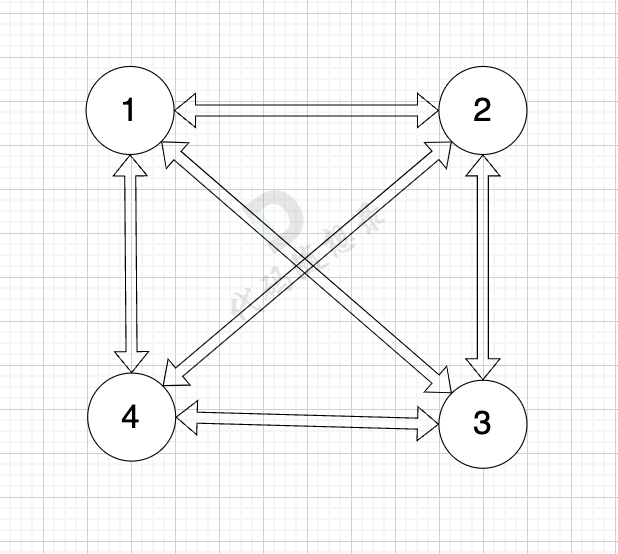
至于为什么 双向图且每一个节点和所有其他节点都相连的话，每个节点 都有 n-1 条指向该节点的边， 我再来举个例子，如图：

img

img

图中 每个节点都与其他所有节点相连，节点数n 为 4，每个节点都有3条指向该节点的边，即入度为3。

n为其他数值的时候，也是一样的。

当然这种图是比较极端的情况，也是最稠密的图。

所以如果图越稠密，则 SPFA的效率越接近与 Bellman_ford。

反之，图越稀疏，SPFA的效率就越高。

一般来说，SPFA 的时间复杂度为 O(K * N) K 为不定值，因为 节点需要计入几次队列取决于 图的稠密度。

如果图是一条线形图且单向的话，每个节点的入度为1，那么只需要加入一次队列，这样时间复杂度就是 O(N)。

所以 SPFA 在最坏的情况下是 O(N * E)，但 一般情况下 时间复杂度为 O(K * N)。

尽管如此，以上分析都是 理论上的时间复杂度分析。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Edge:
    def __init__(self, t, v):
        self.t = t
        self.v = v


def main():
    n, m = map(int, input().split())
    graph = [[] for _ in range(n + 1)]

    for _ in range(m):
        s, t, v = map(int, input().split())
        graph[s].append(Edge(t, v))

    minDist = [float('inf')] * (n + 1)
    minDist[1] = 0

    from collections import deque
    que = deque()
    que.append(1)
    # 这个inQue不添加似乎也可，但必须要保证没有负权回路，如果有负权回路，必须要添加inQue
    # 使用一个布尔数组 inQue 来在 O(1) 时间内完成判断
    inQue = [False] * (n + 1)
    inQue[1] = True

    while que:
        s = que.popleft()
        # 从队列里取出的时候，要取消标记，我们只保证已经在队列里的元素不用重复加入
        # 把节点 s 标记为“当前不在队列中”，以便它将来如果被再次更新，还有机会重新加入队列
        inQue[s] = False 
        for edge in graph[s]:
            t, v = edge.t, edge.v
            if minDist[s] + v < minDist[t]:
                minDist[t] = minDist[s] + v
                # 已经在队列里的元素不用重复添加
                if inQue[t] == False:
                    que.append(t)
                    inQue[t] = True
            
    print(minDist[-1] if minDist[-1] != float('inf') else "unconnected")

if __name__ == "__main__":
    main()

拓展

这里可能有录友疑惑，while (!que.empty()) 队里里 会不会造成死循环？ 例如 图中有环，这样一直有元素加入到队列里？

其实有环的情况，要看它是 正权回路 还是 负权回路。

题目描述中，已经说了，本题没有 负权回路 。

如图：

img

img

正权回路 就是有环，但环的总权值为正数。

在有环且只有正权回路的情况下，即使元素重复加入队列，最后，也会因为 所有边都松弛后，节点数值（minDist数组）不在发生变化了 而终止。

（而且有重复元素加入队列是正常的，多条路径到达同一个节点，节点必要要选择一个最短的路径，而这个节点就会重复加入队列进行判断，选一个最短的）

在0094.城市间货物运输I 中我们讲过对所有边 最多松弛 n -1 次，就一定可以求出所有起点到所有节点的最小距离即 minDist数组。

即使再松弛n次以上， 所有起点到所有节点的最小距离（minDist数组） 不会再变了。 （这里如果不理解，建议认真看0094.城市间货物运输I讲解）

所以本题我们使用队列优化，有元素重复加入队列，也会因为最后 minDist数组 不会在发生变化而终止。

节点再加入队列，需要有松弛的行为， 而 每个节点已经都计算出来 起点到该节点的最短路径，那么就不会有 执行这个判断条件if (minDist[to] > minDist[from] + value)，从而不会有新的节点加入到队列。

但如果本题有 负权回路，那情况就不一样了，我在下一题目讲解中，会重点讲解 负权回路 带来的变化。

95.城市间货物运输 II

题目描述

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，道路的权值计算方式为：运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

然而，在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时，存在一种情况：**图中可能出现负权回路。**负权回路是指一系列道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴，算法还需检测这种特殊情况。

请找出从城市 1 到城市 n 的所有可能路径中，综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。

城市 1 到城市 n 之间可能会出现没有路径的情况

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。

输出描述

如果没有发现负权回路，则输出一个整数，表示从城市 1 到城市 n 的最低运输成本（包括政府补贴）。如果该整数是负数，则表示实现了盈利。如果发现了负权回路的存在，则输出 “circle”。如果从城市 1 无法到达城市 n，则输出 “unconnected”。

输入示例

1
2
3
4
5
4 4
1 2 -1
2 3 1
3 1 -1 
3 4 1

输出示例

1
circle

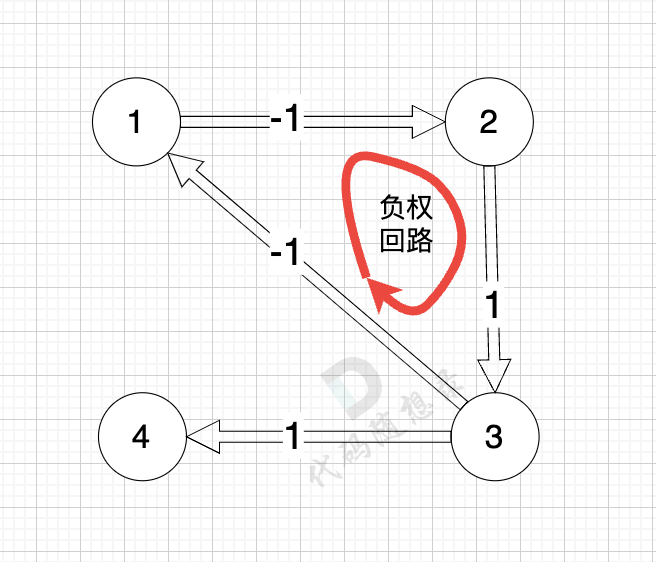
提示信息

路径中存在负权回路，从 1 -> 2 -> 3 -> 1，总权值为 -1，理论上货物运输商可以在该回路无限循环赚取政府补贴，所以输出 “circle” 表示已经检测出了该种情况。

数据范围：

1 <= n <= 1000；
1 <= m <= 10000;

-100 <= v <= 100;

基础思路

之前提到过，当遍历n-1次后，如果没有负权回路，不论再遍历多少次，minDist是不会生成更新的；

所以，我们可以遍历n次，如果第n次minDist需要发生更新，证明就存在负权回路

基础代码

  • 时间复杂度O(NM)
  • 空间复杂度O(M)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
def main():
    n, m = map(int, input().split())
    # graph不使用邻接表
    graph = list()

    for _ in range(m):
        s, t, v = map(int, input().split())
        graph.append([s, t, v])


    minDist = [float('inf')] * (n + 1)
    minDist[1] = 0

    # 遍历n次，第n次时需要判断是否发生了变化
    for i in range(1, n + 1):
        updated = False
        for s, t, v in graph:
            judgeRes = minDist != float('inf') and minDist[s] + v < minDist[t]
            # 第n次判断下就行
            if i == n:
                if judgeRes:
                    # 说明有负权回路(因为第n次又需要更新距离了)
                    print("circle")
                    return
            else:
                if judgeRes:
                    minDist[t] = minDist[s] + v
                    updated = True
        
        # 防止死循环
        if not updated:
            break
    
    print(minDist[-1] if minDist[-1] != float('inf') else "unconnected")


if __name__ == "__main__":
    main()

那，如果使用优化代码（邻接表+队列）的方式，应该怎么写的呢？

优化思路

本题可不可 使用 队列优化版的bellman_ford（SPFA）呢？

上面的解法中，我们对所有边松弛了n-1次后，在松弛一次，如果出现minDist出现变化就判断有负权回路。

如果使用 SPFA 那么节点都是进队列的，那么节点进入队列几次后 足够判断该图是否有负权回路呢？

在 0094.城市间货物运输I-SPFA 中，我们讲过 在极端情况下，即：所有节点都与其他节点相连，每个节点的入度为 n-1 （n为节点数量），所以每个节点最多加入 n-1 次队列。

那么如果节点加入队列的次数 超过了 n-1次 ，那么该图就一定有负权回路。

对于某些复杂的 DAG，一个节点的松弛次数达到 n 是可能发生的，而这并不一定意味着存在负权环。一个更可靠、更被广泛接受的判断标准是当一个节点的松弛次数超过 n 时，才断定存在负权环。

所以本题也是可以使用 SPFA 来做的。 代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <iostream>
#include <vector>
#include <queue>
#include <list>
#include <climits>
using namespace std;

struct Edge { //邻接表
    int to;  // 链接的节点
    int val; // 边的权重

    Edge(int t, int w): to(t), val(w) {}  // 构造函数
};

int main() {
    int n, m, p1, p2, val;
    cin >> n >> m;

    vector<list<Edge>> grid(n + 1); // 邻接表

    // 将所有边保存起来
    for(int i = 0; i < m; i++){
        cin >> p1 >> p2 >> val;
        // p1 指向 p2，权值为 val
        grid[p1].push_back(Edge(p2, val));
    }
    int start = 1;  // 起点
    int end = n;    // 终点

    vector<int> minDist(n + 1 , INT_MAX);
    minDist[start] = 0;

    queue<int> que;
    que.push(start); // 队列里放入起点 
    
    vector<int> count(n+1, 0); // 记录节点加入队列几次
    count[start]++;

    bool flag = false;
    while (!que.empty()) {

        int node = que.front(); que.pop();

        for (Edge edge : grid[node]) {
            int from = node;
            int to = edge.to;
            int value = edge.val;
            if (minDist[to] > minDist[from] + value) { // 开始松弛
                minDist[to] = minDist[from] + value;
                que.push(to);
                count[to]++; 
                if (count[to] == n) {// 如果加入队列次数超过 n-1次 就说明该图与负权回路
                    flag = true;
                    while (!que.empty()) que.pop();
                    break;
                }
            }
        }
    }
    if (flag) cout << "circle" << endl;
    else if (minDist[end] == INT_MAX) {
        cout << "unconnected" << endl;
    } else {
        cout << minDist[end] << endl;
    }
}

以上代码看上去没问题，但提交之后会发现报错了，为什么呢？

例如这组数据：

1
2
3
4
5
6
7
4 6
1 4 3
1 2 1
1 3 1
3 2 -2
2 4 1
3 4 0

如图：

img

img

上面代码在执行的过程中，节点4 已经出队列了，但 计算入度会反复计算 节点4的入度，导致 误判 该图有环。

我们需要记录哪些节点已经出队列了，哪些节点在队列里面，对于已经出队列的节点不用统计入度！

所以，我们这里是一定需要添加inQue来判断哪些节点当前正在队列中

而在没有负权回路的情况，可以不使用inQue（如94题目）

致命缺陷：负权回路的“陷阱” ☠️

现在，我们来看看为什么 in_queue 和入队次数统计是必需的。

考虑一个简单的负权回路：

节点 A 到 B 的权是 3。

节点 B 回到 A 的权是 -5。

这个 A -> B -> A 的回路总权值为 3 + (-5) = -2。

你的代码会发生什么：

  1. 程序从某个起点出发，最终更新了 minDist[A]。A 被加入队列 que。
  2. A 出队，用它更新了邻居 B 的距离 minDist[B]。B 被加入队列 que。
  3. B 出队，用它更新了邻居 A 的距离。因为回路是负权的，所以 minDist[A] 的新值一定比之前更小。于是，A 又被加回了队列！
  4. A 再次出队，它又会去更新 B，使 minDist[B] 变得更小。B 又被加回了队列！

这个过程会无限重复下去。每绕一圈，A 和 B 的 minDist 值就会减 2，永无止境。你的 while que: 循环将永远不会结束，程序会超时（Time Limit Exceeded）。

优化代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class Edge:
    def __init__(self, t, v):
        self.t = t
        self.v = v
 
def main():
    n, m = map(int, input().split())
 
    # graph使用邻接表
    # 需要有个数据结构辅助
    graph = [[] for _ in range(n + 1)]
 
    for _ in range(m):
        s, t, v = map(int, input().split())
        graph[s].append(Edge(t, v))
     
    from collections import deque
 
    que = deque()
    que.append(1)
 
 
    minDist = [float('inf')] * (n + 1)
    minDist[1] = 0
    countInQ = [0] * (n + 1)

    # 记录节点是否在队列中，用于O(1)查询    
    inQue = [0] * (n + 1)
    inQue[1] = 1 # 这行可以不加，因为进入循环后也会被覆盖掉，但更容易理解

    while que:
        s = que.popleft()
        inQue[s] = 0
        for edge in graph[s]:
            t, v = edge.t, edge.v
            if minDist[s] + v < minDist[t]:
                minDist[t] = minDist[s] + v
                
                if inQue[t] == 0:
                    countInQ[t] += 1
                    que.append(t)
                    inQue[t] = 1
										# 对于某些复杂的 DAG，一个节点的松弛次数达到 n 是可能发生的，而这并不一定意味着存在负权环。一个更可靠、更被广泛接受的判断标准是当一个节点的松弛次数超过 n 时，才断定存在负权环。
                    if countInQ[t] > n:
                        print('circle')
                        return
     
    print(minDist[-1] if minDist[-1] != float('inf') else "unconnected")
 
if __name__ == "__main__":
    main()

96.城市间货物运输 III

题目描述

某国为促进城市间经济交流，决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市，通过道路网络连接，网络中的道路仅允许从某个城市单向通行到另一个城市，不能反向通行。

网络中的道路都有各自的运输成本和政府补贴，**道路的权值计算方式为：运输成本 - 政府补贴。**权值为正表示扣除了政府补贴后运输货物仍需支付的费用；权值为负则表示政府的补贴超过了支出的运输成本，实际表现为运输过程中还能赚取一定的收益。

请计算在最多经过 k 个城市的条件下，从城市 src 到城市 dst 的最低运输成本。

输入描述

第一行包含两个正整数，第一个正整数 n 表示该国一共有 n 个城市，第二个整数 m 表示这些城市中共有 m 条道路。

接下来为 m 行，每行包括三个整数，s、t 和 v，表示 s 号城市运输货物到达 t 号城市，道路权值为 v。

最后一行包含三个正整数，src、dst、和 k，src 和 dst 为城市编号，从 src 到 dst 经过的城市数量限制。

输出描述

输出一个整数，表示从城市 src 到城市 dst 的最低运输成本，如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径，则输出 “unreachable”，表示不存在符合条件的运输方案。

输入示例

1
2
3
4
5
6
7
8
9
6 7
1 2 1
2 4 -3
2 5 2
1 3 5
3 5 1
4 6 4
5 6 -2
2 6 1

输出示例

1
0

提示信息

从 2 -> 5 -> 6 中转一站，运输成本为 0。

1 <= n <= 1000；

1 <= m <= 10000;

-100 <= v <= 100;

思路

注意题目中描述是 最多经过 k 个城市的条件下，而不是一定经过k个城市，也可以经过的城市数量比k小，但要最短的路径。

在 kama94.城市间货物运输I 中我们讲了：对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。

节点数量为n，起点到终点，最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。

（如果对以上讲解看不懂，建议详看 kama94.城市间货物运输I ）

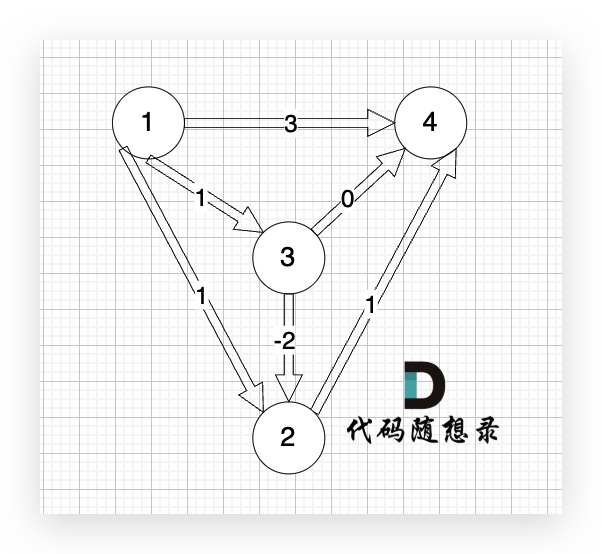
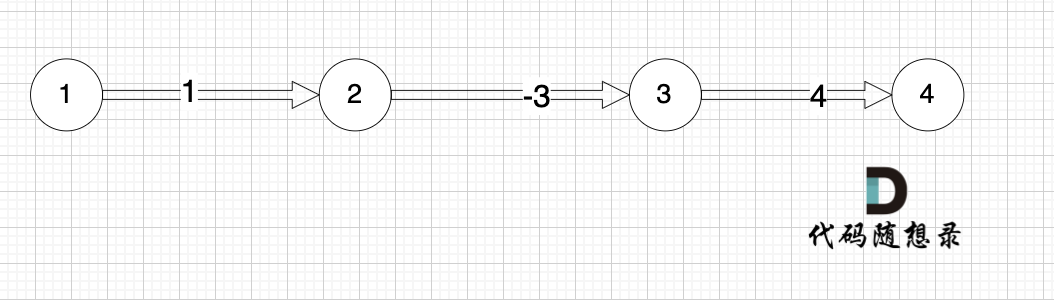
本题是最多经过 k 个城市， 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1，来看这个图：

img

图中，节点1 最多已经经过2个节点 到达节点4，那么中间是有多少条边呢，是 3 条边对吧。

所以本题就是求：起点最多经过k + 1 条边到达终点的最短距离。

对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离，那么对所有边松弛 k + 1次，就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。

注意： 本题是 kama94.城市间货物运输I 的拓展题，如果对 bellman_ford 没有深入了解，强烈建议先看 kama94.城市间货物运输I 再做本题。

理解以上内容，其实本题代码就很容易了，bellman_ford 标准写法是松弛 n-1 次，本题就松弛 k + 1次就好。

以上代码 标准 bellman_ford 写法，松弛 k + 1次，看上去没什么问题。

但大家提交后，居然没通过！

这是为什么呢？

接下来我们拿这组数据来举例：

1
2
3
4
5
6
4 4
1 2 -1
2 3 1
3 1 -1
3 4 1
1 4 3

（注意上面的示例是有负权回路的，只有带负权回路的图才能说明问题）

负权回路是指一条道路的总权值为负，这样的回路使得通过反复经过回路中的道路，理论上可以无限地减少总成本或无限地增加总收益。

正常来说，这组数据输出应该是 1，但以上代码输出的是 -2。

在讲解原因的时候，强烈建议大家，先把 minDist数组打印出来，看看minDist数组是不是按照自己的想法变化的，这样更容易理解我接下来的讲解内容。 （一定要动手，实践出真实，脑洞模拟不靠谱）

接下来，我按照上面的示例带大家 画图举例 对所有边松弛一次 的效果图。

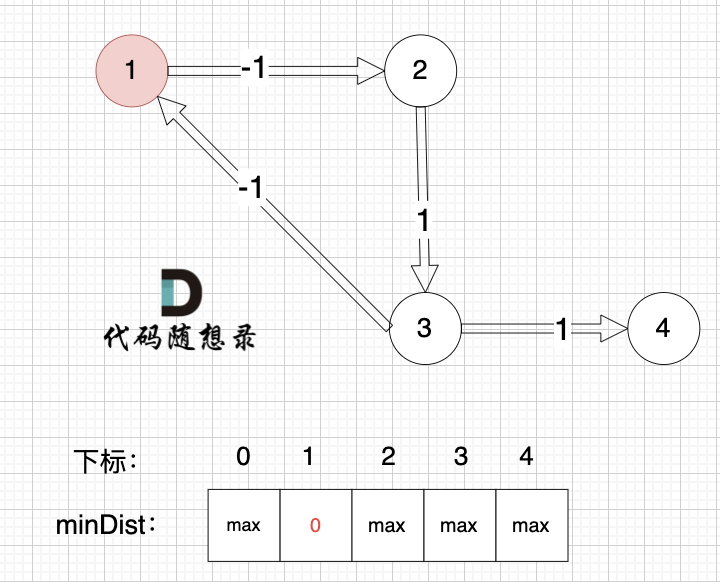
起点为节点1， 起点到起点的距离为0，所以 minDist[1] 初始化为0 ，如图：

img

img

其他节点对应的minDist初始化为max，因为我们要求最小距离，那么还没有计算过的节点 默认是一个最大数，这样才能更新最小距离。

当我们开始对所有边开始第一次松弛：

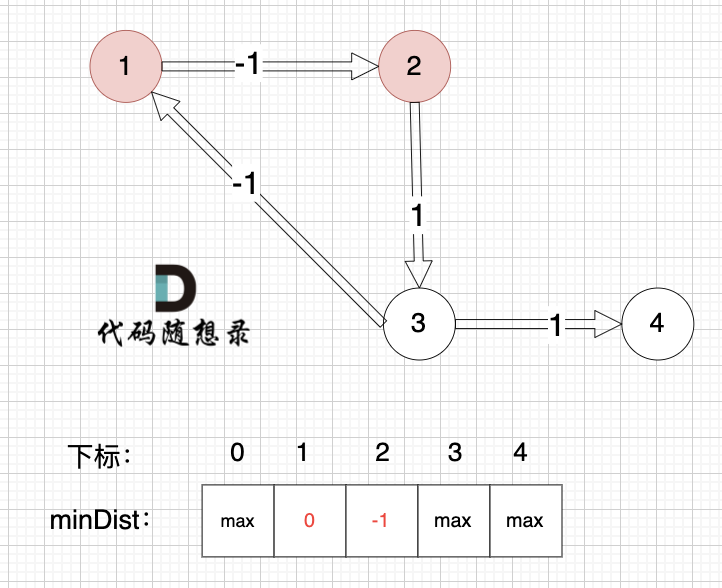
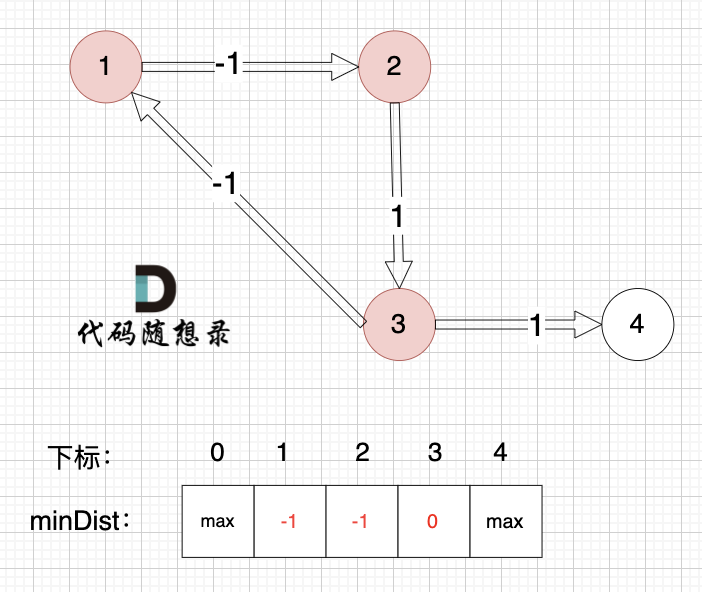
边：节点1 -> 节点2，权值为-1 ，minDist[2] > minDist[1] + (-1)，更新 minDist[2] = minDist[1] + (-1) = 0 - 1 = -1 ，如图：

img

img

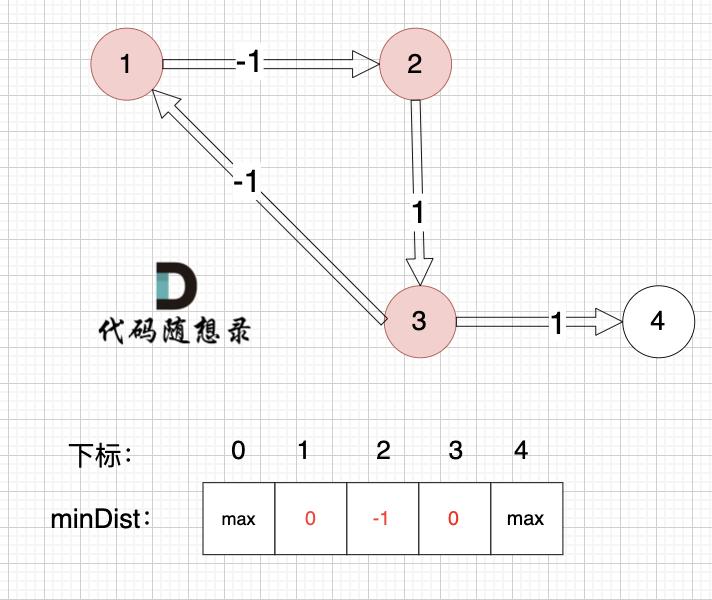
边：节点2 -> 节点3，权值为1 ，minDist[3] > minDist[2] + 1 ，更新 minDist[3] = minDist[2] + 1 = -1 + 1 = 0 ，如图：

img

img

边：节点3 -> 节点1，权值为-1 ，minDist[1] > minDist[3] + (-1)，更新 minDist[1] = 0 + (-1) = -1 ，如图：

img

img

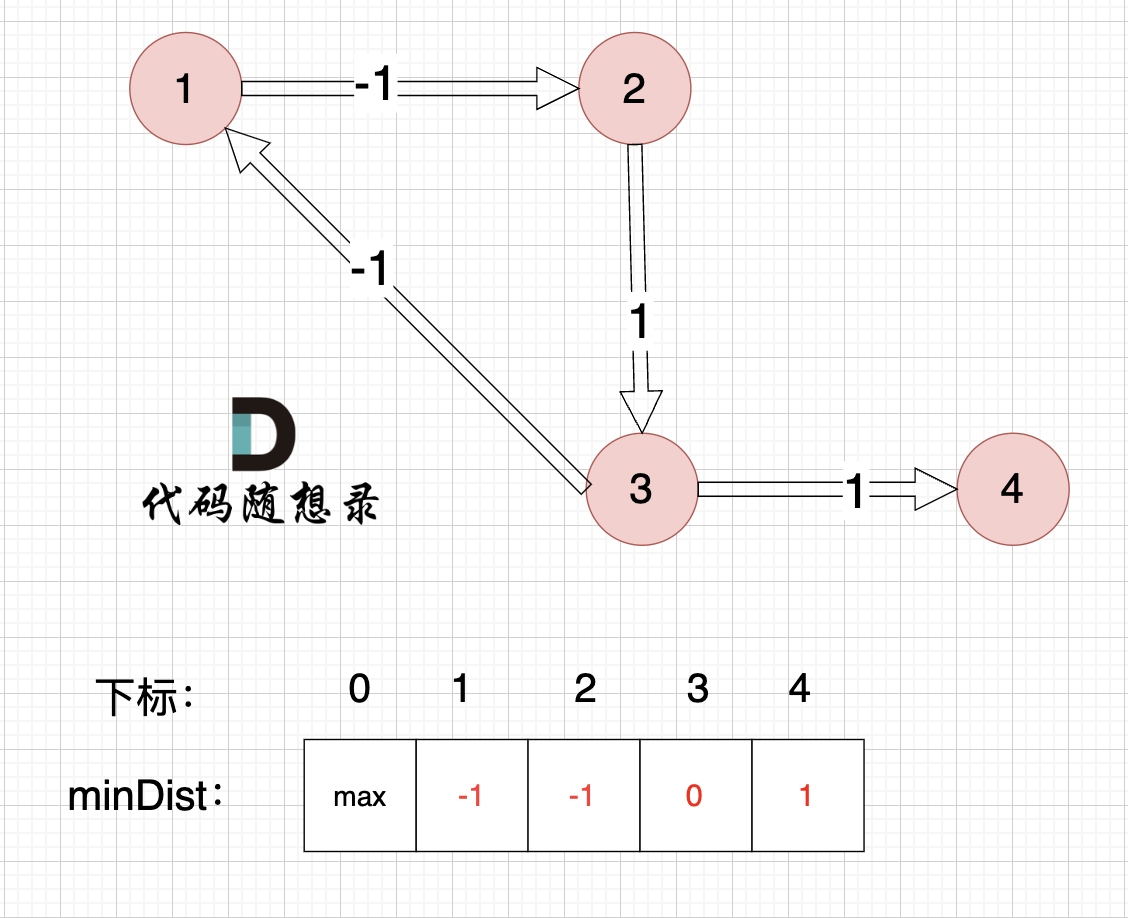
边：节点3 -> 节点4，权值为1 ，minDist[4] > minDist[3] + 1，更新 minDist[4] = 0 + 1 = 1 ，如图：

img

img

以上是对所有边进行的第一次松弛，最后 minDist数组为 ：-1 -1 0 1 ，（从下标1算起）

后面几次松弛我就不挨个画图了，过程大同小异，我直接给出minDist数组的变化：

所有边进行的第二次松弛，minDist数组为 ： -2 -2 -1 0 所有边进行的第三次松弛，minDist数组为 ： -3 -3 -2 -1 所有边进行的第四次松弛，minDist数组为 ： -4 -4 -3 -2 （本示例中k为3，所以松弛4次）

最后计算的结果minDist[4] = -2，即 起点到 节点4，最多经过 3 个节点的最短距离是 -2，但 正确的结果应该是 1，即路径：节点1 -> 节点2 -> 节点3 -> 节点4。

理论上来说，对所有边松弛一次，相当于计算 起点到达 与起点一条边相连的节点 的最短距离。

对所有边松弛两次，相当于计算 起点到达 与起点两条边相连的节点的最短距离。

对所有边松弛三次，以此类推。

但在对所有边松弛第一次的过程中，大家会发现，不仅仅 与起点一条边相连的节点更新了，所有节点都更新了。

而且对所有边的后面几次松弛，同样是更新了所有的节点，说明 至多经过k 个节点 这个限制 根本没有限制住，每个节点的数值都被更新了。

这是为什么？

在上面画图距离中，对所有边进行第一次松弛，在计算 边（节点2 -> 节点3） 的时候，更新了 节点3。

img

img

理论上来说节点3 应该在对所有边第二次松弛的时候才更新。 这因为当时是基于已经计算好的 节点2（minDist[2]）来做计算了。

minDist[2]在计算边：（节点1 -> 节点2）的时候刚刚被赋值为 -1。

这样就造成了一个情况，即：计算minDist数组的时候，基于了本次松弛的 minDist数值，而不是上一次 松弛时候minDist的数值。
所以在每次计算 minDist 时候，要基于 对所有边上一次松弛的 minDist 数值才行，所以我们要记录上一次松弛的minDist。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
def main():
    n, m = map(int, input().split())

    edges = list()

    for _ in range(m):
        s, t, v = map(int, input().split())
        edges.append([s, t, v])
    
    src, dst, k = map(int, input().split())

    minDist = [float('inf')] * (n + 1)
    minDist[src] = 0

    minDistLast = list()
    # 因为最多经过！注意是经过k个城市，所以最多只能有k+1个边
    # 最多遍历k+1次
    for i in range(k + 1):
        # 需要复制一份minDist
        minDistLast = minDist[:]
        updated = False
        for edge in edges:
            s, t, v = edge
            # 使用未更新的minDist进行比较
            if minDistLast[s] != float('inf') and minDistLast[s] + v < minDist[t]:
                minDist[t] = minDistLast[s] + v
                updated = True
        # 防止死循环
        if not updated:
            break
    
    print(minDist[dst] if minDist[dst] != float('inf') else "unreachable")

if __name__ == "__main__":
    main()